Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Problemstellung

In einer Veröffentlichung von 1982 hatte ich vorgeschlagen [1], das Planck'sche Wirkungsquant mit Hilfe von Leuchtdioden im Schülerversuch bestimmen/abschätzen zu lassen, und zwar mittels der Messung der Knickspannung oder Diffusionsspannung U_D, die bei bestimmten Leuchtdioden relativ eng mit dem Bandabstand U_g und damit mit der Photonenenergie E_ph zusammenhängt.

Man erhält also recht direkt - ohne Umweg über die kinetische Energie der Photoelektronen - den Zusammenhang zwischen der Photonenenergie E_ph und der Lichtfrequenz f. Dies und der geringe Preis der Leuchtdioden machen das Verfahren m.E. für Schülerversuche geeignet.

Etwas später erschien in der gleichen Zeitschrift ein sehr ähnlicher Aufsatz [2] von Mitarbeitern der Firma NEVA, die dann auch ein entsprechendes Gerät auf den Lehrmittel-Markt brachten. Heutzutage ist die Grundidee dieser Methode in quasi alle Schulbücher eingedrungen.

Allerdings gab es in den vergangen Jahren auch immer wieder Kritik [3], [4], wenn auch an einer Auswertungsmethode, die ich nicht vorgeschlagen habe. Die Arbeit [4] geht genauer auf die Physik der LEDs ein und schlägt eine ganz andere - kompliziertere - Auswertungsmethode vor, die möglicherweise aber einen genaueren Werte für h liefert. Aus dieser Arbeit habe ich dann auch erfahren, dass schon im Jahre 1974 [5] eine Methode mit Leuchtdioden in einer amerikanischen Zeitschrift vorgestellt wurde.

Die ausführlichen Darlegungen der Arbeit [4], die eigentlich kritisch gemeint waren, möchte ich hier nutzen, um die von mir 1982 vorgeschlagene Auswertungsmethode zu untermauern. Sie erscheint besonders für Schülerversuche geeignet. Sie beruht auf einer anderen Messschaltung als sie häufig von anderen Autoren vorgeschlagen wird.

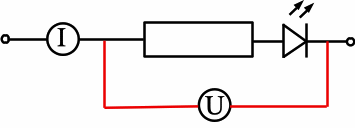
Wesentlicher Punkt der geeigneten Messschaltung ist, dass die in die Kennlinie eingehende Spannung U der Spannungsabfall an der Reihenschaltung von LED und Vorwiderstand R ist. Wenn die Stromstärke auf 0 herunter geregelt ist, verschwindet auch der Spannungsabfall an R, und die gemessene Spannung ist nur noch der gesuchte Spannungsabfall an der LED.

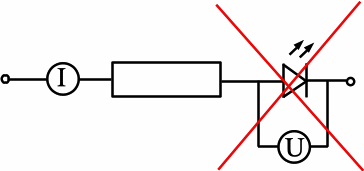ungeeignete Messschaltung zur h-Bestimmung

Auswertungsmethode (Extrapolationsmethode)

Bei Stromfluss durch eine LED fallen in der Sperrschicht des p-n-Übergangs Elektronen aus dem Leitungsband der n-Zone in das Valenzband der p-Zone und rekombinieren dort mit Löchern. Die Photonenenergie E_ph entspricht damit recht gut dem Bandkantenabstand U_g. Sie wird also durch U_g gemessen.

Wesentlich für die hier und 1982 vorgeschlagene Auswertungsmethode ist, dass der üblicherweise in Steckerbausteinen der Schule vorgesehene Schutzwiderstand von ca. 330 Ohm zur Messung der Knickspannung mit genutzt wird. Er bewirkt eine Linearisierung der I-U-Kennlinie. Es wird also gerade das "Hochstromverhalten" für LED-Ströme bis typisch 20 mA (oder 100 mA bei IR-LEDs) vermessen. Durch Extrapolation in den "Niederstrombereich" erhält man dann einen reproduzierbaren Wert für die Knickspannung U_D bzw. U_g . Trotz - im Idealfall kleiner - möglicher Abweichungen vom Bandkantenabstand zwischen Valenzband und Leitungsband wird diese Knickspannung als Maß dafür genommen. Weder eine Messung von U_D mittels des schleifenden Eintritts der Kennlinie in die U-Achse noch eine Messung der Durchflussspannung mit dem dafür vorgesehenen Messbereich des Multimeters liefern meiner Erfahrung nach wirklich reproduzierbare Werte. M.E. kann man höchstens durch Zufall zu vernünftigen Werten kommen, wenn man eine Spannung sucht, bei der die LED gerade zu leuchten beginnt. Damit zusammenhängende Verfahren sind es, die in der Literatur mit Recht kritisiert werden.

Begründung der Extrapolationsmethode

Betrachten Sie folgende Ersatzschaltung:

Danach teilt sich die Batteriespannung U auf in die Spannung U_pn am p-n-Übergang, einen Spannungsabfall U_i am inneren Widerstand R_i der LED und den Spannungsabfall R·I am Schutzwiderstand R:

(1) U = U_pn + U_i + I·R

I und U können leicht gemessen werden. Für I gilt die Shockley-Gleichung des p-n-Übergangs (vgl. z.B. [4] ):

(2) I = I₀ ·exp (U_pn /U_th - 1) , wobei U_th = n· k_B·T/e mit der Boltzmann-Konstanten k_B. Der Idealitätsfaktor (Qualitätsfaktor, Emissionsfaktor) n hängt von der LED ab. Ein typischer Wert nach [4] ist n = 1,62.

Noch kann man nicht erkennen, wie hier die Knickspannung U_D bzw. der Bandkantenabstand U_g ins Spiel kommen soll. Bei Zimmertemperatur (300 K) ist U_th = 1,62·0,026 V = 0,042 V. Bei Spannungen U_pn in der Größenordnung von 2 V kann dann die 1 in (2) vernachlässigt werden, und es gilt in guter Näherung:

(2') I = I₀ exp (U_pn /U_th)

I₀ heißt Sättigungsstromstärke für die Sperrrichtung (Sättigungssperrstrom), die von verschiedenen Diodeneigenschaften abhängt, z.B. der Querschnittsfläche des p-n-Übergangs. Für sie gilt nach [4]:

(3) I₀ = a · exp (-U_g/U_th) . So kommt endlich der Bandabstand U_g ins Spiel! Wir wollen uns noch eine Größenvorstellung von a verschaffen. Nach [4] gilt für eine typische grüne LED: I₀ = 1,5·10^-21 A, U_g = 1,9 V. Also:

(3') a = I₀ / exp (-U_g/U_th) = 1,5·10^-21 A / exp( -42,86) = 1,5·10^-21 A / 2,2·10^-20 = 0,6·10^-1 A

Entsprechend gilt für eine typische IR-LED mit I₀ = 2,2·10^-11 A, U_g = 1,0 V:

(3") a = I₀ / exp (-U_g/U_th) = 2,2·10^-11 A / exp( -26,2) = 2,2·10^-11 A / 4,5·10^-11 = 0,5 A

Also ist a grob in der Größenordnung von 0,1 A. Wegen des Logarithmus in der folgenden Gleichung (1') kommt es auf den genauen Wert nicht an.

Es gilt also

(2") I = a·exp ((U_pn -U_g)/U_th)

Wir lösen nach dem gesuchten U_pn in Gl. (1) auf: U_pn = U_th ln(I/a ) + U_g. Eingesetzt in (1) folgt:

(1') U = U_th ln(I/a ) + U_g + U_i + I·R

Bei einem Innenwiderstand in der Größenordnung von 1 Ohm [4] ist U_i gegenüber I·R (R typ. 330 Ohm) vernachlässigbar.

(a) Bestimmen wir die Steigung des I-U-Graphen: dU/dI = R + U_th/I . Schon bei I = 10 mA und U_th = 0,042 V ist der zweite Term vernachlässigbar gegenüber R = 330 Ohm.

Wir haben so nachgewiesen, dass sich für größere Stromstärken I eine konstante Steigung R ergibt, also ist dort die I-U-Kennlinie in guter Näherung ein Geradenstück. Die Linearisierung durch den Widerstand R ist verstanden.

(b) Wenn U_th = 0,042 V und a in der Größenordnung von 0,1 A ist bei I in der Größenordnung von 10 mA, ist der erste Term in der Größenordnung von -0,1 V. Andere Fehlerquellen liegen in gleicher Größenordnung, d.h. auch dieser Term ist vernachlässigbar, insbesondere im Vergleich zu U > 3 V. Damit erhalten wir in brauchbarer Näherung für die I-U-Funktion eine Geradengleichung:

Diese Gleichung begründet die Extrapolationsmethode.

Sollte für andere LEDs der hier wegdiskutierte Term größer sein, so ist doch zu berücksichtigen, dass er wegen des Logarithmus nur wenig von der Stromstärke abhängt, also als quasi konstant angesehen werden kann. Dann wäre die gemessene Knickspannung gegenüber U_g um diese Quasi-Konstante verfälscht. Auch das wäre nicht schlimm für die Messung von h, da eine solche Konstante in die Steigung des U_g-f-Graphen nicht eingeht, wenn nur diese Konstante für alle LEDs etwa den gleichen Wert hat. Messung an realen LEDs zeigt, dass man im Rahmen des Möglichen keine Bedenken haben muss.

Das heißt: Wenn die Kennlinie im Hochstrombereich (5 mA - 20 mA) vermessen wird, schneidet die extrapolierte Gerade die U-Achse bei einer Spannung, die bis auf wenige zehntel V Fehler mit dem Band-Abstand U_g übereinstimmt.

Eine höhere Genauigkeit kann man nicht erwarten, da ja auch Donator- und Akzeptorzustände eine Rolle spielen, die um wenige zehntel eV von den Bandkanten verschieden sind.

Nur mit ausgewählten LEDs sind alle diskutierten Näherungen gut erfüllt. Dann funktioniert das Verfahren; sicher aber nicht mit den modernen superhellen LEDs, die durch indirekte Bandübergänge charakterisiert sind, was sich auch in der größeren Flussspannung zeigt. Aber, wenn man geeignete LEDs ausgewählt hat: dann ergeben sich immer reproduzierbare Werte.

Für einen Schülerversuch halte ich diese Methode für sehr geeignet, weil er mit geringsten Kosten in parallelen Arbeitsgruppen durchgeführt werden kann und weil er (in gewisser Weise) direkter den Zusammenhang zwischen Photonenenergie und Frequenz liefert als der Photoeffekt.

Was sagt man den Schülern?

Im einfachsten Fall beschränkt sich der Lehrer auf die Informationen:

Unter geeigneten Umständen fallen in der Sperrschicht der LED Elektronen der n-leitenden Zone in Löcher der p-leitenden Zone. Dabei wird (u.a.) jeweils die Energiedifferenz e·U_g zwischen Elektronen und Löchern in Form eines Photons ausgesandt. Damit dies möglich wird, muss den Elektronen durch die angelegte Spannung erst eine Energie von mindestens dem Wert e·U_g (gemessen durch e·U_D) zugeführt werden. Erst von da an können Elektronen zugleich einen Strom transportieren und Photonen abgeben.

Wegen verschiedener Effekte ist diese Situation aber schwer zu erkennen. Deshalb liegt die Extrapolationsmethode mittels des geraden Teils der U-I-Kennlinie nahe.

Literatur

[1] H. Hübel: Leuchtdioden: annähernd monochromatische Lichtquellen für physikalische Schülerversuche zur Gitterbeugung und zum Planckschen Wirkungsquant, Praxis der Naturwissenschaften, Teil Physik, 31 (1982), Heft 3, S. 82

[2] H. Müller: Schulversuche mit Leuchtdioden, Praxis der Naturwissenschaften, Teil Physik, 39 (1990), Heft 7, S. 33-39

[3] F. Herrmann, D. Schätzle,"Question #53. Measuring Planck's constant by means of an LED", Am. J. Phys. 64 (12), 1448 (1996)

[4] R. Morehouse, "Answer to Question #53. Measuring Planck's constant by means of an LED", Am. J. Phys. 66 (1), 12 (1998)

[5] P.J. O'Connor and L.R. O'Connor, "Measuring Planck's constant using a light emitting diode", Phys. Teach. 12, 423 - 425 (1974)