(1) Ein klassisches Teilchen soll sich kräftefrei längs einer Strecke der Länge 2a  hin und her bewegen können. An den Enden dieser Strecke sorgen starke Kräfte dafür, dass das Teilchen reflektiert wird. Dem entspricht also ein Potenzialgebirge oder Potenzialtopf, dessen Boden überall 0 ist, mit unendlichen Wänden an den Rändern. Einem Quantenteilchen kann man die gleiche Potenzialfunktion Wpot(x) vorgeben. Aber es ist dann sinnlos von einer Bewegung oder gar einer Hin- und Herbewegung zu sprechen, weil das Quantenteilchen ja dann zu allen Zeiten gleichzeitig Ort und Geschwindigkeit (Impuls) als Eigenschaften haben müsste, was wegen der Komplementarität ausgeschlossen ist. Man kann dann nur noch von zwei klassisch denkbaren (Bewegungs-)Möglichkeiten sprechen. Wenn zwischen diesen nicht durch eine Messung unterschieden wird, kommt es zur Interferenz. Es sind dann Stellen zu beobachten, in deren Umgebung das Teilchen mit hoher Wahrscheinlichkeit (rot) zu finden ist (Maxima), und Stellen, in deren Nähe das Teilchen mit quasi verschwindender Wahrscheinlichkeit zu finden ist. In Analogie zu stehenden Wellen heißen die Maxima hier auch "Bäuche" und die Minima "Knoten". Bei bestimmten Energien ist das Interferenzbild stationär, d.h. ortsfest. Dann befindet sich das Teilchen in einem "stationären Zustand". Die Energie E ist dann eine be-stimmte Eigenschaft des Teilchens, ein "Energie-Eigenwert", weil sie dem Teilchen im Potenzialkasten wirklich zueigen ist. Jede Energiemessung im gleichen Zustand liefert dann die gleiche Energie. Es gibt andere Zustände mit un-be-stimmter Energie. Energiemessungen im jeweils gleichen Zustand liefern dann streuende Messwerte; es gibt dann in der Regel kein stationäres Interferenzbild bzw. keine stationäre Wahrscheinlichkeitsverteilung. In stationären Zuständen mit konstanter (Gesamt-)Energie E sind kinetische und potenzielle Energie un-be-stimmt. Würde man sie immer wieder im gleichen stationären Zustand messen, erhielte man streuende Messwerte. Wiederum: Für Quantenteilchen im Potenzialkasten ist "Bewegung" ein sinnloser Begriff.

(2) Manchmal wird gefragt, wie es denn möglich ist, dass ein hin und her laufenden Quantenteilchen über einen Knoten hinweg kommt, wenn es sich dort nie aufhalten kann. Tatsächlich ist eine solche Bewegung für ein Quantenteilchen eine sinnlose Vorstellung. Knoten und Bäuche für die Wahrscheinlichkeitsverteilung für den Nachweis des Teilchens gibt es nur in stationären Zuständen mit be-stimmter (Gesamt-)Energie. Für solche Quantenteilchen ist "Bewegung" ein sinnloser Begriff. Mit nicht-stationären Zuständen kann man eine Situation konstruieren, die - wenigstens kurzzeitig - einem laufenden klassischen Teilchen ähnelt ("laufendes Wellenpaket"). Auch für Quantenteilchen in einem solchen Zustand bleibt aber "Bewegung" streng genommen ein sinnloser Begriff.

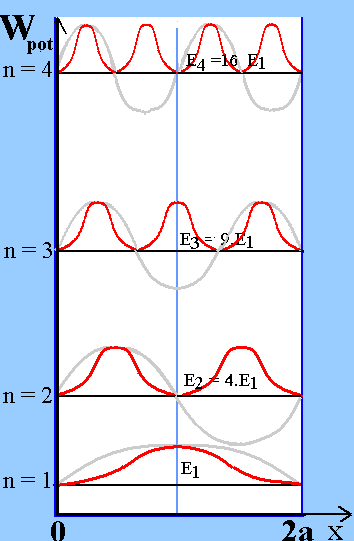
(3) Energiewerte und Wahrscheinlichkeitsverteilung für ein Quantenteilchen im Potenzialkasten lassen sich auch auf Schulniveau leicht mit der Schrödinger-Gleichung berechnen, vereinfacht sogar durch das "Einpassen von stehenden Wellen in den Potenzialkasten". Es stellt sich  eine einfache Gesetzmäßigkeit En = E1·n2  heraus, wobei E1 = h2/(32·a2·m)  und n ε N mit der Länge 2·a des Potenzialkastens. m ist dabei die Teilchenmasse, h das Plancksche Wirkungsquant. Bemerkenswert ist, dass die tiefstmögliche Energie E1 , die "Grundzustandsenergie", von 0 verschieden ist, anders als man das für ein klassisches Teilchen erwartet hätte. Mit zunehmender Quantenzahl n wachsen die erlaubten Energien quadratisch mit n. Die Lokalisierung des Teilchens auf den Raum des Potenzialkastens ist mit "diskreten Energien" (diskret = durch Energielücken getrennt) für die stationären Zustände verbunden, wie es auch in anderen "gebundenen Zuständen" der Fall ist. Prominentestes Beispiel ist das eine Elektron, das im Coulombfeld eines H-Atom-Kerns eingefangen ist.

(aktualisiert 2012)