Ein klassisches Teilchen kann potenzielle und kinetische Energie, E_pot und E_kin, besitzen. Ihre Summe bildet die Gesamtenergie E. Die Abhängigkeit der potenziellen Energie vom Ort x heißt Potenzialfunktion W_pot(x). Bei klassischen Teilchen gilt für ihre potenzielle Energie an einem Ort x stets E_pot = W_pot(x).

Das Potenzialgebirge von Abbildung 2 enthält einem Potenzialtopf und einen Potenzialwall, der oft auch Potenzialschwelle oder Potenzialbarriere genannt wird.

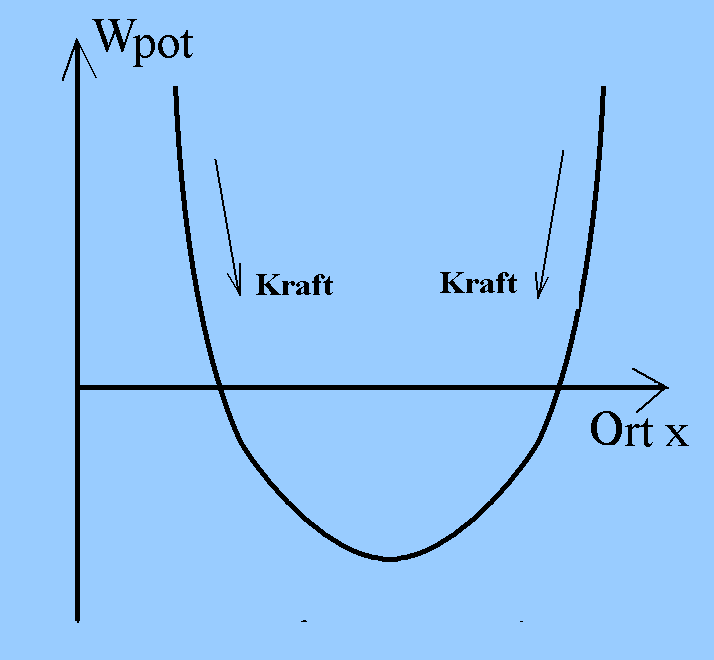
Im Potenzialkasten mit geneigten Wänden (Abb. 1) erfahren Teilchen - klassisch gesprochen - eine rücktreibende Kraft (den Hang abwärts), wenn sie sich der Wand annähern. Dem entspricht sozusagen ein "Drang, die potenzielle Energie zu verringern". Je steiler die Wand, desto größer ist die Kraft. Im Grenzwert einer senkrechten Wand ist die Kraft beliebig groß. Durch den Potenzialanstieg werden die Teilchen im Inneren festgehalten wie in einem Potenzialkasten. An der tiefsten Stelle aber erfahren die Teilchen nach der Potenzialfunktion der Abbildung 1 keine Kräfte.

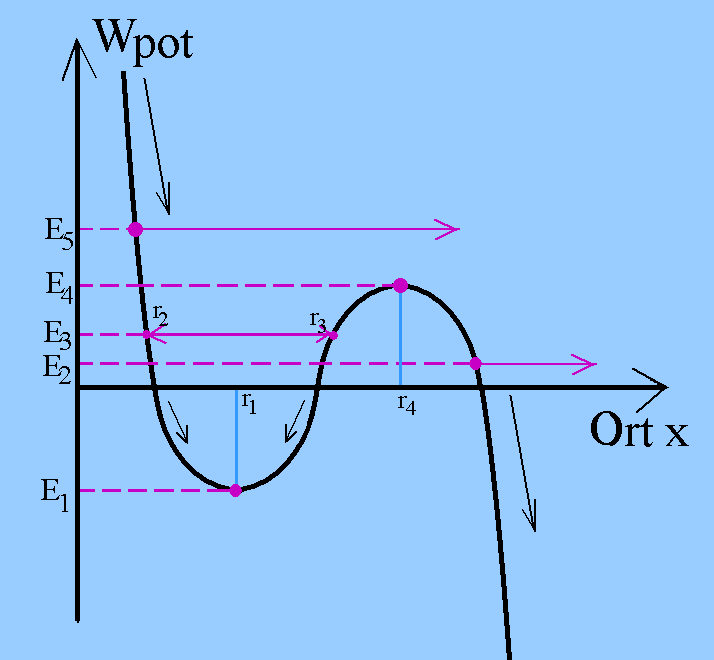Abb. 1: Die Potenzialfunktion Wpot(x) lehrt bei klassischen Teilchen, welche Kräfte wirken, insbesondere, welche Richtung sie haben. Kräfte sind im Graphen der Potenzial- funktion immer hangabwärts gerichtet.	Abb. 2: Bei dieser Potenzialfunktion Wpot(x) wirken auf klassischen Teilchen anziehende und abstoßende, bindende oder gar keine Kräfte, die zu Gleichgewichtslagen, zu peri- odischen Bewegungen oder zur Abstoßung führen.

In der Abbildung 2 kann man die gleiche Regel anwenden: Kräfte auf klassische Teilchen sind im Potenzialgebirge immer hangabwärts gerichtet. Deswegen erleiden klassische Teilchen mit unterschiedlichen Energien unterschiedliche Schicksale:

Gesamtenergie E1: Das klassische Teilchen erfährt keine Kräfte, sondern bleibt am Ort x = r1 ("stabiles Gleichgewicht"). E2: Das Teilchen kann seine potenzielle Energie verringern und gewinnt dabei kinetische Energie, d.h. es wird vom Zentrum (x = 0) immer schneller weg beschleunigt. E3: Das Teilchen erfährt nach links wie nach rechts gerichtete Kräfte. Wegen seiner Trägheit bewegt es sich über den Punkt (r1) kräftefrei hinweg. Es pendelt ständig zwischen den Radien r2 und r3. An den Umkehrpunkten hat es ausschließlich potenzielle Energie. An der Stelle des Potenzialminimums hat es maximale kinetische Energie. E4: Das Teilchen erfährt keine Kräfte, sondern bleibt am Ort x = r4 ("instabiles Gleichgewicht"). E5: Das Teilchen erfährt überall vom Zentrum (x = 0) weg gerichtete Kräfte. Es kann seine potenzielle Energie überall verringern und gewinnt dabei kinetische Energie. Es entfernt sich vom Zentrum.

Der Energieerhaltungssatz sorgt dabei - im klassischen Fall - für das Wechselspiel von kinetischer und potenzieller Energie.

Die Quantenphysik lehrt hingegen: Kein System kann nach der Un-be-stimmtheitsrelation zugleich be-stimmte Gesamtenergie und be-stimmte potenzielle Energie oder be-stimmte Gesamtenergie und be-stimmte kinetische Energie oder be-stimmte potenzielle Energie und be-stimmte kinetische Energie zugleich haben (siehe Unbestimmtheitsrelation). Die drei Energien sind komplementär zueinander, und die Potenzialfunktion Wpot(x) hat dort nur formale Bedeutung. Sie geht aber in die Schrödinger-Gleichung ein und hat so doch bedeutenden Einfluss auf die möglichen Werte der Gesamtenergie E und auf die Wahrscheinlichkeit, ein Teilchen in der Nähe einer Stelle x zu finden.

Weil in der Quantenphysik also ein Energieerhaltungssatz mit kinetischer und potenzieller Energie nicht anwendbar ist, werden klassische Argumente ungültig, die auf dem Energieerhaltungssatz beruhen. Deshalb ist es hier durchaus möglich, dass - entsprechend Abb. 2 - ein Teilchen mit der Energie E₂ in den Potenzialwall eindringen und ihn sogar durchdringen kann (s. Tunneleffekt)