

|
|
Bragg-Reflexion korpuskular
und wellentheoretisch
- Modellversuch mit Ultraschall |
In einer Veröffentlichung von 1981 wurde vom Autor ein Modellversuch zur Bragg-Streuung von Ultraschall an einem Modellkristall vorgestellt. Auf einer Tagung 1988 wurde dann eine Methode aufgezeigt, den Versuch zu einer induktiven Herleitung der Bragg-Gleichung einzusetzen, ein Weg, der m.E. Wesentliches klarer herausstellt als die übliche alleinige rechnerische Herleitung. Voraussetzung für diesen Weg war eine recht einfache Vorrichtung, die für eine genaue Einhaltung des Reflexionsgesetzes für die Ultraschallwellen sorgte. Diese Methode wird hier noch einmal zusammengefasst und zugleich in einen anderen Rahmen gestellt.
 |
 |
| Abb. 1: Modellkristall mit Netzebenenabstand d = 1,5 cm | Abb. 2: Gesamtanordnung: Rechts der Sender, der mit einem Funktionsgenerator zu verbinden ist, links der Empfänger mit dem Wechselspannungsverstärker, der mit einem beliebigen Wechselspannungsvoltmeter verbunden wird. Das Foto entstand im Unterricht an der Deutschen Schule Algarve in Silves (Portugal) |
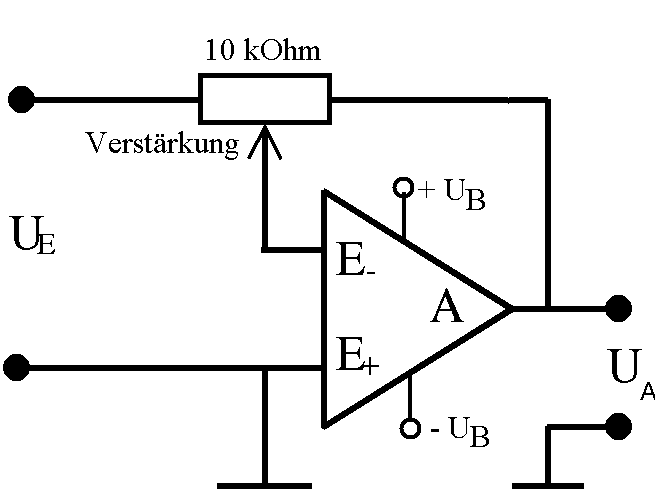
Im Zentrum steht ein Modellkristall aus Holzperlen, der schon 1981 beschrieben wurde (Abb. 1). Wesentlich für das Gelingen des Versuchs sind wohl die regelmäßig angeordneten "Perlenträger", für die damals Fahrradspeichen eingesetzt wurden. An der Uni München wurde damals ein modifzierter Nachbau eingesetzt, bei dem auf die Holzperlen verzichtet wurde. Aus didaktischen Gründen würde ich diese aber in der Schule beibehalten. Als Ultraschall-Sender und -Empfänger wurden Bauteile von Murata eingesetzt, die z.B. von Reichelt electronic für wenige Euros erhältlich sind (UST-40T). Mit Hilfe von Spiegeln wird ein Parallelstrahlbündel erzeugt, das möglichst den ganzen Kristall erfasst. Damals konnte man billige Plastikspiegel von ca. 12 cm Durchmesser als Solar-Zigarettenanzünder erwerben mit einer Brennweite von wenigen cm. Notfalls lassen sich auch Badezimmerspiegel aus dem Baumarkt verwenden, die leider eine größere Brennweite haben. Der Ultraschall-Lautsprecher wird direkt aus einem Funktionsgenerator mit 41 kHz versorgt. Das Ultraschall-Mikrophon könnte man direkt mit einem Oszilloskop verbinden. Wir haben aber mit Hilfe eines Operationsverstärkers LF256 (oder TL81) einen kleinen Wechselspannungsverstärker direkt hinter das Mikrophon gebaut (Abb. 3). Sein Ausgang kann dann mit einem beliebigen Wechselspannungsvoltmeter verbunden werden. Um Netzbrumm zu vermeiden, muss der Eingang bzw. das Mikrophon niederohmiger gemacht werden, z.B. durch Parallelschalten eines 10 kOhm-Widerstands. Die Vorrichtung zur Einhaltung des Reflexionsgesetzes ist in der Abb. 4 ersichtlich. Ähnlich einem "Storchschnabel" markieren Lineale die Richtungen von einfallendem und austretendem US-Bündel entlang der Seiten eines Parallelogramms. Die Diagonale bildet das Lot auf einer Netzebene und ist mit dem Kristallträger (Achse) fest verbunden, während sich die Parallelogramm-Seiten bewegen können. Die dem Kristall gegenüberliegende Seite des Parallelogramms gleitet, irgendwie geführt, auf der Diagonalen. Der Kristall sitzt auf einer Achse, die drehbar fixiert ist. Wenn jetzt einer der Arme gedreht wird, muss sich auch der Kristall und eventuell der zweite Arm mitdrehen.
 |
 |
| Abb. 3: Ultraschall-Empfänger mit nachgeschalteten Wechselspannungsverstärker | Abb. 4: Anordnung zur Einhaltung des Reflexionsgesetzes |
 |
 |
| Abb. 5a: Schaltung des Wechselspannungsverstärkers mit
dem Operationsverstärker LF256 oder TL81 (invertierende Schaltung). Bei uns werden die beiden Betriebsspannungen durch 2 Batteriepacks bereitgestellt. |
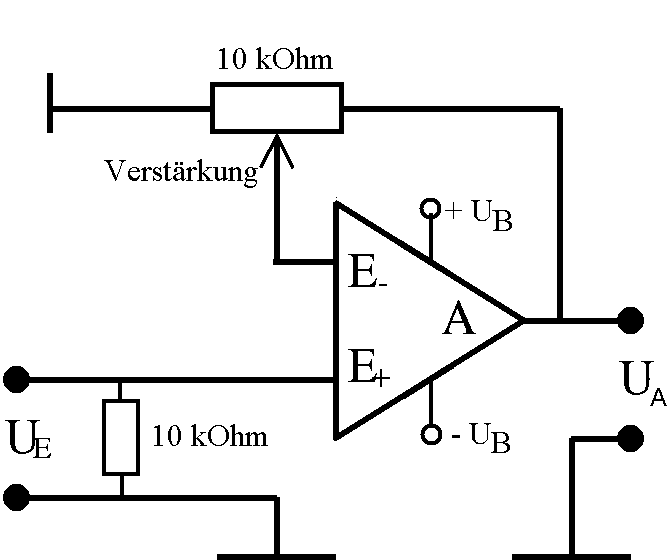
Abb. 5b: Schaltung des Wechselspannungsverstärkers mit
dem Operationsverstärker LF256 oder TL81 (nicht invertierende Schaltung). Hier muss der Eingangswiderstand künstlich reduziert werden. |
Man geht folgendermaßen vor:
1. Demonstration des Reflexionsgesetzes für Ultraschall
Der Kristall wird durch eine ebene Fläche (z.B. Seitenfläche eines quaderförmigen Kartons) ersetzt. Die Achse liegt in der refektierenden Fläche; diese ist senkrecht zur Diagonalen. Ganz gleich, welcher Einfallswinkel gewählt wird, das Mikrophon registriert immer starke Ultraschall-Strahlung: Reflexion von Ultraschall. Wird der Reflektor entfernt, bleibt diese aus.
2. Das Phänomen der Bragg-Reflexion
Der Modellkristall wird installiert. I.A. erhält man jetzt keinen nennenswert reflektierten US-Strahl. Das geschieht nur bei ganz bestimmten Glanzwinkeln: Bragg-Reflexion, aber keine Reflexion.
3. Quantitative Untersuchung der Bragg-Reflexion
Die Positionen der der Achse gegenüberliegenden Ecke werden markiert (Abb. 6b: P1, P2, P3, ...). Bei den verwendeten Dimensionen (λ = ca. 8 mm, d = 1,5 cm) können 3 Ordnungen beobachtet werden. Die Längen der jeweiligen Diagonalen sind ganzzahlige Vielfache einer kleinsten Länge k. Dadurch sind die Winkel festgelegt. Die weitere Diskussion verläuft dann folgendermaßen:
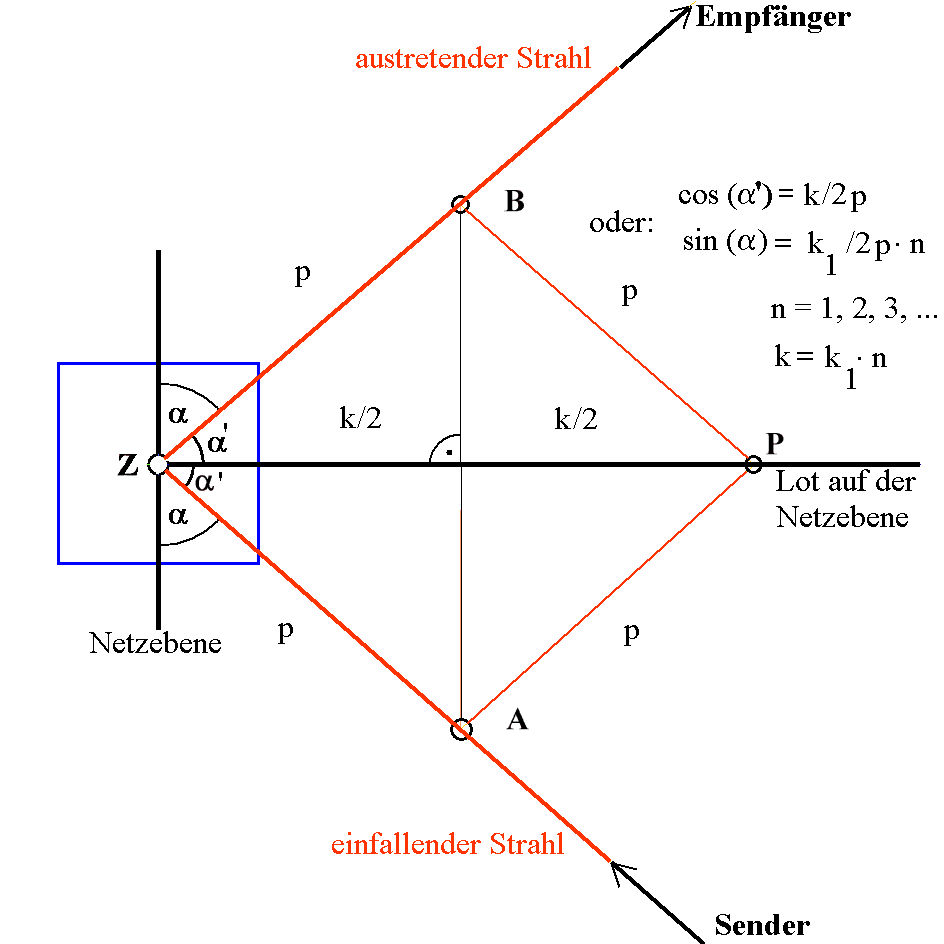
Anders als im Teilchen- oder Wellenbild kann zunächst allein die Geometrie genutzt werden. Es gilt dann nach Abb. 6a, wenn p die Länge Parallelogramm-Seite ist:
sin(α) = (k·n/2)/p = k·n/(2·p) = 1/2 k/p n (n = 1,2,3, ...)
 |
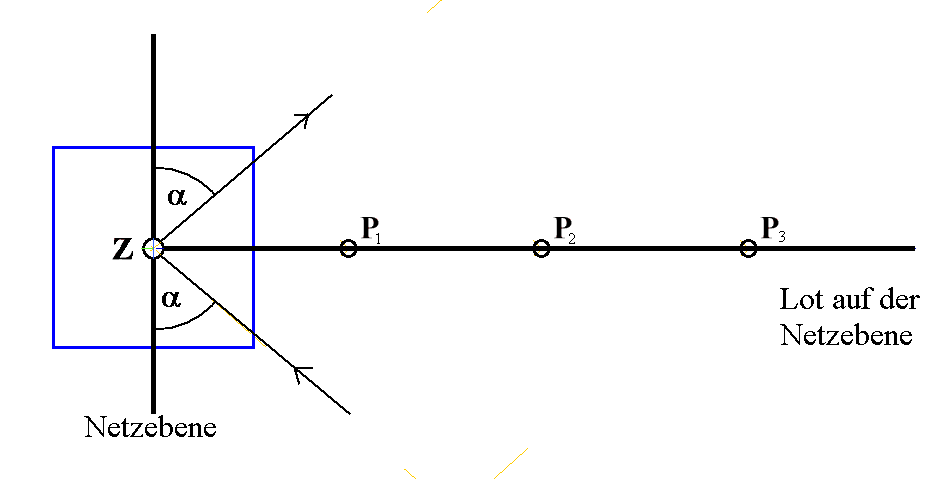 |
| Abb. 6a: Geometrie der Bragg-Streuung | Abb. 6b: Das ergibt sich für die Parallelogramm-Ecken bei den Glanzwinkeln |
Damit ist also eine phänomenlogische Bedingung für die Glanzwinkel α gewonnen. Nur bei solchen Glanzwinkeln findet Bragg-Reflexion statt. Es ist anschaulich klar, dass es eine geometrische Bedingung entsprechend Abb. 6a für die möglichen Glanzwinkel α gibt. Das motiviert den Versuch einer physikalischen Deutung, bei Ultraschall - naheliegend - zunächst mit dem Wellenbild.
4. Deutung durch Kristallgitter-Beugung von Wellen (Abb.7):
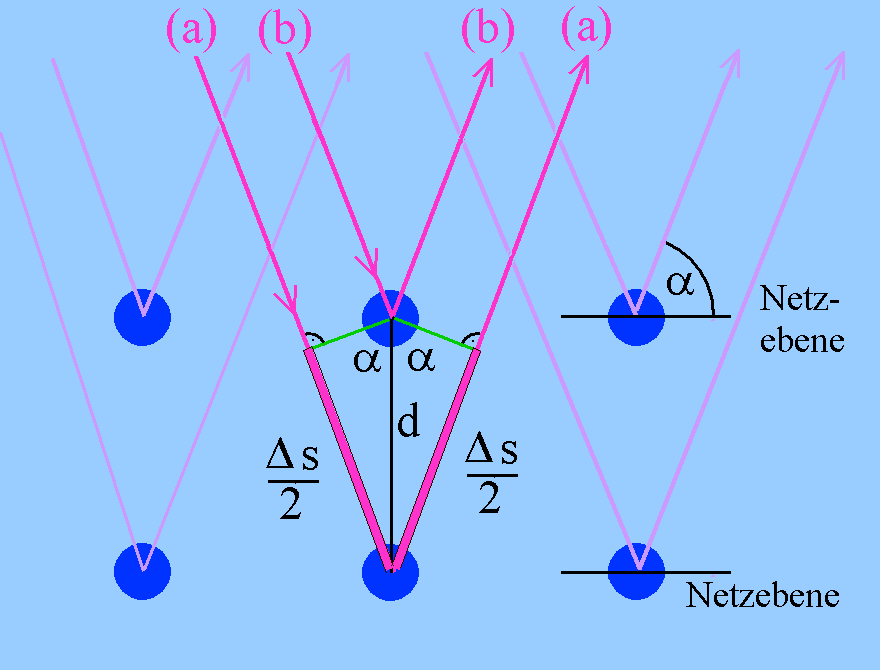
Abb. 7: Übliche "Wellentheorie" der Bragg-Streuung |
Die Wellen werden an "Atomen" (Streuzentren) gebeugt. Sie
breiten sich nach der Streuung in alle Richtungen aus, u.a. in
Richtung eines der vermuteten Maxima. Wenn der Gangunterschied Δs
(Wegunterschied) zwischen zwei an benachbarten Atomen gebeugten
Wellen [(a) und (b)] gerade ein ganzzahliges Vielfaches der
Wellenlänge λ beträgt, verstärken sich die beiden Wellen, es
entsteht ein Maximum (Maximum, wenn Δs = λ · n (n ε
Z)). Δs setzt sich hier aus zwei Anteilen zusammen! Dann
verstärken sich auch alle übrigen gleichgerichteten Strahlen
paarweise; es sind im Prinzip alle Atome einer Netzebene und alle
Netzebenen beteiligt. [ Hier geht die Periodizität
des Gitters ein.]
Mit dem Glanzwinkel α erhalten Sie:
Bei bekanntem Netzebenenabstand d können Sie mit dieser Beziehung die Wellenlänge λ berechnen, bei bekannter Wellenlänge λ erhalten Sie den Netzebenenabstand d. Das entspricht dem Versuchsergebnis. Es ist identifiziert. k/p = λ/d . Es ist geklärt, weshalb nur bestimmte Glanzwinkel auftreten. Wieviele, ergibt sich ebenfalls daraus: Wegen /sin(α)/ <= 1 muss λ/d · n/2 <= 1 sein. Daraus ergibt sich nmax <= 2·d/λ. Bei uns also wegen d = 1,5 cm und λ = ca. 0,8 cm: nmax <= 3.
|
5. Übergang zur Quantenphysik
Historisch war Bragg-Streuung an den Kristallgittern realer Kristalle der Nachweis eines "Wellencharakters" von Teilchenstrahlung (zunächst Elektronenstrahlung) durch Davisson und Germer (1927). Die Argumentation folgte Abschnitt 4, nachdem die deBroglie-Wellenlänge λ = h/p ins Spiel gebracht war. Schon vorher war Bragg-Streuung von Röntgenstrahlen an ähnlichen Kristallgittern bekannt, also der Streuung von Röntgenphotonen. In beiden Fällen lag der Fokus auf Beugung und Interferenz von Wellen, bei Elektronenstrahlung von Wellen zunächst noch unbekannter Art, deBroglie-Wellen genannt.
Andererseits wissen wir mittlerweile, dass Photonen, Elektronen, Neutronen und andere atomare Teilchen wirklich Quantenteilchen im Sinne der Quantenphysik (aber keine klassischen Teilchen) sind, die alle einen Impuls p haben. Wie sieht jetzt also Bragg-Streuung im Licht einer Teilchentheorie aus?
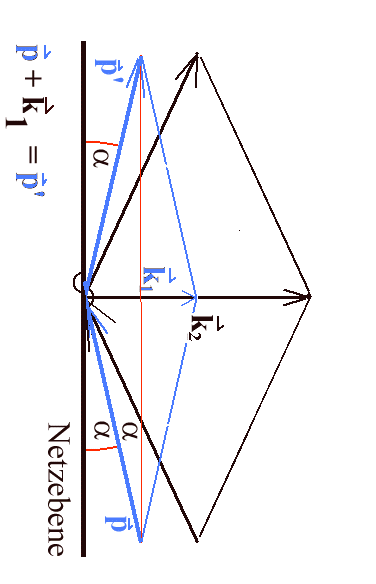
Abb. 8: Impulse bei der Bragg-Reflexion |
Photonen (wie auch die Mikrowellen-Photonen,
Röntgen-Photonen) werden als Teilchen bei der Wechselwirkung mit
dem Kristall wie bei Stößen abgelenkt. Die Impulse p und
p' des einfallenden bzw. austretenden Teilchens (Abb. 8)
sind gleichgerichtet wie die entsprechenden ein- und austretenden
Strahlen. Der Winkel α tritt auch hier auf.
Wegen des Impulserhaltungssatzes muss also ein Impulsvektor, z.B. k1, des Kristalls beteiligt sein. Aus der Zeichnung ergibt sich: p + k1 = p' . Offenbar können nur Impulse k1, k2, ... vom Kristallgitter übertragen werden, die ein ganzzahliges Vielfaches eines grundlegenden Gitterimpulses k1 sind (das n-fache; n = 1, 2, 3, ...). Dieser steht senkrecht auf der Netzebene. Das entspricht dem Versuchsergebnis.
k sei der Betrag des kleinsten Gitterimpulses k1. Es gilt dann nach Abb. 8 wegen p = h/λ: sin(α) = (k·n/2)/p = k·n/(2·p) = k·n·λ/(2·h) bzw. λ·n = sin(α)·2·h/k (n = 1,2,3, ...) Sie haben damit auch hier einen Zusammenhang zwischen dem Winkel α und der Wellenlänge λ. Es fehlt noch k. Wir führen vorerst eine Abkürzung d ein: d = h/k bzw. k = h/d , und erhalten im Teilchenbild:
Die Größe d = h/k werden wir später identifizieren. Um die Vielfachen des an das Kristallgitter oder vom Kristallgitter übertragenen Impulses zu verstehen müssten Sie jetzt noch etwas mehr über Festkörperphysik wissen. Sie hängen mit der Periodizität des Kristallgitters zusammen, also der Tatsache, dass sich nach einer Gitterkonstanten d "alles wiederholt". Festkörperphysiker sprechen in diesem Zusammenhang vom "reziproken Gittervektor". Hier kommt also die Wellentheorie des Kristalls bzw. die Quantentheorie herein. Abgesehen davon haben wir die Kristallgitterbeugung jetzt korpuskular gedeutet. Bei dieser Überlegung bleibt Einiges offen: 1. Warum gibt es nur solche Zusatzimpulse? Warum wirkt sich die Periodizität des Kristallgitters gerade so aus? 2. Warum erhalten Teilchen unter anderen Einfallswinkeln α keine solchen Zusatzimpulse und werden in nennenswertem Maße abgelenkt? 3. Mit welcher Wahrscheinlichkeit wird ein so eintretendes Teilchen abgelenkt? Die Frage hängt mit der 2. Frage zusammen. Auf diese Fragen kann nur die komplette Quantentheorie der einfallenden Teilchen und des Kristalls eine Antwort geben.
|
Die Wellentheorie (Abschnitt 4) hatte die gleiche Bragg-Beziehung geliefert und wir können danach d als den Netzebenenabstand identifizieren und kn = k · n als h/d · n (n = 1, 2, ... ). Das sind die Beträge der Gitterimpulse. Der Betrag des Kristallgitterimpulses hängt vom Kehrwert des Netzebenenabstands d ab. Bis auf den Faktor h nennt man sie die Vektoren des reziproken Gitters. Damit ist Bragg-Streuung korpuskular gedeutet.
Die Situation entspricht der Situation der Beugung und Interferenz an einem Beugungsgitter. Auch diese konnte in einer gewissen Weise korpuskular gedeutet werden, wenn die Periodizität des Gitters quer zum einfallenden Strahl berücksichtigt wurde. Auch dort wurde zum vollständigen Verständnis die Quantentheorie benötigt und nicht allein ein Wellen- oder ein Teilchenbild.
Auch bei einer Wellentheorie der Bragg-Streuung entsprechend Abschnitt 4 bleibt Einiges offen:
1. Hier scheint nur ein einziges Faktum vom Kristall wichtig zu sein: Die Periodizität der Streuzentren und der Netzebenenabstand. Geht sonst der Kristall gar nicht ein?
2. Nimmt man wirklich eine kontinuierlich verteilte Interferenzfigur wahr mit einer sich stetig verändernden Intensitätsverteilung? Das Experiment zeigt doch, dass bei kleiner Leistung der Quelle der Nachweis einzelner zufällig verteilter Teilchen auffällt!
3. Wie groß ist die Intensität der in eine bestimmte Richtung α gestreuten Welle? Was hat sie mit der Statistik der Teilchennachweise zu tun? Deren Streuung weist darauf hin, dass hier zufällige Vorgänge stattfinden.
Wieder: Auf diese Fragen kann nur die komplette Quantentheorie der einfallenden Teilchen und des Kristalls eine Antwort geben.
Immerhin ist jetzt plausibel: Wenn Röntgenphotonen gemäß der Darstellung oben beim Stoß mit dem Kristall einen Kristallimpuls (Phononenimpuls) aufnehmen, dann sollten auch andere Teilchen, wie Elektronen, Neutronen oder Atome, einen entsprechenden Impuls aufnehmen und Bragg-gestreut werden können. Dies legt eine Beugung von Elektronen, Neutronen oder Atomen an Kristallgittern nahe, ohne dass explizit auf eine Beschreibung durch Wellen Bezug genommen wird.
6. Folgerung:
Gewisse charakteristische Aspekte der Bragg-Reflexion an Kristallen sind sowohl korpuskular wie wellentheoretisch zu erklären. Zu einer vollständigen Erklärung braucht man die ganze Quantentheorie. Ähnlich war das schon bei der Gitterbeugung und beim Fotoeffekt. Dies wirft einigen Zweifel darauf, ob durch eines dieser Experimente ein "Wellencharakter" oder "Teilchencharakter" wirklich bewiesen wird, bzw. ob behauptet werden darf, dass sich bestimmte Erscheinungen wirklich "nur" durch ein "Wellenmodell" oder ein "Teilchenmodell" erklärt werden können, bzw. dass man so auf einen "Teilchen-" oder "Wellencharakter" schließen muss. "Quanten sind anders" (Göritz)! Immerhin brachten die beschriebenen Experimente die Physiker auf den richtigen Weg zur Erkenntnis!
7. Anhang
 |
 |
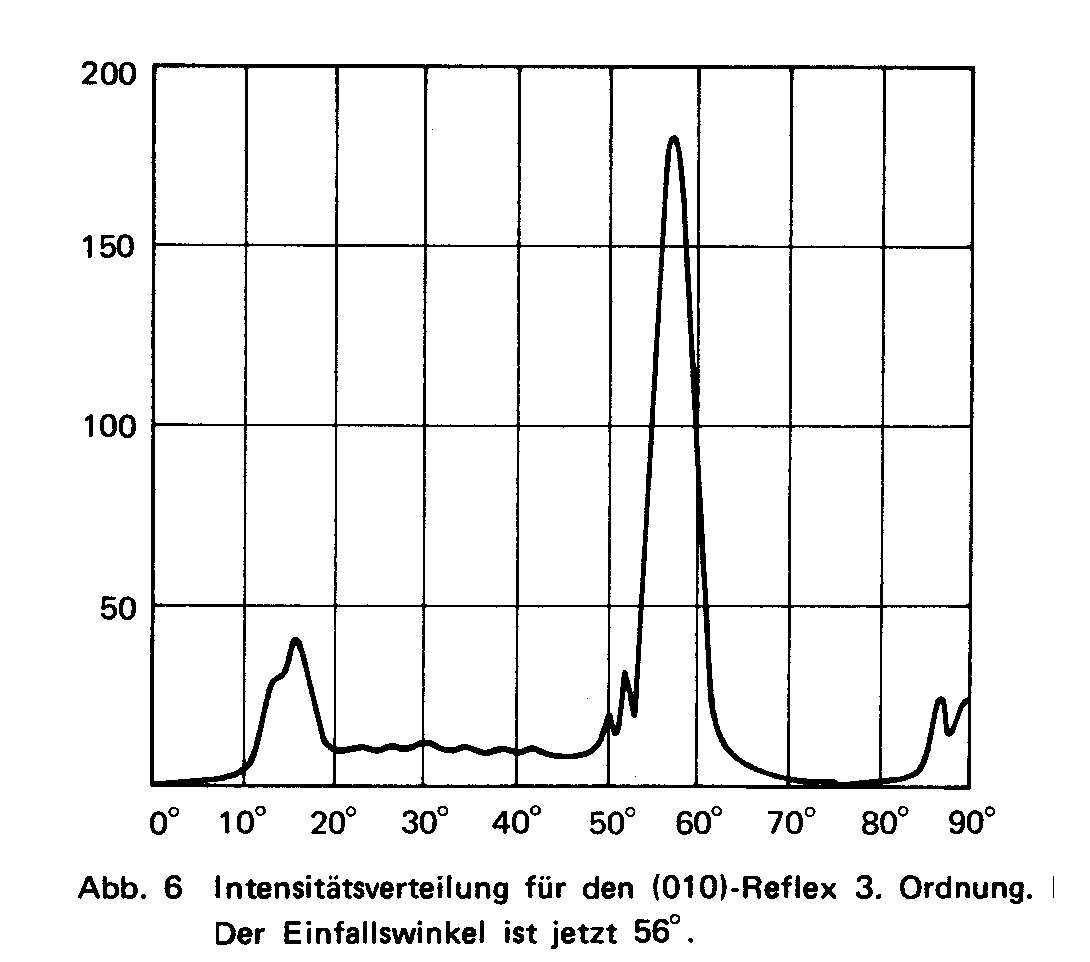 |
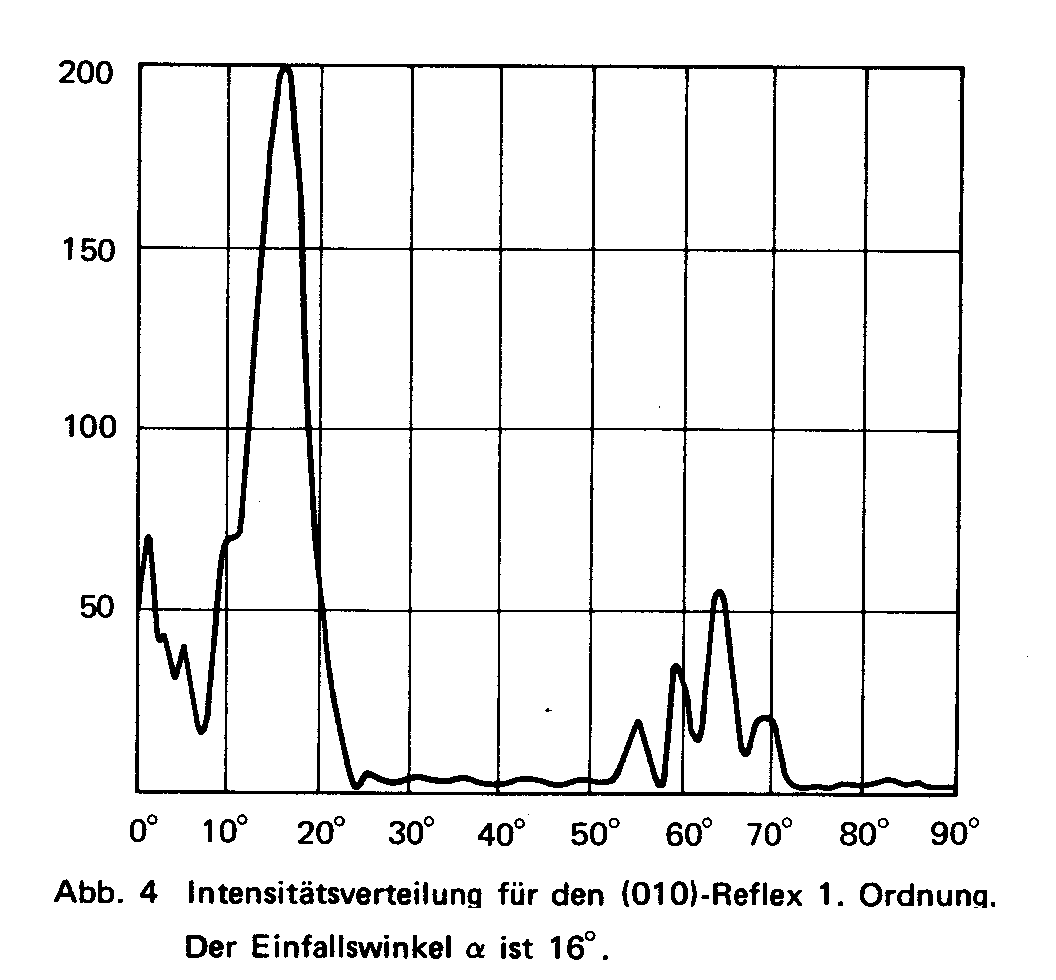
| Aus der Originalarbeit (1): gemessene US-Spektren für die drei Reflexe. Dabmals gab es noch nicht die Vorrichtung für die Drehkristallmethode. Deswegen wurde dabei mit feststehendem Sender gemessen. Die Schärfe der Reflexe beeindruckt. | ||
8. Literatur:
(1) Hübel, Horst; Hübel, Otto: Bragg-Streuung an einem Modellkristall mit Ultraschallwellen, Physik und Didaktik, 9 (1981) 2, S. 167-173
(2) Hübel Horst, Poor Man's Bragg Reflection, Tagungsbeitrag 1988: International Conference on Teaching Modern Physics Condensed Matter 12-16 Sept 1988, in: International Conference Teaching Modern Physics - Condensed Matter - Proceedings, World Scientific, Singapore, 1989
( März 2016 : Zeichensatz geändert )