PHYSIK-LERNEN MIT DEM COMPUTER THEMA: Alles über die gleichmäßig beschleunigte Bewegung: Galileis Darmsaitenmethode im Schülerversuch PROGRAMM: GALILEI Horst Hübel

Schülerversuch: Durch Handstoppen mit dem PC-Programm GALILEI ermitteltes t-x-Diagramm einer gleichmäßig beschleunigten Bewegung auf der Galileischen Kugelrinne. (Die folgenden Bilder sind entweder von unterschiedlichen Programm-Versionen oder mit unterschiedlichen Graphik-Varianten erzeugt.)

---

ZIEL:                                                                                                                          zurück

Ein Zeit-Ort-Diagramm oder auch ein Zeit-Geschwindigkeit-Diagramm der beschleunigten Rollbewegung längs einer schiefen Ebene soll registriert werden. Mittels Maus-Tastendruck wird die jeweilige Zeit beim Passieren einer Marke vom Computer gestoppt und registriert.

---

BESCHREIBUNG:                                                                                                                          zurück

Nachdem die mittelalterlichen Wissenschaftler die Notwendigkeit erarbeitet hatten, die Natur mittels Messungen zu erfassen, war Galileo Galilei (1564 - 1642) der erste, dem dies bei einer beschleunigten Bewegung wirklich gelang. Es ging bei ihm um die Gesetze des Freien Falls. In Ermangelung geeigneter Kurzzeituhren wandte er dazu zwei Tricks an: erstens verlangsamte er die Bewegung, indem er eine Kugel eine nur schwach geneigte schiefe Ebene hinabrollen ließ, zweitens markierte er Wegabschnitte, für die jeweils die gleiche Zeit benötigt wird. Galilei spannte zu diesem Zweck Darmsaiten quer über die Fallrinne. Wenn nun die herabrollende Kugel über sie hinwegsprang, gab es einen kurzen Ton. Galilei verschob die Darmsaiten solange, bis gleichmäßige Zeitabstände zwischen den Marken bestanden. Er kontrollierte das angeblich, indem er eine Melodie summte. Menschen mit gutem Rhythmusgefühl können so Zeitabschnitte sehr genau einhalten.

Der Versuch soll hier, etwas abgewandelt, wiederholt werden: Verwenden Sie als schiefe Ebene eine Vorhangschiene oder eine U-förmige Alurinne aus einem Bastelgeschäft oder Baumarkt. Lassen Sie eine Kugellagerkugel hinabrollen oder eine Murmel. Markieren Sie mit einem Filzstift beliebige Marken und stoppen Sie die Zeiten von Marke zu Marke mit dem vorliegenden Computer-Programm, nachdem Sie dem Programm die Position der Marken mitgeteilt haben.

Schülerversuch: Untersuchung der Bewegungsgesetze an der schiefen Ebene (Galilei-Rinne) durch Handstoppen. Der PC dient als Vielfachuhr und zum Darstellen der Graphiken	Schülerversuch: Aufnahme des t-v-Diagramms einer gleichmäßig beschleunigten Bewegung einer auf der Galilei-Rinne rollenden Kugel durch Handstoppen

In einer Versuchsvariante kann auch für beliebige Marken, z.B. äquidistante, das x(t)-Diagramm aufgenommen werden. Das Stoppsignal kann außer von der Tastatur auch von einem äußeren Signalgeber, z.B. von Lichtschranken kommen (nicht in jeder Programm-Variante implementiert).

---

FRAGESTELLUNGEN:                                                                                                                          zurück

- Wie erfolgt eine beschleunigte Bewegung?

- Zeit-Ort-Gesetz x(t) einer gleichmäßig beschleunigten Bewegung?

- Zeit-Geschwindigkeit-Gesetz v(t)?

- Definition der Beschleunigung als Steigung im v(t)-Diagramm?

- Einfluß der Bahnneigung?

- Proportionalität zwischen Hangabtriebskraft und Beschleunigung?

- Einfluß des Trägheitsmoments der rollenden Kugel auf die Beschleunigung? (Vergleich mit einer gerechneten Gleitbewegung)?

- Auswertungsverfahren für gleichmäßig beschleunigte Bewegungen: v(t)-Diagramm, x(t)-Diagramm, √x (t) - Diagramm?

- 2. Gesetz von Newton (F prop. a bei konstanter Masse)

---

EINSATZMÖGLICHKEITEN:                                                                                                                 zurück

Schülerversuche im Klassenverband mit mehreren Gruppen; häuslicher Schülerversuch am schülereigenen Computer; Demonstrationsversuch an Schulen mit geringer Ausstattung

---

HINWEISE ZUM EINSATZ:                                                                                                                  zurück

Mit Stativmaterial oder mit untergelegten Diagläsern, Disketten etc. könnte eine bestimmte Steigung der schiefen Ebene vorgegeben werden. Bei der dann bekannten Hangabtriebskraft könnte die Beschleunigung bzw. das x(t)-Diagramm bei einer Gleitbewegung (ohne Reibung) berechnet werden. Auf die unterschiedliche Beschleunigung bei der Rollbewegung und bei der Gleitbewegung der Kugel könnte im Zusammenhang mit dem Trägheitsmoment hingewiesen werden.

---

TECHNISCHE HINWEISE:                                                                                                                    zurück

Wegen der Einfachheit des Versuchs wurde dieses Programm für das Stoppen durch Tastendruck entwickelt.

---

TYPISCHE VERSUCHSERGEBNISSE:                                                                                                zurück

Wurzel aus dem Ort x in Abhängigkeit von der Zeit: Die Linearität der ungefähr erreichten Ursprungsgerade bestätigt die quadratische Gesetzmäßigkeit für den Ort x

 

Ort x in Abhängigkeit von der Zeitdifferenz zwischen 2 Messungen: Die Marken sind - entsprechend Galileis Methode - so günstig gewählt, dass im Rahmen der Messgenauigkeit gleiche Zeitdifferenzen zwischen dem Passieren aufeinanderfolgender Marken vorliegen.

  

Großanzeige von Zeit t und Ort x, z.B., wenn das Programm in einem Demonstrationsversuch eingesetzt werden soll

  

Wurzel aus dem Ort x in Abhängigkeit von der Zeit t für verschiedene Bahnneigungen

Geschwindigkeit v in Abhängigkeit von der Zeit, gemessen nach der Zeitmittenmethode: Beachtliche Linearität trotz der primitiven Meßmethode!

Geschwindigkeit v in Abhängigkeit von der Zeit t bei verschiedenen Bahnneigungen: daraus ergibt sich die Beschleunigung a (Steigung) prop. zur jeweiligen Hangabtriebskraft (durch untergelegte Diagläser (2,4,6,8) wurde die Hangabtriebskraft in gleichen Schritten erhöht)

 

---

DIDAKTISCHE HINWEISE:                                                                                                                    zurück

Messung der Beschleunigung:

Unabhängig davon, ob der Steigungsbegriff zur Verfügung steht, wird die Beschleunigung gemessen als Steigung (Differenzenquotient Δv/Δt) des t-v-Diagramms mittels eines Steigungsdreiecks. Das Programm kann zwar Ausgleichskurven berechnen und zeichnen, aus denen ebenfalls die Beschleunigung zu erschließen wäre. Das ist aber nicht so gedacht. Vielmehr sollten die Schüler durch explizite Nutzung des Steigungsdreiecks im t-v-Diagramm die Definition der Beschleunigung einüben. Die Anzeige des mitlaufenden Steigungsdreiecks wird mit der linken oder mit beiden Maustasten abgeschlossen. Im zweiten Fall werden Δv und Δt mit Großziffern angezeigt.

Geschwindigkeit v in Abhängigkeit von der Zeit, gemessen nach der Zeitmittenmethode:   Aus dem mit der Maus mitlaufenden Steigungsdreieck folgt direkt die Beschleunigung. Glatte Werte von Δt, wie hier 3,000 s, erleichtern das Berechnen der Beschleunigung

Zur Zeitmittenmethode:

Die Zeitmittenmethode erlaubt es, Momentangeschwindigkeiten bei gleichmäßig beschleunigten Bewegungen exakt für beliebige endlichen Zeitintervalle aus einer Messung zu ermitteln.

Die Durchschnittsgeschwindigkeit v = dx/dt in einem Intervall dt stimmt i.A. nicht mit der Momentangeschwindigkeit an den Intervallrändern überein. Dies wird häufig benutzt, um eine Verbindung zwischen dem Begriff der Momentangeschwindigkeit und der Definition der Ableitung durch den Grenzübergang verschwindenden Zeitintervalls zu diskutieren.

Physikalisch natürlicher ist es, die Durchschnittsgeschwindigkeit im Intervall nicht einem Intervallrand zuzuordnen, sondern der Intervallmitte ('Zeitmitte'). Wenn sich in einem Zeitintervall dt die Momentangeschwindigkeit ändert, ist die Annahme plausibel, daß die Durchschnittsgeschwindigkeit der Momentangeschwindigkeit in der Mitte des Zeitintervalls am nächsten kommt. Bei Bewegungen mit a = konst. stimmt die Durchschnittsgeschwindigkeit, wie man leicht nachrechnen kann, mit der Momentangeschwindigkeit in der Zeitmitte sogar exakt überein:

t	.	v1 = v0	x1 = x0	.
t+dt	.	v2 = v0 + a·dt	x2 = x1 + v0·dt + ½·a·dt2	vD=(x2 - x1)/dt  = v0 + ½·a·dt
t + ½·dt	.	v = v0 + a·½·dt = vD	.	.

Statt - im Interesse der Infinitesimalrechnung - physikalisch gewaltsam die Durchschnittsgeschwindigkeit dem Intervallrand zuzuordnen, kann es sich empfehlen, die physikalisch naheliegendere Zuordnung vorzunehmen, zumal da diese bei den schulischen Bewegungen meist sogar exakt ist.

Im Programm wird demnach die Durchschnittsgeschwindigkeit in beliebigen Zeitintervallen der Zeit der jeweiligen Intervallmitte zugeordnet. Deshalb werden Ortsmessung und v-Messung im Programm getrennt, da Ort x und Geschwindigkeit v zu verschiedenen Zeiten gelten (am Intervallanfang bzw. zur Intervallmitte).

Zum Nachweis des 2. Gesetzes von Newton:                                                                                          zurück

Bei der Bahnlänge l und der Überhöhung h gilt für die Hangabtriebskraft F_H = m.g. h/l. Die beschleunigende Kraft ist also proportional zur Höhe h. Die gesuchte Proportionalität zwischen a und F_H ist also gleichbedeutend mit der Proportionalität a prop. h. Diese gilt auch nach der korrekten Theorie, wenn das Drehmoment und das Trägheitsmoment der rollenden Kugel berücksichtigt werden. Es muß sorgfältig durch eine kleine anfängliche Bahnneigung für Reibungsausgleich gesorgt werden. Zunächst wird man sicher verschweigen, dass hier der Translation eine Rotation überlagert ist, so dass die Beschleunigung vom Trägheitsmoment (prop. m) abhängt.

---

     

MENUEPUNKTE:	zurück
I DESK	I.1 QUIT Bricht das Programm ab. I.2 START Beginnt eine neue Messung. Das Programm verbleibt zunächst in einem Wartemodus. Dabei ertönt ein Pfeifton, wenn die Startbedingungen günstig sind (z.B. wenn die Lichtschranke, die das Startsignal geben soll, noch nicht unterbrochen ist, oder wenn das Programm auf den startenden Tastendruck wartet. Erst nach erneuter Betätigung einer Taste oder einer Maustaste startet die Uhr bzw. ist bereit zum Start durch ein externes Signal. I.3 INFO Informiert über das Programm, erläutert einige der Fragestellungen, die mit Hilfe des Programms bearbeitet werden können. I.4 AUTOR Nennt den Autor des Programms. I.5 LIZENZ Nicht implementiert
II MESSART	II.1 HANDSTOPP EIN/AUS Schaltet um zwischen Stoppen durch Tastendruck oder durch externes Signal (letzteres hier nicht implementiert). Funktion ist also nicht verwendbar. II.2 ÄQUIDISTANZ Meldet dem Computer äquidistante Marken. Der Computer fragt dann nach der Zahl der Messungen und den Abstand der äquidistanten Marken. II.3 x-EINGABE Meldet dem Computer, dass willkürliche Ortsmarken benutzt werden sollen. Das Programm fragt dann nach der Zahl der Marken und deren Positionen. II.4 1 SIGN.: ssss Nicht implementiert II.5 2 SIGN.: ffff Nicht implementiert II.6 3 SIGN.: sfsf Nicht implementiert II.7 4 SIGN.: fsfs Nicht implementiert
III MODUS	III.1 ORTSMESSUNG Registriert Ort x und Zeit t. Lässt nur Ausgabe von x und Wurzel(x) in Abhängigkeit von t zu. III.2 v-MESSUNG Registriert Geschwindigkeit v und Zeit t. lässt nur Ausgabe von v in Abhängigkeit von t zu. v wird nach der Zeitmittenmethode ermittelt, die bei konstanter Beschleunigung exakt ist. III.3 INTERFACE-TEST Nicht implementiert
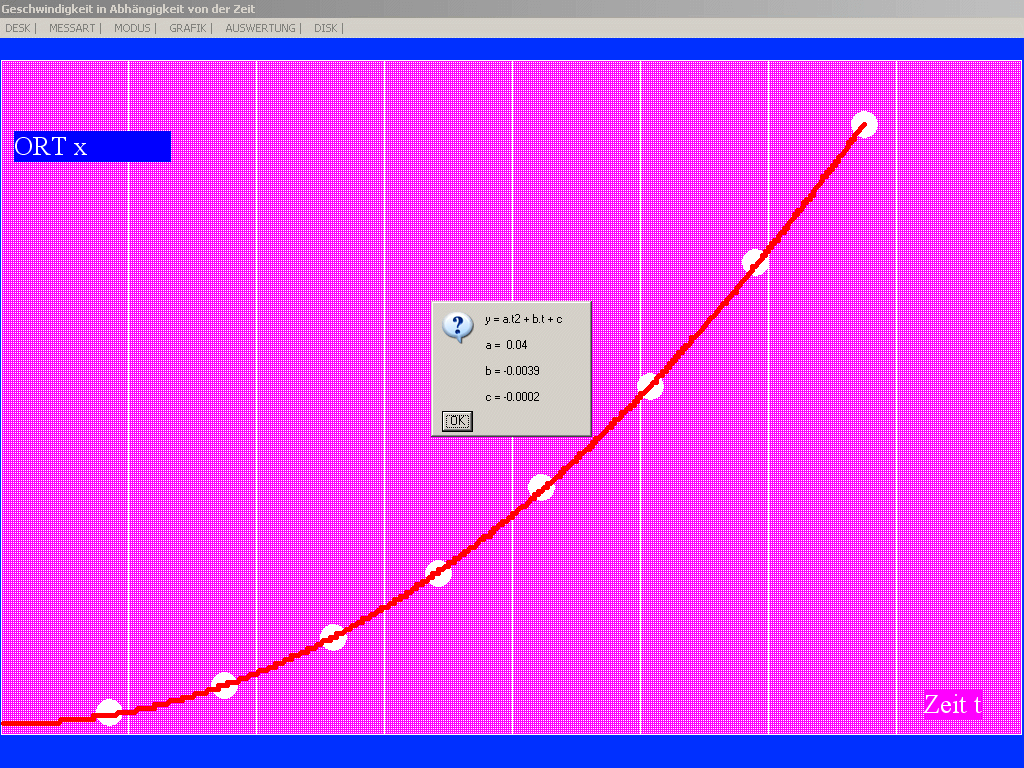
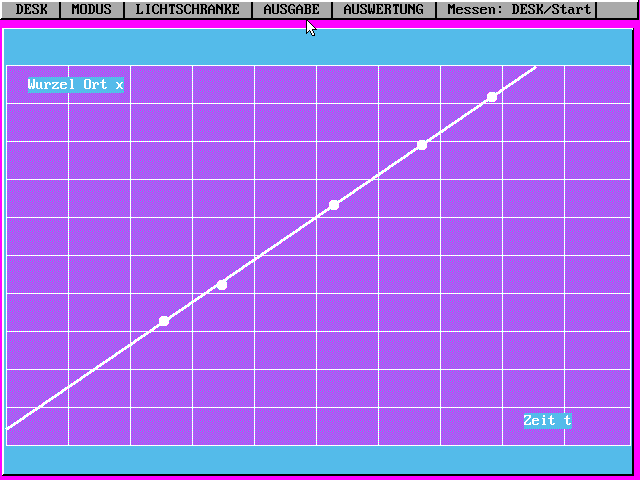
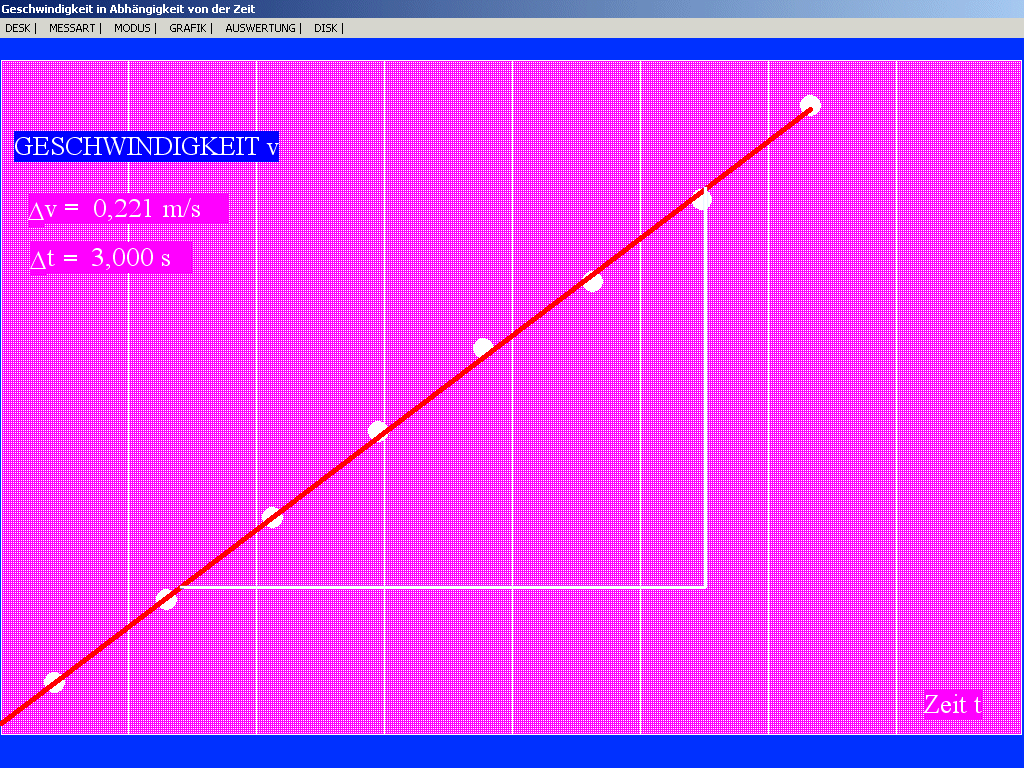
IV GRAFIK	IV.1 WAHL: x(t) Falls Ortsmessung gewählt: Erlaubt Ausgabe von x(t). IV.2 WAHL: SQR(x(t)) Falls Ortsmessung gewählt: Erlaubt Ausgabe von SQR(x(t)). Zwischen beiden Einstellungen kann frei umgeschaltet werden. Die Auftragung von SQR(x)  ist insbesondere dann sinnvoll, wenn die quadratische Gesetzmäßigkeit von x(t) bestätigt werden soll (Gerade für t-SQR(x)-Diagramm). IV.3 WAHL: v(t) Falls Geschwindigkeitsmessung gewählt: Erlaubt allein Ausgabe von v(t). Wird automatisch eingestellt, wenn v-Messung gewählt wird. IV.4 ZEIGEN Bringt den gewählten Graphen auf den Bildschirm; überschreibt frühere Meßkurven. IV.5 LÖSCHEN Löscht den Bildschirm, nicht aber die Messdaten. Diese können erneut in einem sonst leeren Koordinatensystem gezeigt werden. IV.6 ZEITDIFFERENZ EIN/AUS Schaltet um zwischen Messung der Gesamtzeit seit Start (Voreinstellung) und Messung von Zeitdifferenzen zwischen zwei aufeinander folgenden Messungen. Insbesondere für den originalen Galilei-Versuch ist diese Meßart zweckmäßig. IV.6 y-FAKTOR Ermöglicht Maßstabsveränderungen, so dass der Bildschirm optimal genutzt wird. IV.7 t-FAKTOR Ermöglicht Maßstabsveränderungen, so dass der Bildschirm optimal genutzt wird.
V AUSWERTUNG	V.1 GROßZIFFERN Gibt eine Liste von Messdaten in Großzifferndarstellung aus. Wartet nach jeder Ausgabe auf einen Tastendruck. V.2 LISTE Bringt eine Liste der Messdaten je nach Wahl der Messart auf den Bildschirm. V.3 DRUCKEN Gibt eine Liste der Messdaten je nach Wahl der Messart auf dem Drucker aus. V.4 AUSGLEICHSKURVE Zeichnet zusätzlich in den Graphen eine Ausgleichskurve (Parabel oder Gerade). V.5 STEIGUNGSDREIECK Mit der Maus lassen sich ein linker und ein rechter Begrenzungspunkt des Steigungsdreiecks setzen. Gleichzeitig werden die Differenzen Δv und Δt angezeigt. Daraus lässt sich leicht die Beschleunigung berechnen, besonders dann, wenn für Δt glatte Werte gewählt werden. Wenn beide Maustasten gleichzeitig gedrückt werden, lassen sich im Demonstrationsversuch Δv und Δt bildschirmfüllend anzeigen. V.6 HARDCOPY Nicht implementiert V.7 BESCHLEUNIGUNG Ermittelt aus den Daten der Ausgleichskurve die Beschleunigung. Aus didaktischen Gründen ist diese Funktion nicht in allen Fällen sinnvoll einzusetzen.
VI DISK	VI.1 LADEN Lädt eine Datei von Messdaten aus einem frei wählbarem Verzeichnis. VI.2 SPEICHERN Speichert eine Datei von Messdaten in ein frei wählbares Verzeichnis.

---

LITERATURHINWEIS:                                                                                                                          zurück

Stillman Drake, Galilei, Herder 1999, S. 60

.

Download des Programms GALILEI (ca. 500 kB; ZIP-Datei)