Was hat der ARDUINO mit der Selbstinduktion zu tun?
Das Gesetz
der Selbstinduktion (Uind = - L·ΔI/Δt in einfachen Fällen
- Uind prop. zur "Änderungsgeschwindigkeit der
Stromstärke") soll im Experiment nachgewiesen werden. Statt
"Änderungsgeschwindigkeit der Stromstärke" ΔI/Δt kann man auch sagen:
Steigung der t-I-Funktion. Der Mikroprozessorbaustein ARDUINO wird dabei
eingesetzt, um - z.B. im Schülerversuch - die Stromstärke und den
resultierenden Spannungsverlauf zu registrieren und das Gesetz der
Selbstinduktion dem Experiment zu entnehmen, bzw. die Induktivität
sinnvoll zu definieren. Die Messwerte werden dabei aus dem Arduino eigenen
"Seriellen Monitor" kopiert und - nach Vereinbarung eines Kommas als
Trennzeichen zwischen den einzelnen Messwerten - in ein
Tabellenkalkulationsprogramm (TBK) übertragen, wo Graphen angelegt werden.
Der besondere Vorteil des Vorgehens besteht darin, dass die Messwerte im
TBK weiter verarbeitet werden können. So kann dort die Steigung der
t-I-Funktion ermittelt und ebenfalls graphisch dargestellt werden. Ein
dI/dt-Uind-Graph demonstriert eindringlich die
Proportionalität; die Proportionalitätskonstante wird als Induktivität L
definiert.
Ziel der Untersuchung von Ein- und
Ausschaltvorgängen im Schülerversuch
Möglichst im Schülerversuch sollen Ein- und Ausschaltvorgänge an einer
Spule im Gleichstromkreis untersucht werden. Über einen Taster wird der
Spule Energie aus einer Batterie zugeführt. Eine geeignete Schaltung dafür
ist die "Grundschaltung"
(auch Abb. 1) mit den Widerständen R1 und R2. Der
ARDUINO stellt eine preiswerte Möglichkeit bereit, den Spulenstrom (und
evtl. auch die Induktionsspannung zu messen). Es wird z.B. eine billige Schülerversuchsspule
verwendet mit relativ hoher Induktivität (ab L = 0,1 H) und sehr kleinem
Innenwiderstand (ab R = 1,5 Ω). Sie hat auf dem gleichen Ferritkern zwei
identische Wicklungen. Wegen der im Stromkreis eingebauten Widerstände R1
und R2 haben I und Uind i.A. exponentielle Zeitabhängigkeiten,
die üblicherweise theoretisch nicht ganz einfach, aber auf interessante
Weise erfasst werden.
Von der Theorie
sind für die Schule besonders vier Grundprinzipien
wichtig: das Gesetz der Spule (Selbstinduktionsgesetz), die
Spannungsbilanz, die Tatsache, dass die Stromstärke sich stetig verhält,
also "keine Sprünge macht" und Folgerungen aus dem stationären Strom
(Spitzenwerte).
Für den Ausschaltvorgang erhält man eindeutige Verhältnisse nur, wenn in
der Grundschaltung ein endlicher Widerstand R2 vorhanden ist.
Weil das vielfach übersehen wird, findet man in der Literatur, in
offiziellen Musteraufgaben und in so genannten "Erklärvideos" oft falsche
Behauptungen, die belegen, dass die Autoren den Sachverhalt nicht
verstanden haben.
Die Stromstärke bei Ein-/Ausschaltvorgängen könnte man auch besonders
einfach mit einem Oszilloskop oder Speicheroszilloskop im
Demonstrationsversuch untersuchen. Im Unterschied dazu hat man bei
Verwendung des ARDUINO die Möglichkeit, die Charakteristika sogar im
Schülerversuch zu gewinnen und die digital erhaltenen Daten weiter zu
verarbeiten, um z.B. Gesetzmäßigkeiten abzulesen, wie Steigungen oder das
exponentielle Verhalten.
Im Konzept des "forschenden Unterrichts" haben
Schülerversuche neben der Plenumsarbeit eine wichtige Funktion.
Der Versuch ist eine Modifikation der Versuche zu Ein-/Ausschaltvorgängen.
Er ist einfacher als der in Arduino und
Selbstinduktion I beschriebene, hat aber auch seine Tücken.
Der Umgang mit dem ARDUINO ist relativ leicht zu lernen; das habe ich anderswo
beschrieben.
Die Mess-Schaltung für den Schülerversuch
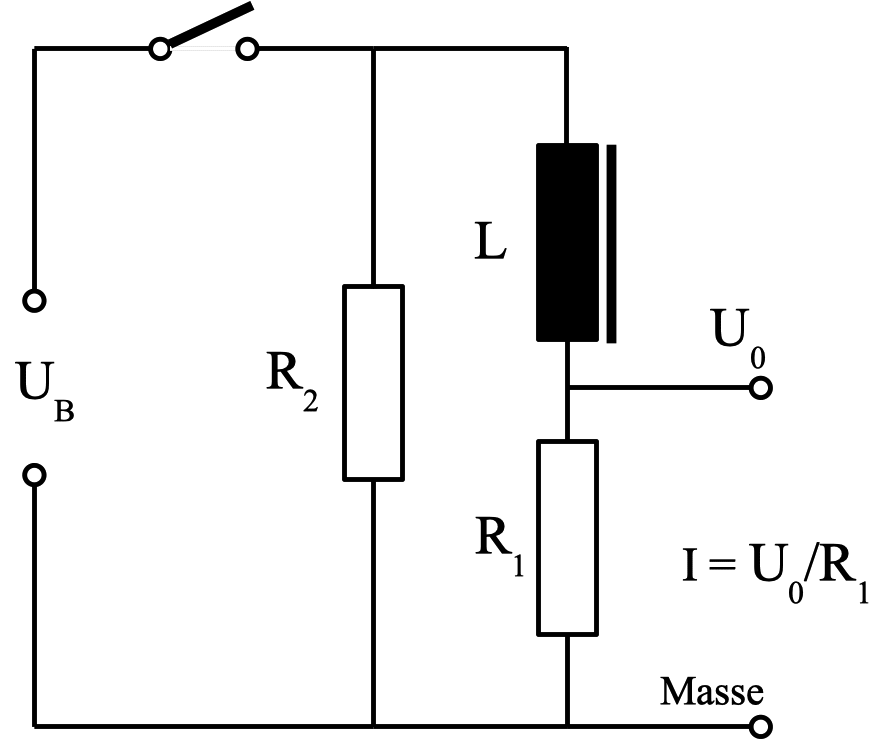 |
Abb. 1: "Grundschaltung",
im SV mit den Daten: L = 0,1 H, R1 = R2 = 100
Ω, UB = 1,5 V - 5 V.
Für die Schülerversuchsspule mit
L = 0,1 H (Ri = 1,5 Ω; oft vernachlässigbar) und mit R1
= R = 100 Ω erhalten Sie in guter Näherung T = L/R1 = 1
ms (für den Einschaltvorgang)
bzw. T' = L/(R1+ R2) = 0,5 ms (für den
Ausschaltvorgang). Das Messinterface muss also schnelle Messungen
zulassen, ca. alle 0,11 ms beim verwendeten Programm für
den Arduino.
|
Gemessen werden soll die Stromstärke I durch die (nichtnegative) Spannung
U0 (I = U0/R1; in Abb. 4: blau). Als
nichtnegative Spannung kann U0 direkt (ohne Pegelwandler) an
einen der Messeingänge des ARDUINO-Prozessors gelegt werden (gegen Masse =
Ground), wenn die Grenzwerte des Prozessors eingehalten werden. Ich
verwende den Analogeingang A0: U0 an PIN19, Masse an PIN04.
Um dagegen die Induktionsspannung (in Abb. 3: rot) mit ihren zwei
Vorzeichen mit dem Arduino direkt zu messen, braucht man auf
einen Pegelwandler,
der die Spannungswerte in den positiven Bereich verschiebt, indem eine
konstante Gleichspannung hinzu addiert wird.
Hier bewährt sich die zweite Wicklung. Denn wenn Selbstinduktion der
Grund für das interessante Verhalten der Stromstärke ist, die auf einer
Änderung des magnetischen Flusses in der Spule ist, muss an der
Sekundärspule eine Induktionsspannung von gleichem Betrag wie an der
Primärspule entstehen, weil beide Wicklungen vom gleichen Fluss durchsetzt
sind. Im Versuch soll der Zusammenhang zwischen der Stromstärke in der
Spule und der Selbstinduktionsspannung ermittelt werden, die beide ja
zeitabhängig sind.
Wenn man etwas mehr über die wirksamen Gesetzmäßigkeiten weiß, kann man Uind
auch mit der Spannungsbilanz
berechnen. Nur wenn Ri wirklich vernachlässigt werden
kann, gilt: UB + Uind = U0, also Uind
= U0 - UB für den Einschaltvorgang bzw. Uind
= U0 (R1 + R2)/R1für den
Ausschaltvorgang. Andernfalls setzt man den Spannungsabfall an Ri
mit Uind = U0 (R1 + Ri)/R1-
UB für den Einschaltvorgang bzw. Uind = U0
(R1+R2+Ri)/R1 für den
Ausschaltvorgang in Rechnung. Die Kalkulationen können (später) im
Tabellenkalkulationsprogramm vorgenommen werden, in dem auch die Messwerte
des ARDUINO graphisch aufbereitet werden.
Realisierung auf der Leybold-Rastersteckplatte, vor
allem für Schülerversuche
|
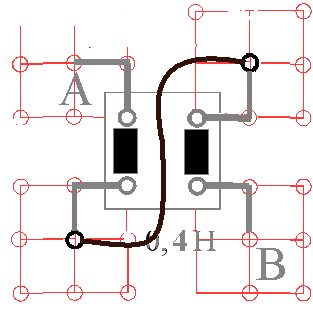 |
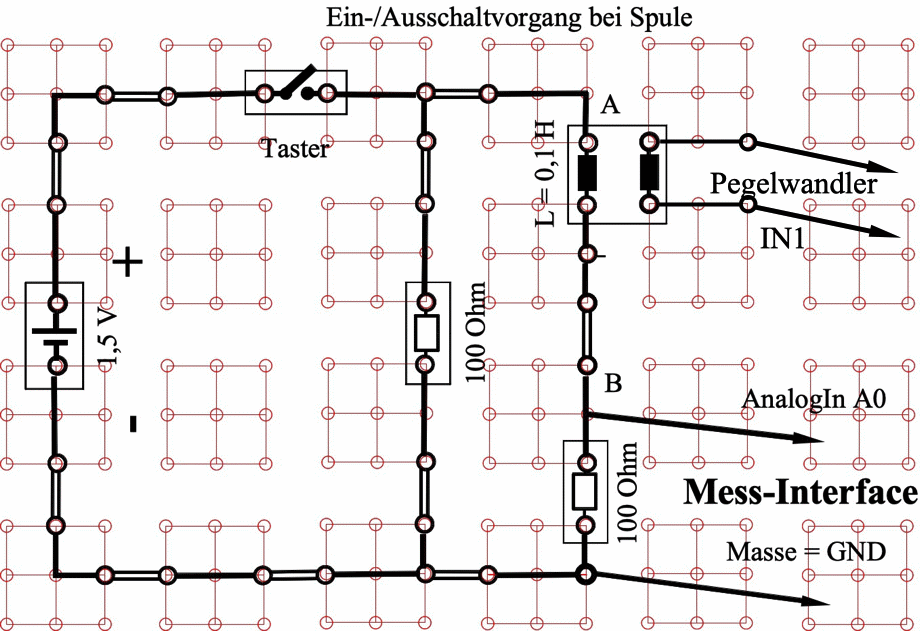
Abb. 2: DINA4-Auflageblatt für das
Leybold-Rastersteckplatte zum sicheren Aufbau der Mess-Schaltung
durch die Schüler im SV. Die Sch stecken die Bauteile durch das
aufgelegte Blatt hindurch. Die rot gezeichneten "Inseln" (in sich
leitend) werden untereinander durch Bauteile oder leitende
Verbindungsstecker ("Doppelstriche") verbunden. Die 2. Wicklung der
Schülerversuchsspule kann bei
geeigneter Beschaltung zu erhöhter
Induktivität führen oder zur direkten Messung der
Induktionsspannung herangezogen werden, wenn die Induktionsspannung
durch einen Pegelwandler in den nichtnegativen Bereich verschoben
wird. Andernfalls droht Zerstörung des ARDUINO.
|
Abb. 2a: Beschaltung für 4-fache Induktivität. Dann steht
allerdings die zweite Wicklung nicht mehr zur Messung der
Induktionsspannung zur Verfügung.
Bei einer Wicklung ergibt sich die Induktivität L = 0,1 H, bei der
Beschaltung oben L = 0,4 H. Mit 2 SV-Spulen in Reihe kann man bis zu
0,8 H erzielen.
|
Mit dem ARDUINO werden hier also Stromstärke und Induktionsspannung
gemessen. Dazu dienen die gleichen Sketches wie für Ein-/Ausschaltvorgänge
an der Spule, allerdings auf 2-kanalige Messung erweitert Ein-/Ausschaltvorgänge
an der Spule II . Die Messwerte werden in den Arduino eigenen
Seriellen Monitor eingelesen, von dem aus auch der Sketch gestartet wird.
Sie werden kopiert und - nach Vereinbarung eines Kommas als Trennzeichen
zwischen zwei Daten - in das Tabellenkalkulationsprogramm übertragen. Im
TBK wird nun die Zeitableitung der Stromstärke ermittelt (vorbereitet in ODS-
oder XLS-Format). Zwei Graphen zeigen
die Ergebnisse: 1. mit Stromstärke und Induktionsspannung in Abhängigkeit
von der Zeit, und 2. die Induktionsspannung in Abhängigkeit von der
Ableitung der Stromstärke.
Wenn Sie der Meinung sind, dass die Sch nicht viel davon haben, wenn das
TBK so schnell den dI/dt-Uind-Graphen zeichnet, können Sie
diesen Graphen ja mit wenigen Werten der Tabelle von den Sch mit der Hand
zeichnen lassen. Dann "springt" die Proportionalität vielleicht eher "ins
Auge". Den Wert der Induktivität sollten die Sch auf jeden Fall mit den
Koordinaten des Ursprungs und eines weiteren Punktes auf dem Graphen
ermitteln.
Im 1. Diagramm werden die exponentiellen Zeitabhängigkeiten dargestellt,
im 2. und 3. Diagramm das Gesetz der Selbstinduktion für den Einschalt-
und den Ausschaltvorgang: Uind prop. dI/dt. Die
Proportionalitätskonstante L wird als Induktivität definiert.
Um aus den gemessenen I-Werten eine "Änderungsgeschwindigkeit der
Stromstärke" (Ableitung dI/dt) möglichst genau zu ermitteln, wird im
TBK-Programm durch 3 Messpunkte eine Parabel gelegt, deren Ableitung als
gemessenes dI/dt interpretiert wird.
Messergebnisse mit dem ARDUINO
|
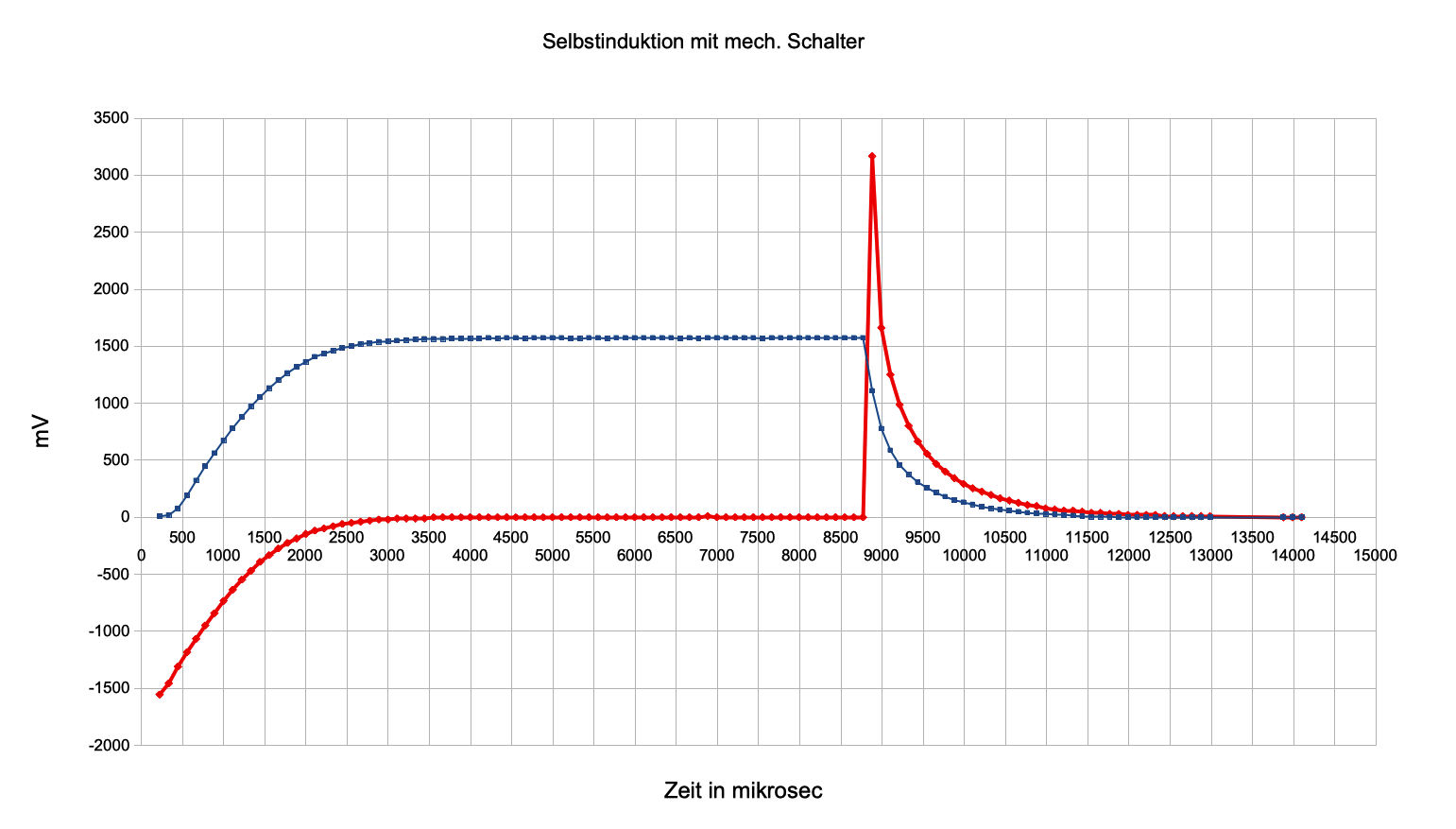
Abb. 3: Zeitverlauf von Stromstärke
(blau) und (Selbst-)Induktionsspannung (rot) beim
Ein-/Ausschaltvorgang, mittels der Schülerversuchsspule gemessen.
Man erkennt die Spitzenwerte: Induktionsspannung beim
Einschalten = negative Batteriespannung, Induktionsspannung beim
Ausschalten = doppelte Batteriespannung, weil R2 doppelt
so groß wie R1.
Beide Spitzenwerte sind vom Arduino errechnet und zu den gemessenen
hinzufügt. |
|
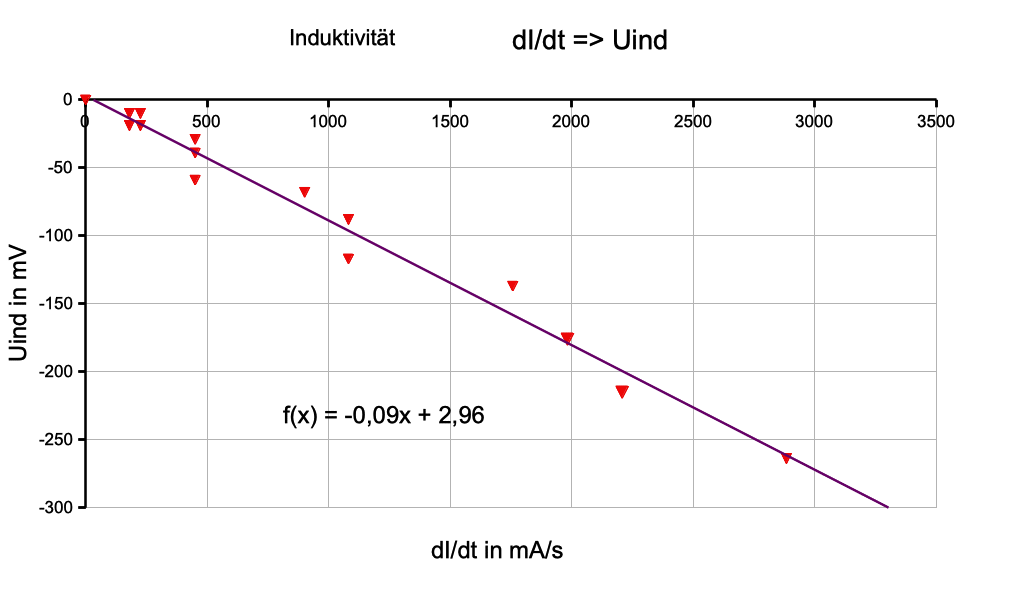
Abb. 4:
(Selbst-)Induktionsspannung in Abhängigkeit von der
"Änderungsgeschwindigkeit der Stromstärke" dI/dt beim
Ausschaltvorgang, mittels der Schülerversuchsspule gemessen.
Aus dem Graphen:
Uind/(ΔI/Δt) = 265/2850 mV·s/mA = 0,092 V·s/A = 0,092 H
|
|
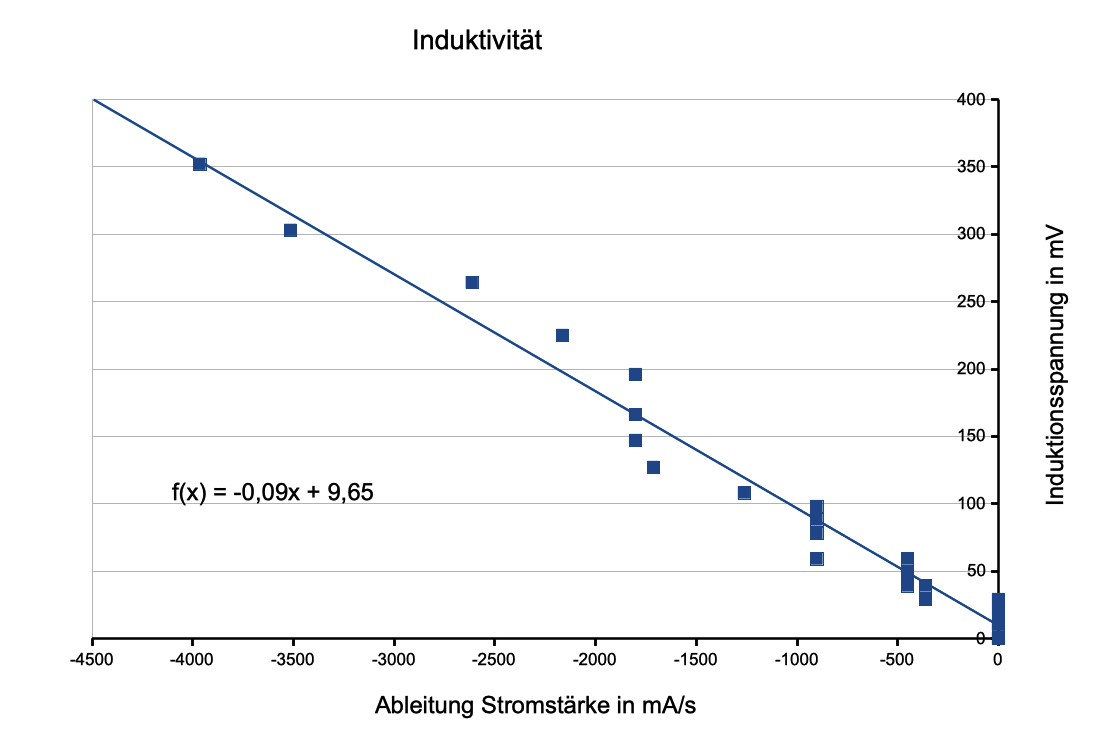
Abb. 5: (Selbst-)Induktionsspannung in Abhängigkeit von der
"Änderungsgeschwindigkeit der Stromstärke" dI/dt beim
Ausschaltvorgang, mittels der Schülerversuchsspule gemessen.
Die Ursprungsgerade kann man halbwegs sicher entnehmen. In beiden
Fällen sollte sich allerdings derselbe konstante Wert der Steigung L
ergeben. Das ist nicht oder nur grob der Fall (hier: 0,092 H bzw.
0,09 H). Die Steigung stimmt auch mit dem Nennwert der Induktivität
nach Herstellerangaben bestenfalls grob überein.
Für die Sch genügt eines der Diagramme von Abb. 4 und 5.
|
Vorgehensweise im Unterricht nach dem Konzept des
"Forschenden Unterrichts"
(PL = Plenum; SV = Schülerversuch,
möglichst "in gleicher Front"; HA = Hausaufgabe)
Selbstinduktion ist den Sch vertraut gemacht
worden, u.a. mit dem Versuch zum "verzögerten Einschalten der Monsterspule"
(630 H) (PL). Deutung als Induktionsvorgang (PL)
SV: Leuchtdiodenversuche
(dort Abb. 12) mit der "Grundschaltung"
zeigen Stromrichtung beim Ein- und Ausschalten an. Die Sch wundern sich,
dass eine LED nie leuchtet ("kaputt?").
PL: Wozu wird in der Grundschaltung R2
benötigt? Hinweis auf SV "Zündfunke"
(dort Abb. 11)
SV: Zeitabhängigkeiten von Stromstärke
und Induktionsspannung nach jeweils einmaliger Energiezuführung zur
Spule werden mit dem ARDUINO registriert und mit dem TBK graphisch
dargestellt.
PL: Sammeln der Ergebnisse:
a) I und Uind hängen in
komplizierter Weise von der Zeit ab. Möglicherweise steckt eine
exponentielle Zeitabhängigkeit dahinter?
b) Beim Einschaltvorgang wird eine solche
Spannung induziert, dass der Strom anfänglich auf 0 gehalten wird. Die
(Selbst-)Induktionsspannung wirkt als "Gegenspannung" entgegengesetzt
zur Batteriespannung UB. Der Betrag der Induktionsspannung
fällt allmählich auf 0 ab, wodurch sie ihre Bremswirkung verliert, so
dass der Strom allmählich einen stationären Maximalwert, den
Sättigungsstrom, erreicht. Beim Ausschaltvorgang hält eine
Spitzenspannung einen kurzzeitig unveränderten Strom durch die Spule, R1
und R2 aufrecht, obwohl die Batterie abgetrennt ist. Es
handelt sich um eine "Mitspannung". Sie sinkt allmählich auf 0 ab, damit
auch der von ihr hervorgerufene Strom. Die Sch könnten vermuten, dass
jetzt I und Uind proportional zueinander sind.
c) Wenn sich I schnell ändert, hat Uind
großen Betrag. Wenn sich I langsam ändert, hat Uind kleinen
Betrag. Der Zusammenhang der "Änderungsgeschwindigkeit von I" (dI/dt)
mit dem Betrag von Uind soll jetzt untersucht werden.
Die Sch formulieren Hypothesen über den
Zusammenhang zwischen U und ΔI/Δt. (Je schneller sich die
Spulenstromstärke I ändert, desto größer ist der Betrag der
Selbstinduktionsspannung.) Sie ergänzen in einem vorbereiteten Diagramm
der TBK den Datenbereich über ein geeignetes Intervall der Messwerte und
erhalten so einen ΔI/Δt-Uind-Graphen, den sie diskutieren.
PL: Formulierung des Ergebnisses: Änderungsgeschwindigkeit
der Stromstärke und Selbstinduktionspannung sind zueinander
proportional, also |Ui| prop. | ΔI/Δt |. Die
Proportionalitätskonstante wird Induktivität L genannt, also |Ui|
= L·| ΔI/Δt |.
PL: Theoretische Deutung mit dem
Induktionsgesetz: Uind = - A·ΔB/Δt. Wenn B prop. I => Uind
prop. - ΔI/Δt, oder mit anderen Worten: Wenn B bis auf einen Faktor = I
ist, dann ist auch Uind bis auf einen Faktor = -
ΔI/Δt). Definition der Induktivität L als Proportionalitätskonstante: L
= | Uind / ΔI/Δt | mit der Einheit 1 V·s/A.
PL/HA: Vermischte
Aufgaben/Abschätzungen (vgl. mit der Theorie):
Qualitative Graphen der Zeitabhängigkeiten von I und Uind mit
den Spitzenwerten der Spannung und den Sättigungswerten der Stromstärke.
Ermittlung der Induktivität L der verwendeten Spule.
Wie würden sich die Spitzenwerte der
Induktionsspannung mit der Frequenz qualitativ verändern, wenn ein
Wechselstrom bestimmter Frequenz und fester Amplitude durch die Spule
geschickt wird?
Technische Bemerkungen
1. Wenn im TBK die Induktionsspannung das
falsche Vorzeichen hat, sollte die Steckeranschlüsse an der
Sekundärwindung der SV-Spule vertauscht werden.
2. Das Schalterprellen lässt sich - besonders
beim Einschalten - kaum vermeiden. Die ersten 2 - 4 Messwerte sind also
kaum brauchbar.
3. Bei der Zeitauflösung des Arduino von ca.
0,1 ms ist es unwahrscheinlich, dass gerade die Spitzenspannungswerte im
"Zeitfenster" der Messung liegen. Sie wird also in der Regel nicht
gemessen. Um keinen falschen Eindruck vom Zeitverlauf der
Selbstinduktionsspannung zu vermitteln, werden die beiden errechneten
Spitzenspannungswerte vom Programm ergänzt.
4. Um das Schalterprellen zu minimieren,
sollte der Taster schnell gedrückt, ruhig gehalten und nach ca. 1 - 2 s
wieder schnell freigegeben werden. Das Arduino-Programm gibt dazu nähere
Anweisungen. Gerade bei den Schaltvorgängen können Störungen
auftreten. Sie können wegdiskutiert werden, oder die Messung wird
wiederholt.
5. Die Induktivität der Schülerversuchsspule
ist in Realität wohl nicht konstant. Der erwähnte Wert von L = 0,1 H =
0,1 Vs/A ist der vom Hersteller angegeben Nennwert. Insbesondere nahe
der Schaltvorgänge scheint sich Uind/(dI/dt) zu ändern und
erst nach ca. 10-20 Messwerten konstant zu werden. Im
Tabellenkalkulationsprogramm wurden deshalb geeignete Bereiche von
Messdaten ausgewählt, die die Proportionalität von Uind und
Steigung der Stromstärke dI/dt halbwegs glaubhaft erscheinen lassen und
die Definition einer Induktivität ermöglichen. Da man solchermaßen ein
zweites Mal etwas mogelt, muss man auch damit rechnen, dass man
streuende Messwerte für L erhält. Dennoch halte ich diesen Versuch für
sehr lehrreich.
6. Die Messwerte, beginnend mit 0,0,0, ... ,
werden kopiert und in das TBK (ODT-Format
bzw. XLS-Format) übertragen,
wobei mitgeteilt wird, dass die Daten durch Kommas getrennt sind. So
werden die Spalten A bis D ausgefüllt. Die übrigen Spalten sind
vorbereitet. Sie sollten nach dem Übertragen der Messwerte in die
Spalten A bis D aktualisierte Werte enthalten. Mit ihnen werden die
Graphen automatisch ergänzt.
Das Programm prog4a_2k
("sketch")
Das Listing finden Sie hier.
Sie brauchen es nur auf dem PC in das Arduino-Fenster (sketches) auf dem
PC kopieren, speichern, hochladen und den Seriellen Monitor in der
oberen Fensterleiste auf dem PC aufrufen. Mit der RETURN- bzw.
ENTER-Taste auf dem PC starten Sie die Messung. Das Listing ist
selbsterklärend.
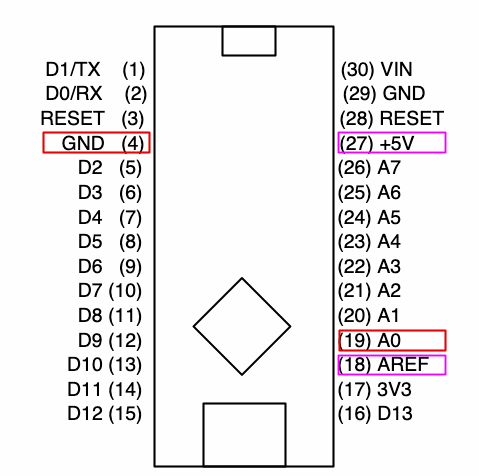 |
Abb. 9:
Anschlüsse des Arduino Nano (Draufsicht Vorderseite)
Die Sch müssen bei der Verbindung der rückseitigen
Steckerpins mit der Messschaltung im Kopf spiegeln! Hier darf
kein Fehler passieren! Die Mess-Schaltung wird über die Pins GND
und z.B. A0 (rot) verbunden.
Es wird die Verwendung eines "under-shields" mit Pegelwandlern zur
Wechselspannungsmessung (Abb. 10) empfohlen
(Pin 27 und Pin 4 könnten zur Spannungsversorgung externer
Schaltungen dienen, z.B. eines Pegelwandlers (OUT), oder zur
Zuführung einer externen Spannung. Zwischen Pin 18 und Pin 4
kann die Referenzspannung für die AD-Wandler gemessen oder auch
von außen zugeführt werden.)
|
|
 |
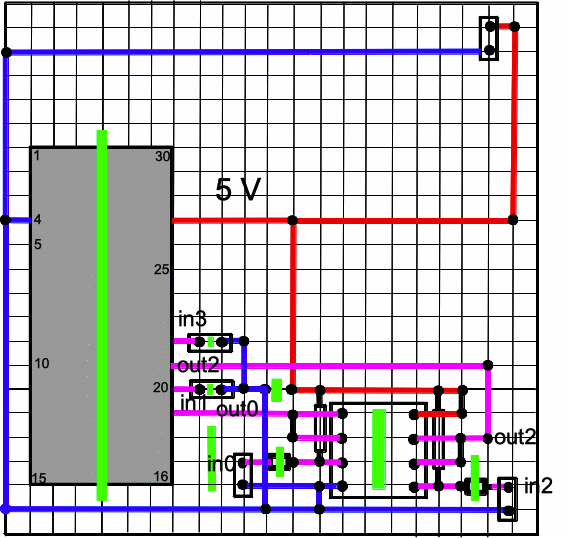
Abb. 10: Das "under-shield", aufgebaut auf einer
Lochraster-Platine. Es stellt - zusätzlich zu 2
Gleichspannungskanälen - einen 2-kanaligen Pegelwandler
zur Wechselspannungsmessung zur Verfügung.
Der ARDUINO wird in den grau gezeichneten Sockel gesteckt, der
2-kanalige Operationsverstärker TLC 272 in den achtpolige Sockel.
Leiterbahn-Unterbrechungen (Draufsicht) sind links grün markiert.
Die Betriebsspannung wird über den ARDUINO aus dem USB-Port
bezogen. Mit dem Steckerpaar rechts oben kann sie weiterverwendet
werden. Die beiden Steckerpaare (in0 und in2, unten) ermöglichen
Wechselspannungsmessungen, die oberen beiden (in1 und in3) nur
Gleichspannungsmessungen.
|
|
ist im
Buchhandel erhältlich.
Viele der dort beschriebenen Versuche für den
Prozessor ATMEGA32 lassen sich auch mit dem Arduino Nano
durchführen, da dieser mit einem ähnlichen Prozessor
ausgestattet ist. Allerdings wird dort als Programmiersprache
AVISE-Forth verwendet. Die Software muss neu geschrieben
werden, was aber relativ leicht möglich ist.
Das Buch beschreibt viele weitere
physikalische Versuche, Unterrichts-Konzepte und nützliche
Details zu ergänzenden Hardware-Komponenten, z.B. zum
Pegelwandler und Schutzdioden.
|
( Januar 2022 )







