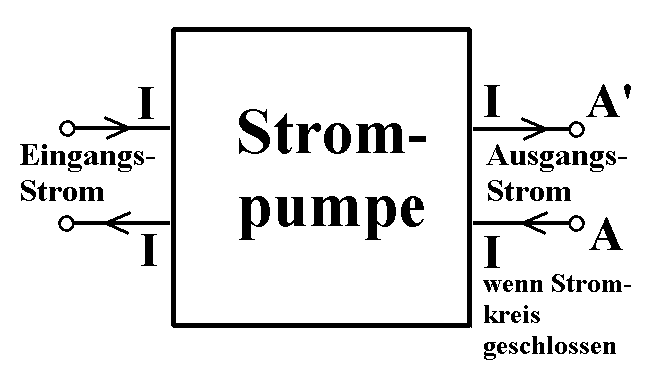Was hat der Arduino mit der Selbstinduktion zu tun?
Das Gesetz
der Selbstinduktion (Uind = - L·ΔI/Δt in einfachen Fällen
- Uind prop. zur "Änderungsgeschwindigkeit der
Stromstärke" (Steigung der t-I-Funktion) ist besonders einsichtig, wenn
man einen Strom I mit abschnittsweise konstanter Steigung ΔI/Δt vorgeben
kann, also einen Dreiecksstrom. I.A. sind zum experimentellen Nachweis
viele Klimmzüge notwendig, da man häufig keinen Einfluss auf die Form des
Stroms hat. Mit einer Strompumpe ist dies aber leicht möglich. Der Arduino
wird dann eingesetzt, um - z.B. im Schülerversuch - den resultierenden
Spannungsverlauf zu registrieren und das Gesetz der Selbstinduktion dem
Experiment zu entnehmen, bzw. die Induktivität sinnvoll zu definieren. Sie
haben richtig gelesen: Ein Strom wird vorgegeben und die resultierende
Spannung gemessen.
Was leistet die Strompumpe für den Physik-Unterricht?
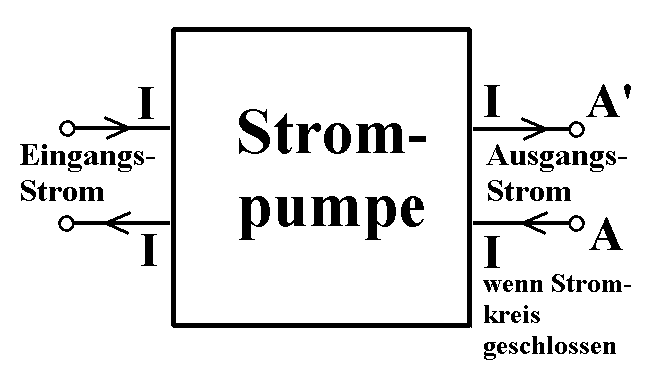 |
Abb. 1: Prinzip einer
spannungsgesteuerten Stromquelle (SGSQ; Strompumpe)
Nach Anschluss eines stromleitenden Bauelements an den
Stromanschluss (Ausgang) wird ein zur Steuerspannung (Eingang)
proportionaler Strom erzeugt, ganz gleich (innerhalb gewisser
Grenzen), welchen Widerstand das Bauelement hat. Ich nenne die
Schaltung manchmal auch "Strompumpe": Ein (links) hinein
fließender Strom wird auch durch den Stromanschluss (rechts)
gepumpt. Bei einem ohmschen Widerstand Re im
Eingangskreis fließt bei einer Dreiecksspannung auch ein dazu
proportionaler Eingangsstrom. Also muss auch im Ausgangskreis (im
Rahmen bestimmter Grenzen) der gleiche dreiecksförmige Strom
fließen, ganz gleich, welches Bauteil im Ausgang angeschlossen
ist.
|
Für den Physik-Unterricht heißt das: Man kann einen bestimmten
Zeitverlauf der Stromstärke durch ein Bauelement vorgeben (!), der
besonders deutlich physikalische Zusammenhänge demonstriert. Als Folge
bildet sich eine Spannung aus, an der das Gesetz des Bauteils "ins Auge
springt". Die Strompumpe sorgt dafür, dass der vorgegebene Strom durch das
Bauteil fließt.
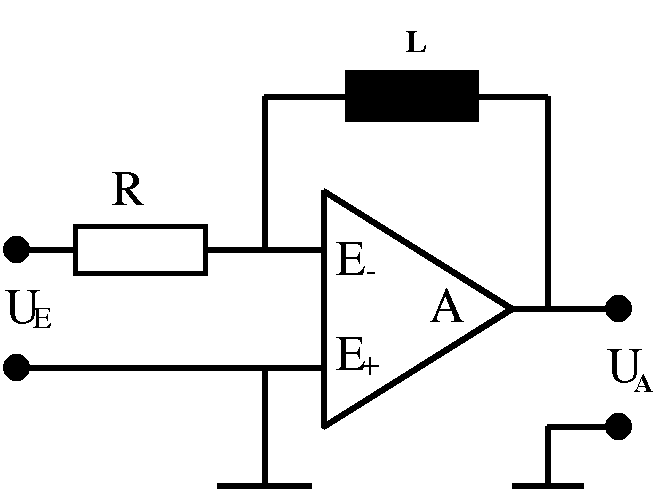
So ist ein dreiecksförmiger Strom durch eine Spule mit einer
abschnittsweise konstanten (Selbst-)Induktionsspannung verbunden. Daran
lässt sich das Gesetz der Selbstinduktion besonders eindrucksvoll
erkennen.
Entsprechend wird auch das Gesetz des Kondensators eindrucksvoll
offenbart, wenn ein symmetrischer rechtecksförmiger Wechselstrom durch
einen Kondensator geschickt wird. Dann bildet sich am Kondensator eine
linear wachsende und fallende Ladespannung aus, also eine dreiecksförmige
Spannung.
Wie die Strompumpe realisiert wird, gar mit Mitteln der
Schülerversuchssammlung, soll vorläufig nicht interessieren.
Über ähnliche Versuche mit anderer Technik wurde schon anderswo
und im Buch des Autors "Physikalische
Schülerversuche mit PC und Mikroprozessor"
berichtet.
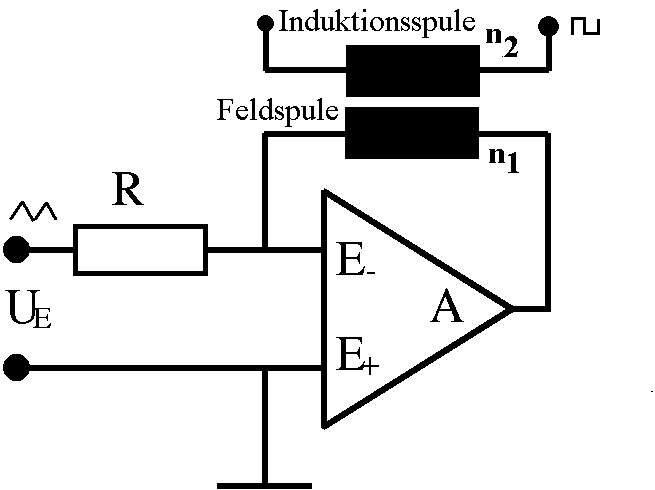
Prinzip der Strompumpe mit einem Operationsverstärker
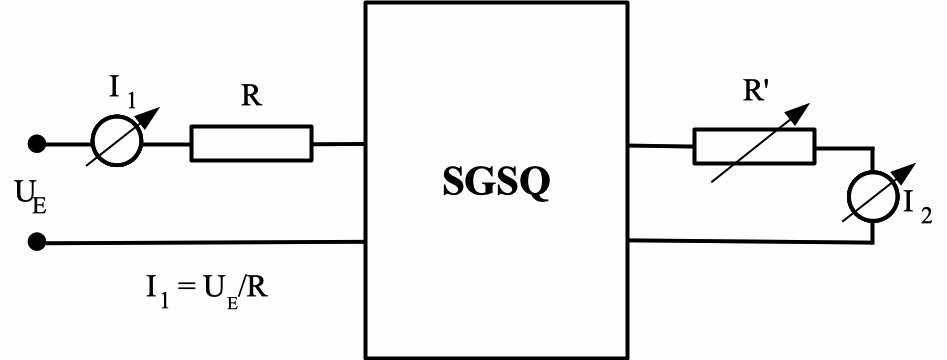
Voraussetzung für den Nutzen der Strompumpe ist, dass im Eingangskreis
und zwischen den Stromanschlüssen (Ausgangskreis) ein gleich großer Strom
fließt. Dies wird mit Amperemetern im Eingangskreis und zwischen den
Stromanschlüssen nach Abb. 3 überprüft. Besonders eindrucksvoll ist es,
wenn im Ausgangskreis ein variabler Widerstand R' eingesetzt wird.
Unabhängig von der Größe von R' fließt (in weiten Grenzen) bei festem
Eingangsstrom derselbe Ausgangsstrom.
Das ist nicht mehr der Fall, wenn 1. der Eingangsstrom den
maximalen Ausgangsstrom des verwendeten OPs
überschreitet, also typisch 10 mA, und wenn 2. die Ausgangsspannung
nicht ausreicht, um den Ausgangsstrom durch Ra zu
pumpen. Die maximale Ausgangsspannung ist etwas kleiner als die
Betriebsspannung des OPs.
Die im Ausgangskreis sich ausbildende Spannung UA ist
i.A. von der Eingangsspannung verschieden und hängt nicht nur von der
"gepumpten" Stromstärke ab, sondern auch vom jeweiligen Widerstand R' im
Ausgangskreis.
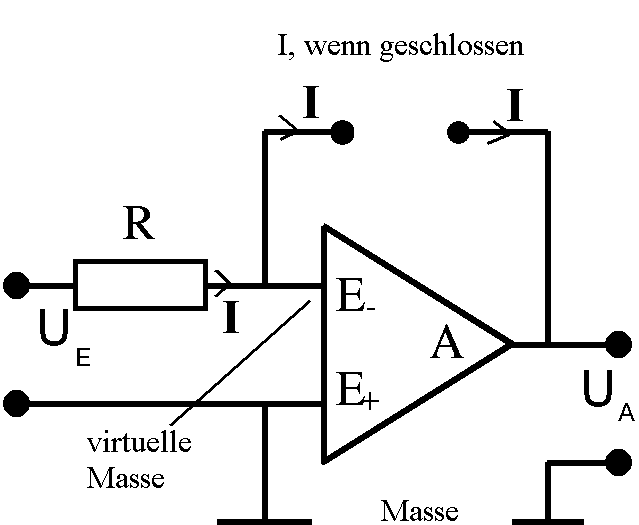
Zu so etwas wie einer "Erklärung" verwendet man
zwei Hilfs-Prinzipien:
1. Virtuelle Masse: Die Spannungen an E- und E+
gegenüber Masse unterscheiden sich bei einem OV im Arbeitsbereich
höchstens um wenige mV. In guter Näherung liegen dann beide Eingänge
"virtuell auf Masse-Potenzial".
(Die Eingangsspannung UE hat dann einen proportionalen
Strom I1 = UE /R durch den Widerstand R zur
Folge.)
2. Stromlosigkeit: Wegen des extrem hohen Eingangswiderstand
kann quasi kein Strom über einen der Eingänge in den OV hinein fließen.
Deshalb muss der Eingangs-Strom durch R über die Stromanschlüsse zum
Ausgang A weiterfließen, also durch das Bauteil zwischen den
Stromanschlüssen.
(Also I1 = I2).
Überprüfung der Strompumpe
Grundgesetz der Spule im Schülerversuch
So, wie das Grundgesetz des ohmschen Widerstands das Ohm'sche Gesetz U =
R·I ist, so ist das des Kondensators Q = C·U bzw. I = C·dU/dt = C·U·
, bzw. in einfachen Fällen I = C·ΔU/Δt, wenn statt der
Zeitableitung der Spannung U· der Differenzenquotient
ΔU/Δt verwendet werden kann. Analog kann auch ein Grundgesetz der Spule
formuliert werden. Es ist das Gesetz der Selbstinduktion Uind =
- L·dI/dt = - L·I·, bzw. Uind = -
L·ΔI/Δt in einfachen Fällen, wenn statt der Zeitableitung der Stromstärke,
I·, der Differenzenquotient ΔI/Δt verwendet werden kann.
Üblicherweise wird es für eine lange Spule theoretisch hergeleitet. Es
könnte bei Ein-/Ausschaltversuchen einer Spule mit ohmschem
Widerstand auch aus einer Messung entnommen werden, wenn man einige Tricks
anwendet.
In einer anderen Situation "springt das Grundgesetz direkt ins Auge",
nämlich, wenn es gelingt, einen Strom durch die Spule zu schicken, der
linear wächst und fällt, einen Dreiecksstrom. Dann ist die Steigung der
Stromkurve, ΔI/Δt, also die "Änderungsgeschwindigkeit von I"
abschnittsweise konstant, ebenso wie Uind. Im allgemeinen
ist das schwer erreichbar. Nicht aber mit einer Strompumpe, bei der man
durch eine Dreiecksspannung einen Dreiecksstrom steuern kann, ganz gleich
durch welche Art von Bauteil, also auch durch eine Spule, jedenfalls in
bestimmten Bereichen der Dimensionierung.
Weitgehend unabhängig vom Widerstand der Spule ist dann ΔI/Δt
abschnittsweise konstant. Wenn das Grundgesetz der Spule erfüllt ist, muss
eine abschnittsweise konstante Induktionsspannung gemessen werden. Der
Quotient Uind / (ΔI/Δt) ist dann die konstante Induktivität L.
Mit dem ARDUINO werden gemäß Abb. 2 die Ausgangsspannung (UA =
Uind) und optional die Eingangsspannung UE (=> I
= UE/R) und gemessen und in Abhängigkeit von t graphisch
dargestellt. Da es sich beidemale um Wechselspannungen handelt, müssen sie
mittels eines zweikanaligen Pegelwandlers
in pulsierende Gleichspannungen umgewandelt werden.
Schätzen wir die Situation quantitativ ab. Die Amplitude der
Eingangswechselspannung sei 2,5 V. Bei R = 1 kΩ folgt ein dreiecksförmiger
Wechselstrom mit der Amplitude 2,5 mA. Er muss auch durch die Spule
fließen. Von Stromminimum zu -maximum haben wir einen Hub von 5 mA. Bei
einer Frequenz von 500 Hz (T = 2 ms) steigt und fällt der Strom jeweils in
einer Halbperiode, also in τ = 1 ms. ΔI/Δt = ΔI/τ = 5 mA/1 ms = 5 A/s. Bei
L = 0,1 H ergibt sich eine Wechselspannung mit der Amplitude Uind
= 0,5 V. Das können wir mit dem ARDUINO noch gut messen. Unsere Strompumpe
kann maximal eine Stromamplitude von typisch 10 mA bewältigen.
Für den Schülerversuch geeignet ist eine billige Schülerversuchsspule
mit 2 Wicklungen über den gleichen Ferritkern mit pro Wicklung mit L = 0,1
H. Durch Beschaltung von 2 SV-Spulen kann man bis zu 0,8 H erreichen.
Induktion und Selbstinduktion in der Schülerversuchsspule
Der Dreiecksstrom durch die Spule führt (im
Idealfall) zu einem abschnittsweise linear wachsenden und fallenden
magnetischen Fluss, der bei der Schülerversuchsspule
den Ferritkern quasi vollständig durchsetzt. Dementsprechend ist die
Selbstinduktionsspannung in der Spule abschnittsweise konstant. Derselbe
sich ändernde magnetische Fluss durchsetzt aber auch die auf den gleichen
Kern gewickelte zweite Spule ("Sekundärspule"), in der eine gewöhnliche
Induktionsspannung entsteht. Beide haben gleichen Betrag. Die
Induktionsspannung ist aber an der Sekundärspule leichter messbar, da sich
die Spannung an der "Primärspule" wegen des (evtl. kleinen)
Spannungsabfalls an ihrem Innenwiderstand (evtl. leicht) von der
Selbstinduktionsspannung unterscheidet. Es bietet sich also an, die
Selbstinduktionsspannung durch die gleich große Induktionsspannung an der
Sekundärspule zu messen.
(Auch bei nicht verschwindendem ohmschen
Widerstand R' der Spule fließt durch die Spule ein dreiecksförmiger
Strom, ebenso wie durch den quasi in Reihe geschalteten ohmschen
Widerstand R. Wegen der Strompumpe ist das hier anders als bei
Ein-/Ausschaltvorgängen in realistischen Stromkreisen mit ihren
exponentiell veränderlichen Strömen.)
Um die Induktionsspannung
mit ihren zwei Vorzeichen mit dem Arduino direkt zu messen,
braucht man auf jeden Fall einen Pegelwandler,
der die Spannungswerte in den positiven Bereich verschiebt, indem eine
konstante Gleichspannung hinzu addiert wird.
Realisierung auf der Leybold-Rastersteckplatte, vor allem
für Schülerversuche
|
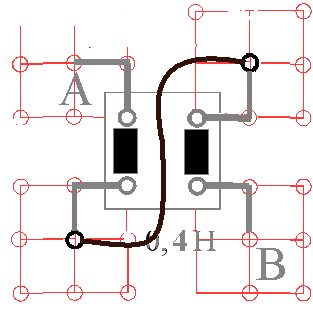 |
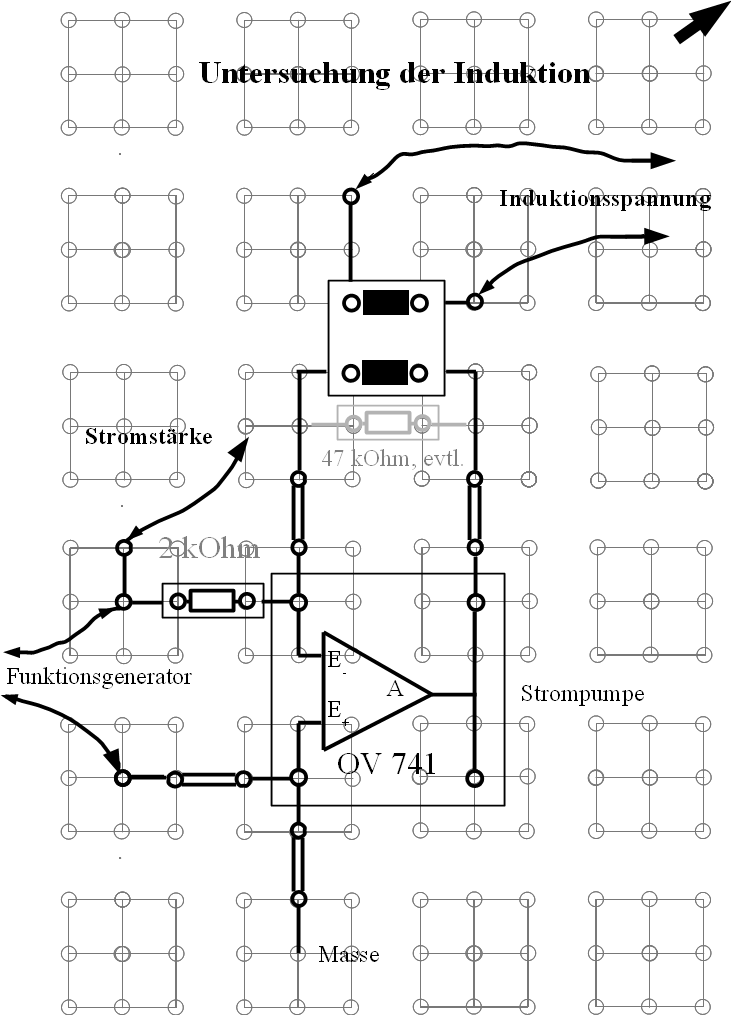
Abb. 6: Strompumpe, periodisch gesteuert durch
Funktionsgenerator: DINA4-Auflageblatt für das
Leybold-Rastersteckbrett zum sicheren Aufbau der Mess-Schaltung
durch die Schüler im SV (Schaltung a). Die Sch stecken die Bauteile
durch das aufgelegte Blatt hindurch. Die rot/grau gezeichneten
"Inseln" (in sich leitend) werden untereinander durch Bauteile oder
leitende Verbindungsstecker (Doppelstriche) verbunden.
Günstiger als der 2 kΩ-Widerstand erscheint ein 1 kΩ-Widerstand
(höhere Stromamplitude, also größere Induktionsspannung).
Die 2. Wicklung der Schülerversuchsspule
kann bei geeigneter Beschaltung zu erhöhter
Induktivität führen oder zur direkten Messung der
Induktionsspannung herangezogen werden.
Auf jeden Fall muss die Induktionsspannung durch einen Pegelwandler
in den nichtnegativen Bereich verschoben wird. Andernfalls droht
Zerstörung des ARDUINO.
Siehe auch Spannungsversorgung |
Abb. 6a: Beschaltung für 4-fache Induktivität
Bei einer Wicklung ergibt sich die Induktivität L = 0,1 H, bei der
Beschaltung oben L = 0,4 H. Mit 2 SV-Spulen kann man bis zu 0,8 H
erzielen.
Bei Beschaltung muss die Induktionsspannung, wie eingezeichnet,
durch die Ausgangsspannung gemessen werden. |
|
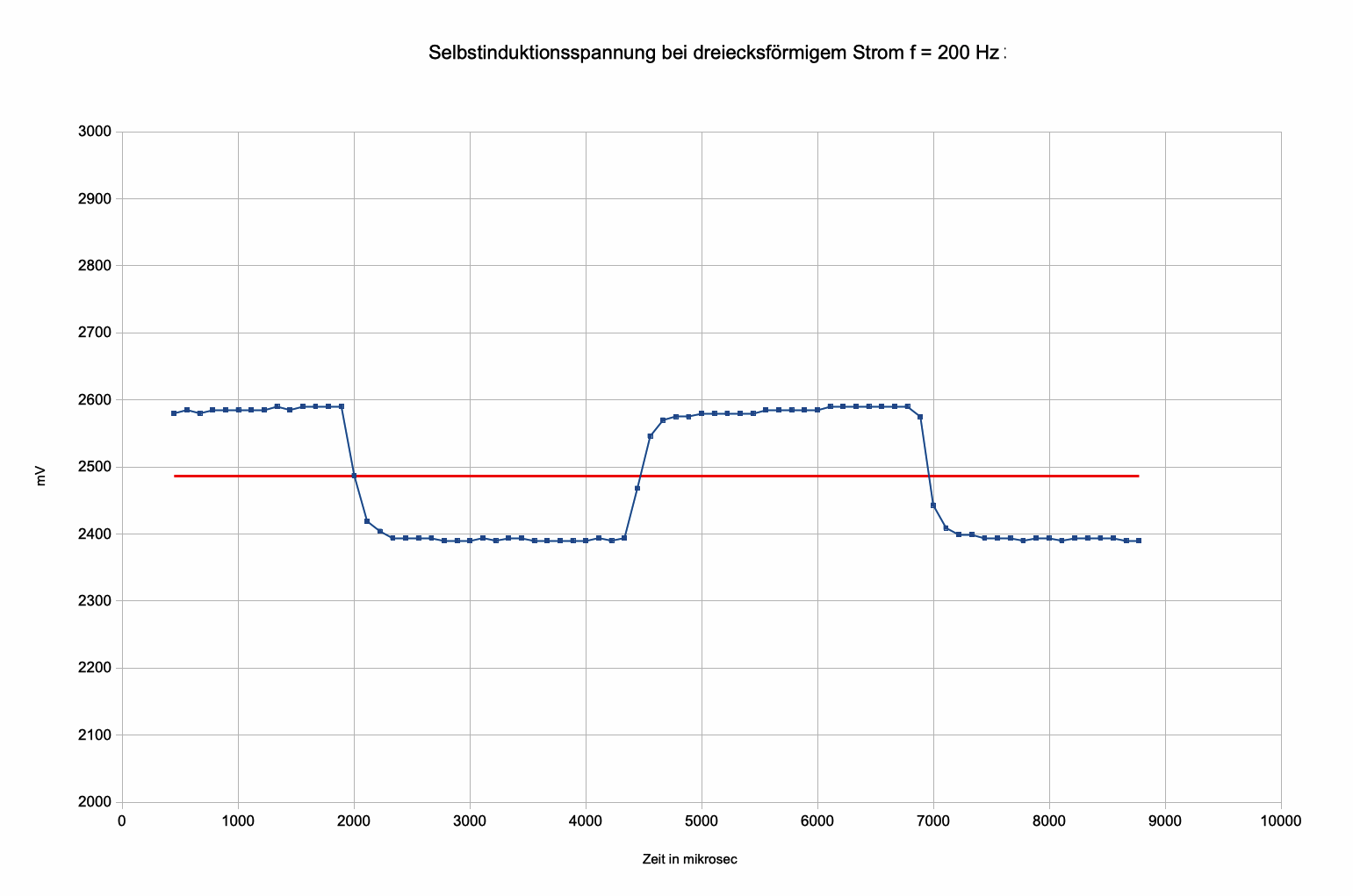
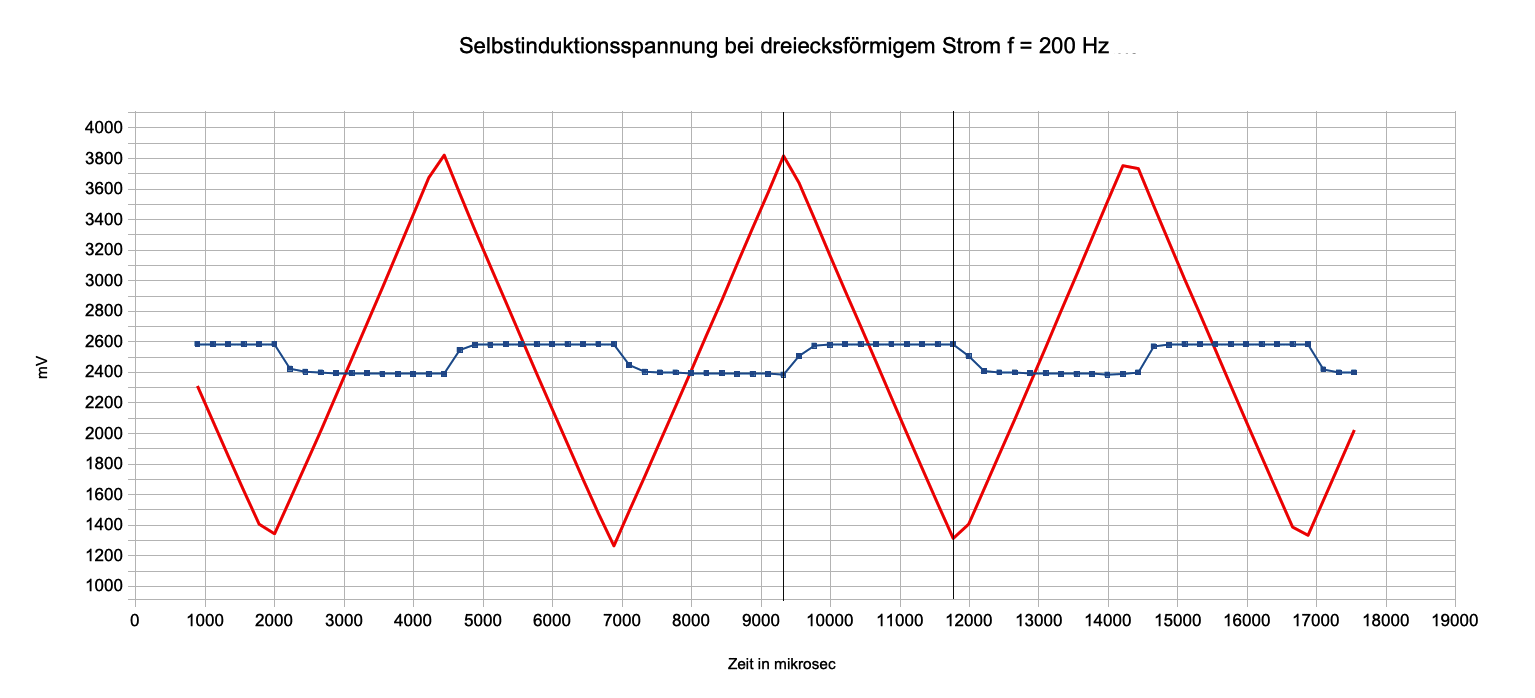
Abb. 7a:
Selbstinduktionsspannung (blau) bei f = 200 Hz und
Eingangsspannung UE prop. Spulenstrom I (rot):
Die Selbstinduktionsspannung bleibt
(abgesehen von Störungen) konstant, solange der Strom linear
wächst oder fällt.
Die gebrochenen
Spitzen der Stromkurve (rot) hängen mit dem endlichen
zeitlichen Auflösungsvermögen zusammen (wegen zweikanaliger
Messung hier nur 0,22 ms pro Messpunkt). Ein Teil der
Rundungen, auch der Spannungskurven, lässt sich so erklären.
Möglicherweise auch braucht der Operationsverstärker wenige
zehntel Millisekunden, bis er den Spulenstrom auf den
Eingangsstrom eingestellt hat.
(In den folgenden Graphen Maßstabsänderung!)
|
|
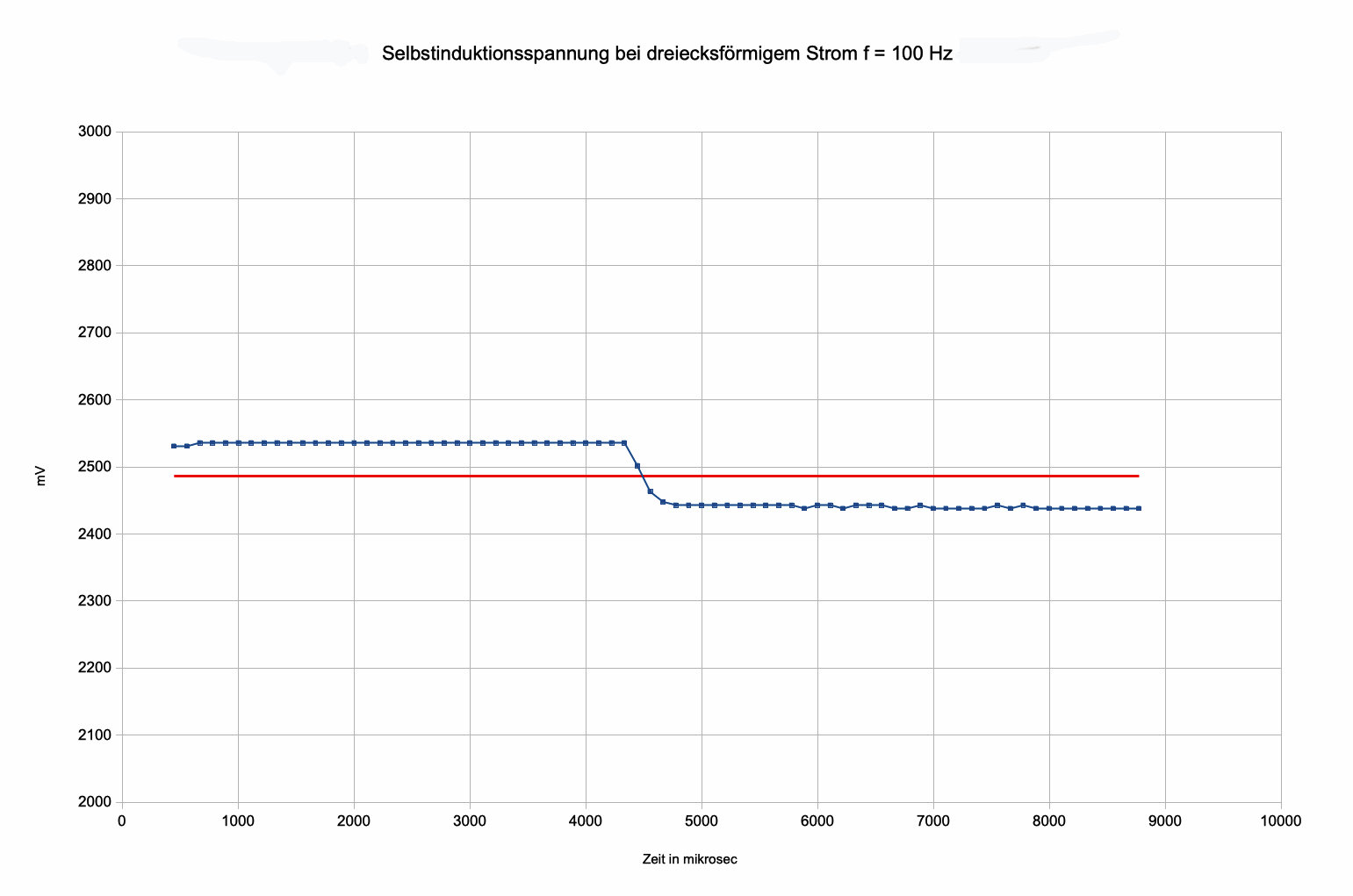
Abb. 7b:
Selbstinduktionsspannung bei f = 100 Hz mit ca. 50 mV
Amplitude
(Messpunkte im Abstand von
0,11 ms; rot: Nulllinie)
Die Selbstinduktionsspannung bleibt
konstant, solange der Strom linear wächst oder fällt.
|
|
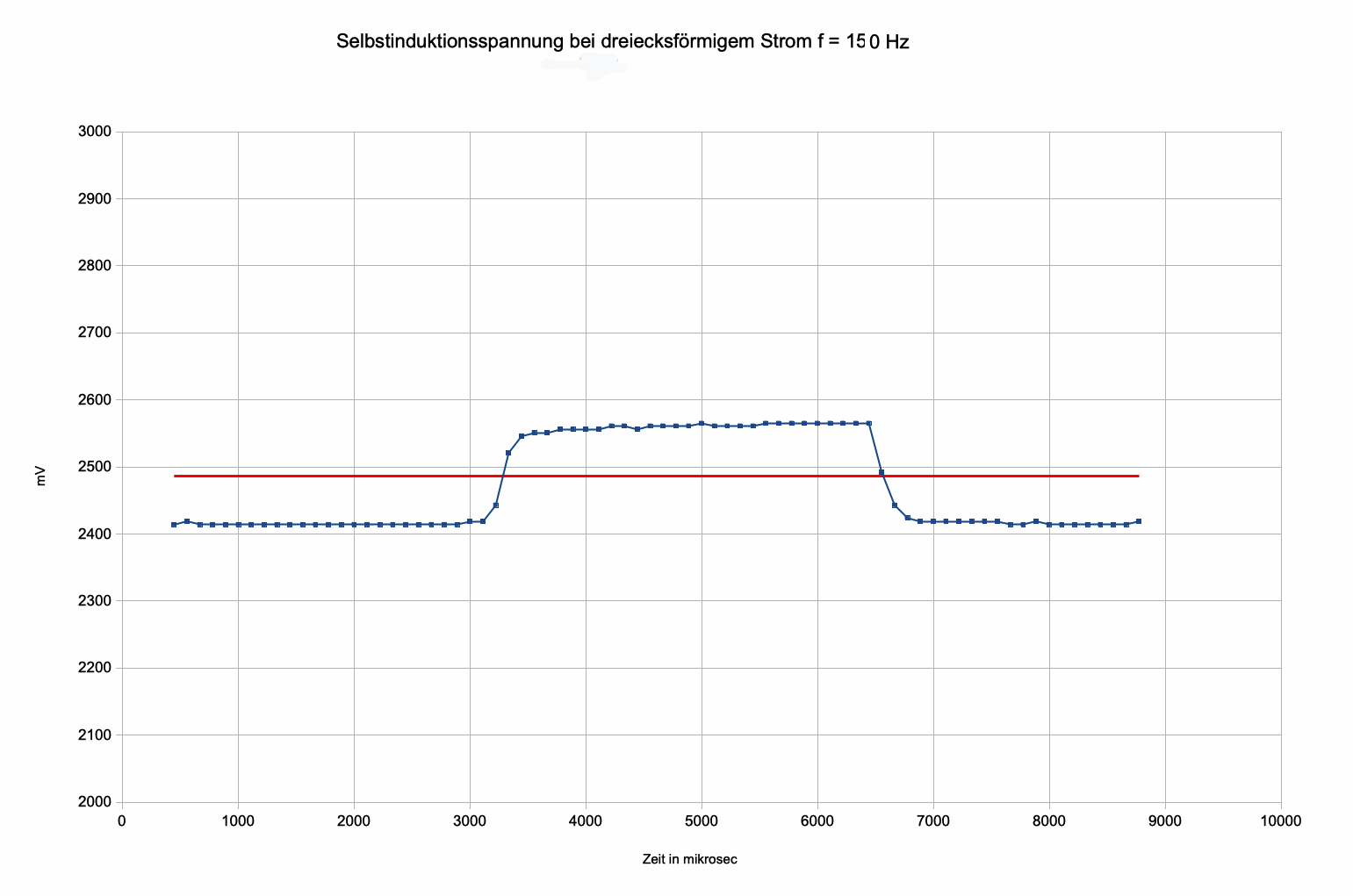
Abb. 7c:
Selbstinduktionsspannung bei f = 150 Hz mit ca. 70 mV
Amplitude
Leichte Schwingungen (nicht
unterdrückt wegen des fehlenden "Dämpfungswiderstands" von 47 k Ω
parallel zur Spule) sind gut tolerierbar. |
Im Prinzip kann durch diese
Messungen L bestimmt werden:
f = 200 Hz: T =
1/200 S = 5 ms Δt = T/2 = 2,5 ms ΔUE
= 5 V => ΔI = 5 mA bei R = 1 kΩ ΔI/Δt = 5
A/2,5 s = 2 A/s => L = ΔUind/ΔI/dt =
0,2 Vs/2 A = 0,1 H
Vielleicht empfinden Sie die Verwendung
eines Funktionsgenerators zur Erzeugung einer Dreiecksspannung als
Komplizierung der Fragestellung oder es steht Ihnen kein
Funktionsgenerator zur Verfügung. Dann können Sie auch einen
einfachen, vom Schüler auf dem gleichen Schaltbrett aufgebauten
handbetätigten Rampen-Generator einsetzen. Dann müssen Sie nur einen
Mess-Sketch bei veränderter Triggerung einsetzen, der den einmaligen
Vorgang registriert.
Der Rampengenerator nutzt die Schaltung
eines Ladungsmessers (auch wieder deutbar als Strompumpe), die einen
Strom durch einen Kondensator pumpt. Solange am Eingang eine konstante
Spannung anliegt, wird (in gewissen Grenzen) der Kondensator durch
einen konstanten Strom geladen. Dabei steigt die Ladespannung linear
an. Die linear veränderliche Ausgangsspannung des Rampengenerators
(bzw. die Kondensatorspannung) dient als Steuerspannung für die
zweite, eigentliche Strompumpe, die einen Dreiecksstrom durch die
Spule pumpt.
Dem Eingangswiderstand des Rampengenerators
wird über einen Taster entweder die Spannung von 2 hintereinander
geschalteten Monozellen oder die positive Betriebsspannung der
Operationsverstärker zugeführt.
Ein erneuter Tastendruck startet eine neue
Messung, aber nur dann, wenn der Experimentator den Kondensator vorher
durch gleichzeitiges Berühren beider Kontakte des Kondensators
entladen hat. Der Körperwiderstand ist genügend groß, um den
Kondensator relativ langsam zu entladen. An der zweiten Strompumpe
entsteht so nur eine geringe Stromänderungsrate ΔI/Δt durch die Spule
und für den ARDUINO werden zu hohe Induktionsspannungen verhindert.
|
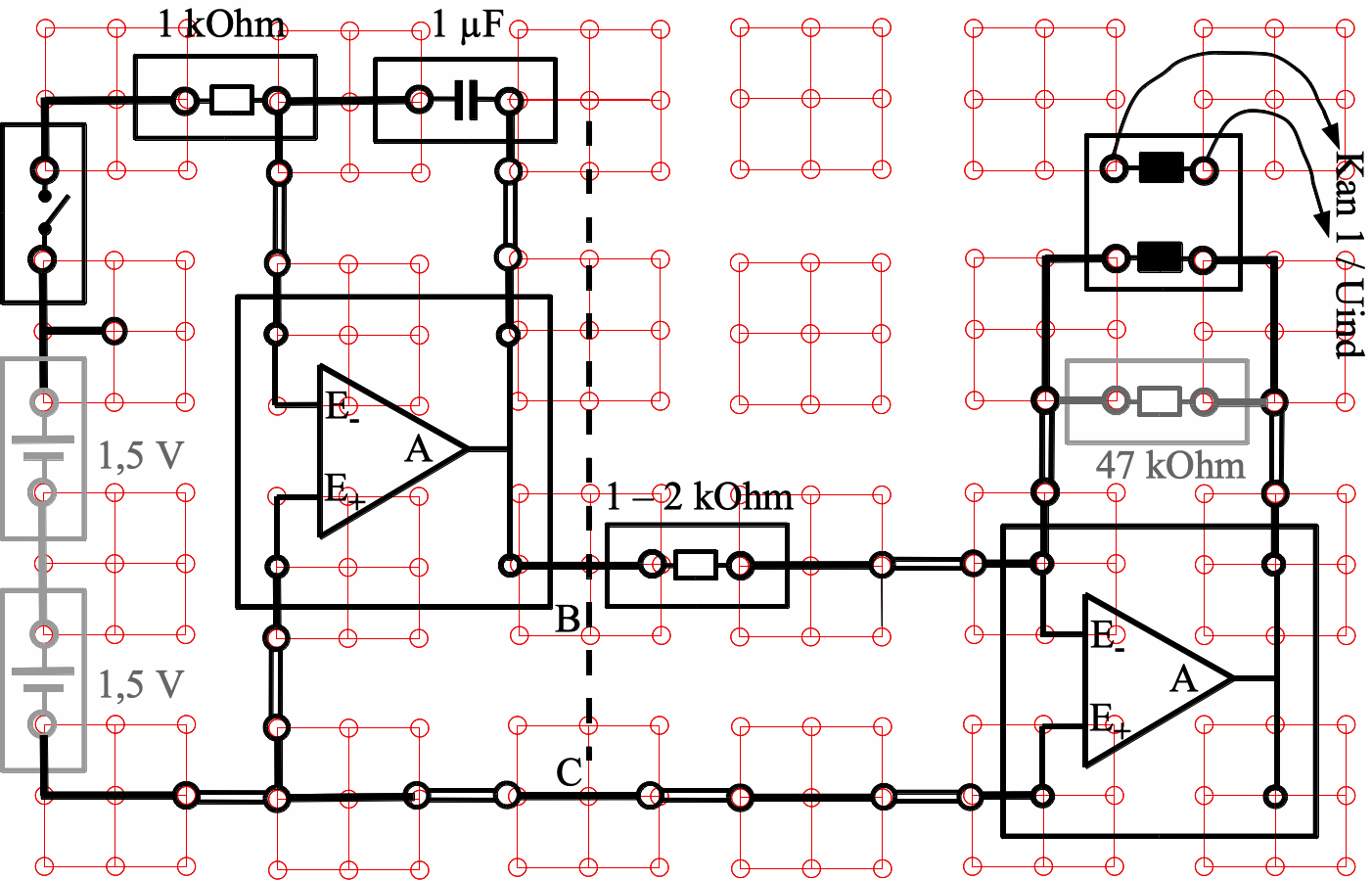
Abb. 8: Strompumpe mit
Rampengenerator (Schaltung b):
DINA4-Auflageblatt für das Leybold-Rastersteckbrett zum sicheren
Aufbau der Mess-Schaltung durch die Schüler im SV. Die
gestrichelte Linie trennt Rampengenerator (links) und Strompumpe
(rechts). Die Eingangsspannung für die Strompumpe könnte
zwischen B und C gemessen werden (Kanal 2).
Auf jeden Fall muss die Induktionsspannung durch einen Pegelwandler
in den nichtnegativen Bereich verschoben wird. Andernfalls
droht Zerstörung des ARDUINO.
Siehe auch Spannungsversorgung |
(PL = Plenum; SV =
Schülerversuch, möglichst "in gleicher Front"; HA = Hausaufgabe)
Selbstinduktion ist den Sch vertraut gemacht
worden, u.a. mit dem Versuch zum "verzögerten Einschalten der Monsterspule"
(630 H) (PL). Deutung als Induktionsvorgang (PL)
SV: Leuchtdiodenversuche
(dort Abb. 12) mit der "Grundschaltung"
zeigen Stromrichtung beim Ein- und Ausschalten an. Die Sch wundern sich,
dass eine LED nie leuchtet ("kaputt?").
PL: Wozu wird in der Grundschaltung R2
benötigt? Hinweis auf SV "Zündfunke"
(dort Abb. 11)
PL: Induktion erfordert einen sich
zeitlich ändernden magnetischen Fluss. Dieser soll durch einen linear
wachsenden und fallenden Strom (einem Dreiecksstrom) durch eine Spule
erzeugt werden. Dazu wird eine Strompumpe vorgegeben. Ihre Funktion wird
mit einigen Gleichstrommessungen nach Abb. 4 getestet. Ergebnis:
Eingangsstrom = Ausgangsstrom. (Auf die Schaltungstechnik soll nicht
eingegangen werden)
SV: Zeitabhängigkeiten von
Induktionsspannung (und evtl. Stromstärke) bei einem
dreiecksförmigen Spulenstrom werden mit dem ARDUINO bei einer festen
Frequenz (z.B. 200 Hz) registriert
PL: Sammeln der Ergebnisse: a) U
konstant, solange sich der Spulenstrom I linear ändert, b) U hat
unterschiedliche Vorzeichen bei wachsenden und fallendem Strom c) Je
schneller sich die Spulenstromstärke I ändert, desto größer ist der
Betrag der Selbstinduktionsspannung. Die Sch formulieren Hypothesen über
den Zusammenhang zwischen U und ΔI/Δt.
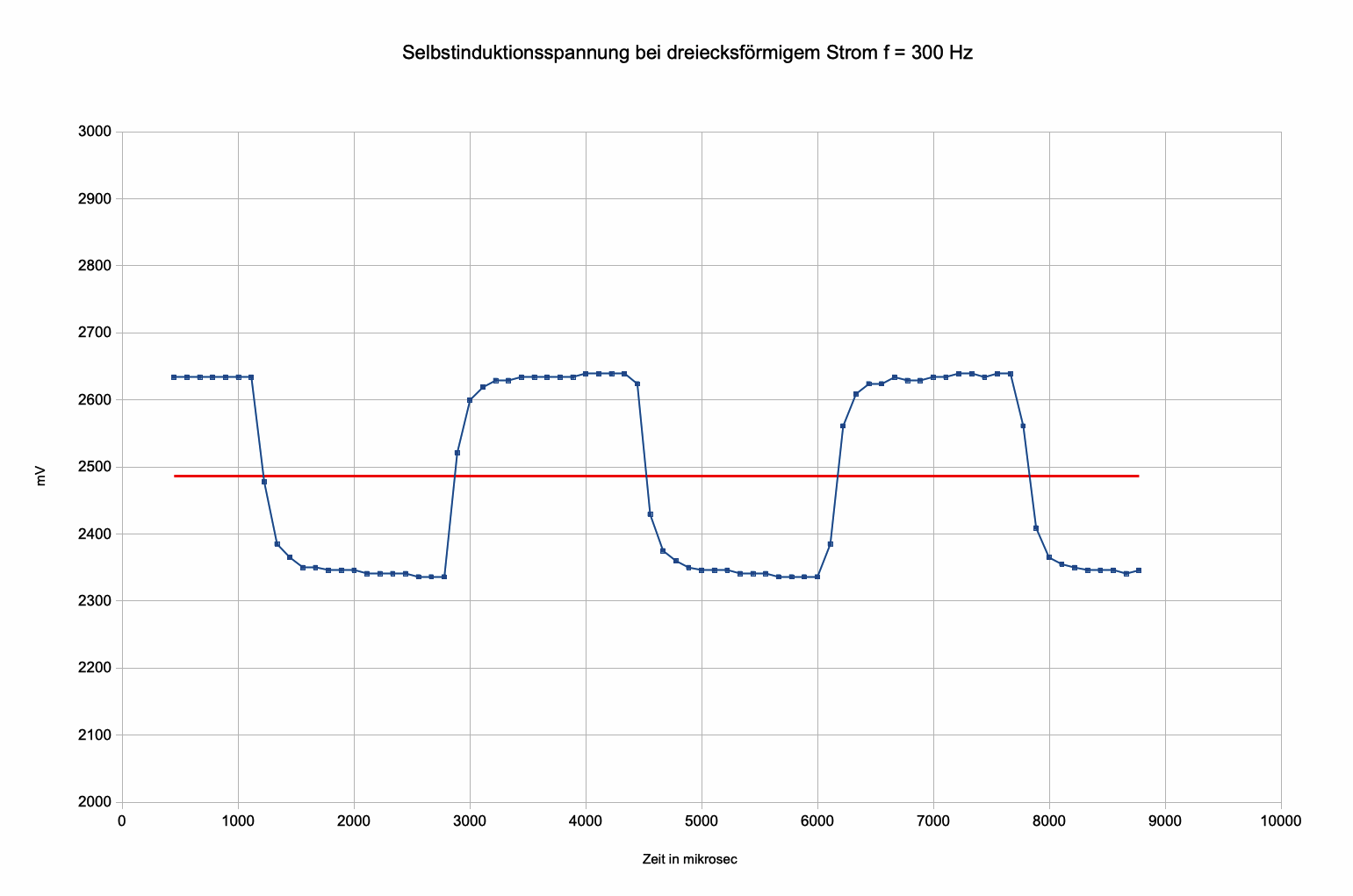
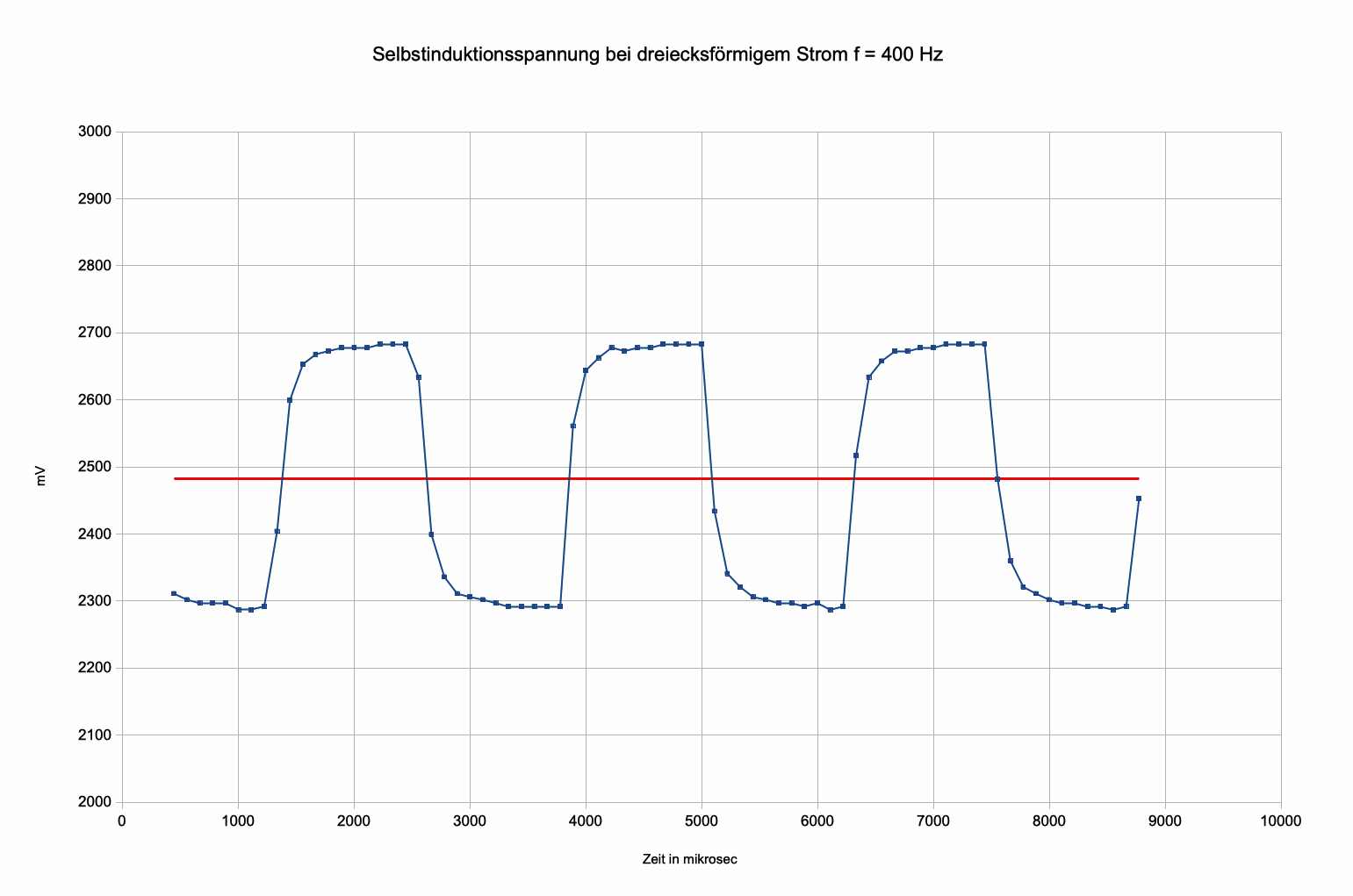
SV: Test der Hypothese bei
unterschiedlichen Frequenzen
PL: Formulierung des Ergebnisses: Änderungsgeschwindigkeit
und Selbstinduktionspannung sind zueinander proportional, also |Ui|
prop. | ΔI/Δt |. Die Proportionalitätskonstante wird Induktivität L
genannt, also |Ui| = L·| ΔI/Δt |.
PL: Theoretische Deutung mit dem
Induktionsgesetz: Uind = - A·ΔB/Δt. Wenn B prop. I => Uind
prop. - ΔI/Δt. Definition der Induktivität L als
Proportionalitätskonstante: L = | Uind / ΔI/Δt | .
PL/HA: Vermischte
Aufgaben/Abschätzungen: Uind in Abhängigkeit von Frequenz,
Änderungsrate von I, und L; Ermittlung der Induktivität L der
verwendeten Spule
Wie kann die Stromänderung erreicht
werden?
a) mit periodischer Dreiecksstrom
Die Sch bauen auf der
Leybold-Rastersteckplatte die Strompumpe nach Schaltung (a) auf. Ein Funktionsgenerator
wird an den Widerstand R am Eingangs angeschlossen.
b) aperiodischer Betrieb mit Rampengenerator
und Strompumpe auf gemeinsamer Leybold-Rastersteckplatte nach Schaltung
(b)
Durch Schließen des Tasters erzeugen die Sch
eine linear wachsende Eingangsspannung für die Strompumpe. Durch
Entladen des 1 µF-Kondensators über die Hand versetzen die Sch den
Rampengenerator wieder in den Ausgangszustand.
c) aperiodischer Betrieb mit Rampengenerator und Strompumpe auf
getrennten Leybold-Rastersteckplatten nach Schaltung (b)
Vielleicht sind Sie der Meinung, dass bei
Schaltung (b) der Kern - die Strompumpe für den Spulenstrom - nicht
genügend klar wird. Dann würde es vielleicht helfen, wenn Sie innerhalb
einer Schüler-Arbeitsgruppe den Rampengenerator und die Strompumpe von
unterschiedlichen Schülern getrennt aufbauen und durch zwei Kabel
verbinden ließen.
Zur Dimensionierung: Bei L = 0,1 H
erzeugt ein Stromänderungsrate ΔI/Δt = 1 A/s eine gerade noch gut
messbare Induktionsspannung von |Uind| = |L·ΔI/Δt| = 0,1 V.
Es sollte also eine Stromänderungsrate von 1 - 10 A/s angestrebt werden.
Bei R = 2 kΩ und einem Hub der Eingangsspannung von 10 V (bei
Spannungsänderung von -5 V bis 5 V; also Stromhub von 5 mA) ergibt sich
bei einer Anstiegszeit τ des Stroms τ = 1 ms eine
Stromänderungsrate ΔI/Δt = 10 mA/1 ms = 10 A/s. Man wird also eine
Anstiegszeit τ des Stroms von typisch 1 ms (oder mehr) anstreben. Beim
Rampengenerator (RG; bei Spannungsänderung von 0 V bis 5 V; also
Stromhub von 2,5 mA) mit C = 1 μF und RRG = 1 kΩ ist τ gerade
RRG·C = 1 ms. Das ist also eine geeignete Dimensionierung.
Mit einem Funktionsgenerator erreicht man τ = 1 ms (halbe Periodendauer)
bei f = 500 Hz, τ = 5 ms bei f = 100 Hz. Dementsprechend nimmt bei sonst
gleichen Daten die Induktionsspannung mit zunehmendem τ ab.
Die Datensätze werden vom PC-Bildschirm des
Arduino eigenen "Serial Monitor" kopiert und in ein
Tabellenkalkulationsprogramm (TBK) übertragen. Das Arduino-Programm
trennt die Ausgabewerte für einen Messwert durch Kommas. Das wird vom
TBK-Programm beim Einfügen der Daten erfragt. Die Messwerte werden in
Abhängigkeit von der Zeit in einem t-x-Diagramm dargestellt. Die Anlage
des Diagramms ist vorbereitet (
ODS-
oder
XLS-Format) und wird nach
Übertragung der Messdaten automatisch ausgefüllt.
Programme ("sketches")
Das Programm 2 bei Verwendung
des Funktionsgenerators
Hier wird nur der Programm-Vorspann gezeigt.
Das vollständige Listing finden Sie unter "prog2p_1k"
oder leicht modifizierbar zu "prog2p_2k".
/*
Liest Daten mit Werten im Bereich von 0 bis
1023 vom ANALOG INPUT Kanal A0 (oder optional zusätzlich A2) ein,
mit oder ohne Pegelanhebung für Wechselspannung, und speichert sie
schnell im SRAM des Prozessors ab.
Dazu wird durch eine spezielle Triggerung in Kanal A0 dafür gesorgt,
dass die Registrierung der Messwerte nach einem Tastendruck beim PC mit
dem Abfall der Messspannung aus ihrem Maximalwert beginnt.
Die Daten werden als Paket von 300 Werten auf 5000 mV (bzw. an die an
PIN18 des ARDUINO liegende
Vergleichsspannung) skaliert und dann seriell an den Serial Monitor
ausgegeben.
In der Mess-Schaltung wird die Dreiecksspannung eines
Funktionsgenerators an den Eingang einer Strompumpe gelegt
(Eingangswiderstand 1 - 2 kΩ, z.B. Schülerversuchsspule mit L =
0,1 H).
Bei Verwendung von zweien dieser Bausteine sind Induktivitäten bis 0,8 H
erreichbar. Bei Verwendung der Schülerversuchsspule
kann die Induktionsspannung auch mittels der 2. Wicklung gemessen
werden.
Bei einkanaliger Messung wird für einen
Messwert ca. 0,11 ms benötigt, bei zweikanaliger Messung für ein Paar
von Messwerten ca. 0,22 ms.
Basis der Programmierung war ein
Beispielprogramm:
http://www.arduino.cc/en/Tutorial/AnalogInOutSerial
*/
b) Zur
Triggerung bei Verwendung des Rampengenerators
a) Schleife bis Induktionsspannung = 0
b) Schleife solange Induktionsspannung = 0
c) Messungen für Stromanstieg bis (evtl.
halbe) Maximalzahl der Messwerte erreicht
Evtl. dann noch einmal entsprechend a) bis c)
für den Stromabfall.
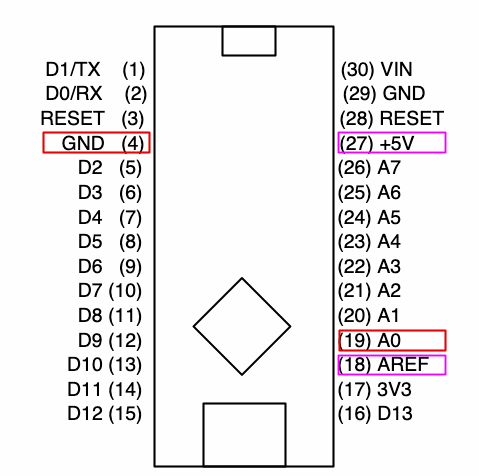 |
Abb. 9:
Anschlüsse des Arduino Nano (Draufsicht Vorderseite)
Die Sch müssen bei der Verbindung der rückseitigen
Steckerpins mit der Messschaltung im Kopf spiegeln! Hier darf
kein Fehler passieren! Die Mess-Schaltung wird über die Pins GND
und z.B. A0 (rot) verbunden.
Es wird die Verwendung eines "under-shields" (Abb. 10) empfohlen
(Pin 27 und Pin 4 könnten zur Spannungsversorgung
externer Schaltungen dienen, z.B. eines Pegelwandlers (OUT),
oder zur Zuführung einer externen Spannung. Zwischen Pin 18 und
Pin 4 kann die Referenzspannung für die AD-Wandler gemessen oder
auch von außen zugeführt werden.)
|
|
 |
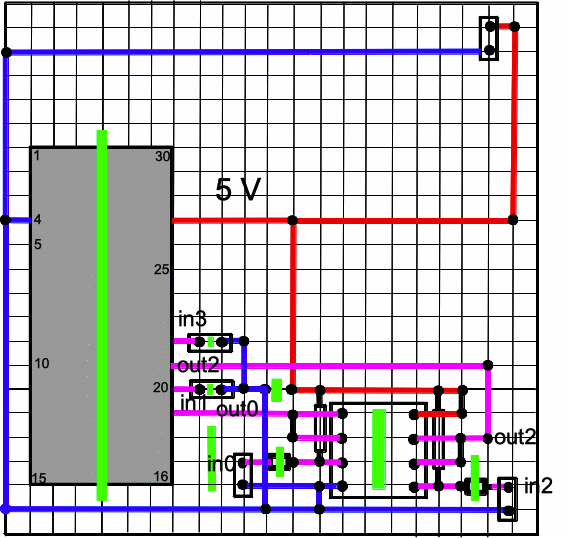
Abb. 10: Das "under-shield", aufgebaut auf einer
Lochraster-Platine. Es stellt - zusätzlich zu 2
Gleichspannungskanälen - einen 2-kanaligen Pegelwandler
zur Verfügung.
Der ARDUINO wird in den grau gezeichneten Sockel gesteckt, der
2-kanalige Operationsverstärker TLC 272 in den achtpolige Sockel.
Leiterbahn-Unterbrechungen (Draufsicht) sind links grün markiert.
Die Betriebsspannung wird über den ARDUINO aus dem USB-Port
bezogen. Mit dem Steckerpaar rechts oben kann sie weiterverwendet
werden. Die beiden Steckerpaare (in0 und in2, unten) ermöglichen
Wechselspannungsmessungen, die oberen beiden (in1 und in3) nur
Gleichspannungsmessungen.
|
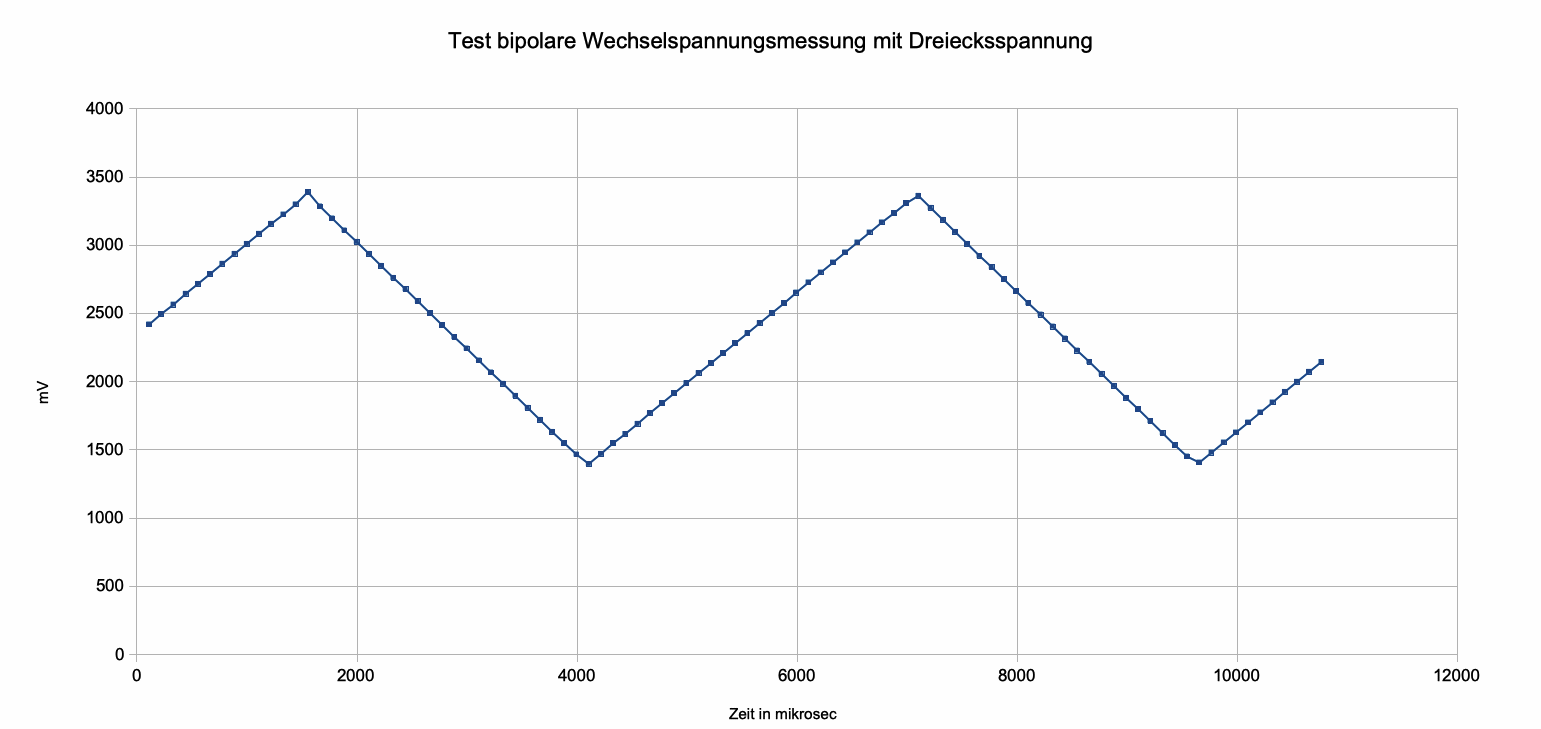 |
Abb. 11: Test
des schnellen Messprogramms mit ca. 9000 Messungen pro s
mit einer Dreiecksspannung von ca. 170 Hz
Die ungleichmäßigen Ecken entstehen dadurch, dass die gezeichneten
Messpunkte im minimalen Zeitabstand von 0,11 ms miteinander
verbunden wurden (pro Periode typischerweise ca. 51 Messungen).
Schneller geht es wohl mit dem verwendeten Prozessor nicht.
Das Programm ist z.B. auch geeignet bis zu einigen 100 Hz.
T = 0,005 s => f = 200 Hz |
Nicht eingezeichnet ist in allen
Schaltungen mit dem OV der Abb. 3 - 8 die bipolare
Spannungsversorgung
des Operationsverstärkers (U
B typisch +/- 5 V oder +/-
12 V)
|
ist im
Buchhandel erhältlich.
Viele der dort beschriebenen Versuche für den
Prozessor ATMEGA32 lassen sich auch mit dem Arduino Nano
durchführen, da dieser mit einem ähnlichen Prozessor
ausgestattet ist. Allerdings wird dort als Programmiersprache
AVISE-Forth verwendet. Die Software muss neu geschrieben
werden, was aber leicht möglich ist.
Das Buch beschreibt viele weitere
physikalische Versuche, Unterrichts-Konzepte und nützliche
Details zu ergänzenden Hardware-Komponenten, z.B. zum
Pegelwandler und zu Schutzdioden für ihn.
|
Bzgl. des Rampengenerators habe ich
möglicherweise vor Jahrzehnten von Prof. Dr. D. Heuer gelernt.
(Juni / Dezember 2021)