Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Wie löse ich physikalische Aufgaben?

Überholvorgang

Aufgabe:

Hilfreich ist es dabei besonders, wenn Du darauf getrimmt bist, die Grundgleichungen für Zeitintervalle (Δt) zu verwenden. Alle bisher behandelten Fälle sind danach in den beiden Grundgleichungen enthalten:

Δv  = a · Δt	v = v0 + Δv
Δx = v0 · Δt + ½ · a · Δt2	x = x0 + Δx

oder nach dem PUB (Prinzip der Unabhängigkeit der Bewegungen):

x = x0  +   v0 · Δt + ½ · a · Δt2

v =            v0          +    a · Δt

Dabei sind x₀ und v₀ Anfangsort und Anfangsgeschwindigkeit zu Beginn des jeweiligen Intervalls Δt.

a) Aufstellen eines Ansatzes anhand eines Graphen	Will man eine solche Aufgabe nicht als reine Algebra-Aufgabe aufziehen, muss man sich die physikalischen Ansätze anhand eines Graphen überlegen: Die Ansätze ergeben sich daraus ganz automatisch und sicher
Dazu ist es notwendig, zuerst ein Koordinatensystem zu wählen:	Die Richtung, in die sich beide Fahrzeuge bewegen, soll die positive Richtung sein (x-Koordinaten sind positiv und wachsen in diese Richtung). Der Koordinatenursprung soll an der Ampel beim Umschalten auf Grün sein. Beide Fahrzeuge befinden sich also zur Zeit 0, beim Umschalten, am Ort 0. Eine solche oder ähnliche Wahl ist immer notwendig, aber vielfach auch selbstverständlich.
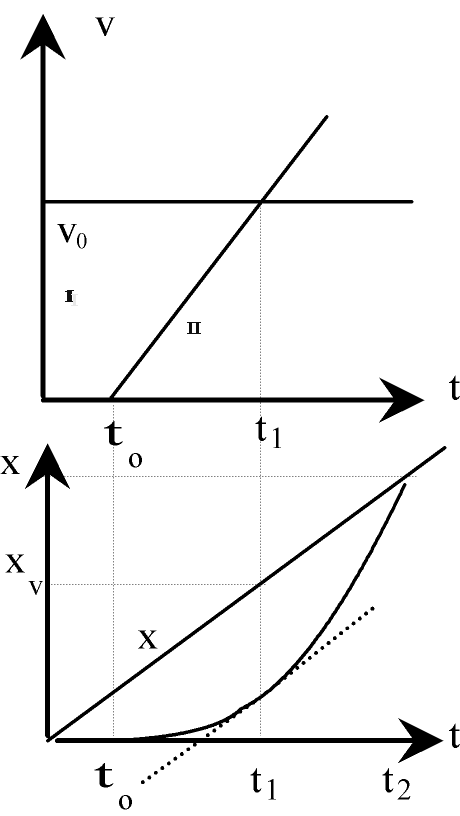	Das ist vielleicht der schwierigste Teil der Aufgabe: richtige Graphen zu skizzieren. Nur wenn sie die betreffende Bewegung richtig wiedergeben, hast Du eine Chance zur Lösung: Der Graph des Radfahrers im t-v-Diagramm ist eine Parallele zur t-Achse bei der Geschwindigkeit v0. Bis zur Zeit t = t0 ruht der PKW ( v = 0). Von da an beschleunigt er gleichmäßig: Von da an muss seine Geschwindigkeit linear wachsen mit der konstanten Steigung a. Im t-x-Diagramm muss der Graph des Radfahrers eine Ursprungs-(Halb-)Gerade sein. Ihre Steigung ist gerade die konstante Geschwindigkeit v0. Bis zur Zeit t = t0 ruht der PKW am Ort x0 = 0. Der Graph verläuft also im t-x-Diagramm auf der Zeitachse bis zu t0. Von da an beschleunigt der PKW. Von jetzt ab ist also der t-x-Graph ein Ast einer Parabel mit dem Scheitel bei t0 (weil dort v = 0 ).
Für den Radfahrer liest Du für seine Geschwindigkeit vR aus dem t-v-Diagramm ab: (1)    vR = v0 = konst. und aus dem t-x-Diagramm für seinen Ort: (2)    xR = v0 · t	Für den PKW ("Auto A"):       vA = 0            für 0 < t < t0:                        hier steht der PKW ja noch ! (3)  vA = a ( t - t0)   für    t0 < t:                          hier beschleunigt der PKW                            gleichmäßig! Für die Bewegung im zweiten Zeitintervall ist - bezogen auf den Intervall-Anfang  - also Δt = t - t0 zu setzen. Aus dem t-x-Diagramm folgt:        xA = 0     für      für 0 < t < t0 und (4)   xA = ½ ·a · (t - t0 )2   für  t0 < t
Gleiche Geschwindigkeit (Bedingung: gleiche Geschwindigkeit) zur Zeit  t1 erhält man also für  (1) = (3): v0 = a ( t1 - t0) Daraus erhält man also  t1 = t0 + v0 / a	Mit (2) ergibt sich damit  xR = v0 . (t0 + v0/a) und mit (4): xA = ½ · a (t0 + v0 / a - t0 )2 = v02 / 2a woraus sich leicht der Abstand d bei gleicher Geschwindigkeit errechnen lässt (der Radfahrer ist immer noch voraus): d =  xR - xA =  v0 · (t0 + v0/a) - v02 / 2a d =  v02 / 2a + v0·t0
Den Zeitpunkt der Begegnung (Bedingung: gleicher Ort) erhält man aus (2) = (4), also        v0 . t2   = ½ · a · (t2 - t0 )2 Dies führt - nach Multiplikation mit 2/a zu einer quadratischen Gleichung für t2 : (t2 - t0 )2 - 2 · v0 /a · t2  = 0   bzw. t2 2  - 2· t2 ( t0 + v0/a ) +  t02 = 0 Mit der Lösungsformel kannst Du die quadratische Gleichung leicht selbst lösen. Es sollte herauskommen: t2  = t0 + v0/a + √( (v0/a) 2 + 2 · v0/a · t0   )	.
Erst jetzt werden Zahlenwerte eingesetzt. Das sollte aber in der 11. Klasse reine Routine für Dich sein.	Du solltest erhalten: a) Zur Zeit t1 = 1,8 s, also 1,8 s  nach dem Umschalten auf Grün haben beide Fahrzeuge gleiche Geschwindigkeit. b) Zur Zeit t2 = 3,4 s, also 3,4 s  nach dem Umschalten auf Grün passiert der PKW gerade den Radfahrer.

Hinweis:

Der Ausgang von den Zeitintervallen (Δ t)  führt unmittelbar zur Verwendung der richtigen Zeitdifferenzen! Es gibt dann keine Verwechslungsmöglichkeit zwischen den Zeitpunkten gleicher Geschwindigkeit und gleichen Ortes!

Denke Dir ähnliche Vorgänge aus und übe zunächst nur, die zugehörigen Graphen richtig zu zeichnen. In einem Fall könntest Du dazu auch einen Ansatz machen und die Rechnung durchführen.

So ähnlich geht der Lehrer bei der Entwicklung einer Schulaufgabe auch vor: Er geht von besprochenen Aufgaben aus und ändert sie ab, so dass er sieht, dass Du den Kern der Sache verstanden hast, ohne den Lösungsweg auswendig gelernt zu haben.

.

.