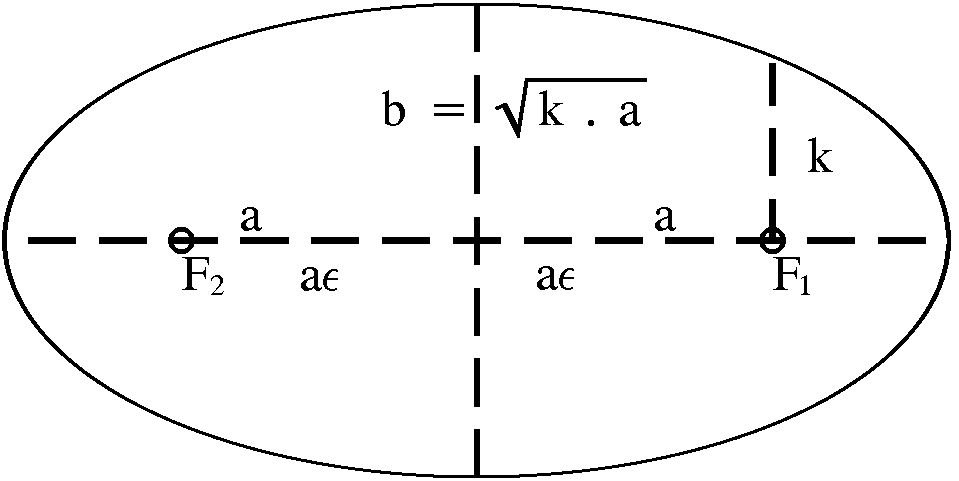Physik-Lernen mit dem Computer: KEPLER

Download PC-Programm (Win32) KEPLER

ZIEL:
BESCHREIBUNG:
FRAGESTELLUNGEN:
EINSATZMÖGLICHKEITEN:
HINWEISE ZUM EINSATZ:
TYPISCHE VERSUCHSERGEBNISSE:
MENÜPUNKTE
ZUR THEORIE DER KEPLERBEWEGUNG:
LITERATURHINWEISE:

Messung von Bahnparametern (hier k)

Mit Hilfe des bekannten Kraftgesetzes wird die Bewegung eines oder mehrerer Planeten auf dem Bildschirm simuliert. Es können die Parameter Energie, Flächengeschwindigkeit (Drehimpuls), Exzentrizität und Halbachse, Planetenname und das Kraftgesetz verändert werden. "Experimentell" sollen die Kepler-Gesetze ermittelt und veranschaulicht werden. Dadurch, dass alle Parameter frei wählbar sind, können Sie sich ihren eigenen "Planeten" schaffen. Das ist insbesondere dann nützlich, wenn der Flächensatz behandelt wird, weil man dann sehr exzentrische Bahnen wählen kann.

BESCHREIBUNG: zurück

Ausgehend von dem Kraftgesetz und bestimmten Anfangsbedingungen bzw. einer gewählten Flächengeschwindigkeit (Drehimpuls) wird die Bewegung eines Planeten nach der "Methode kleiner Schritte" simuliert. Kann der Zeitschritt für verschiedene Bewegungen konstant gewählt werden, so kann der Realzeit-Ablauf der Bewegungen am Bildschirm verglichen werden. In jedem Fall läuft die Anzeige einer Uhr mit, so daß auch bei variablen Schrittweiten die Umlaufdauer korrekt ermittelt werden kann. Im Prinzip kommt man bei fast kreisförmigen Bahnen schon mit wenigen Schritten pro Umlauf aus. Erst bei sehr stark elliptischen Bahnen muß die Zahl der Schritte pro Umlauf u.U. drastisch erhöht werden. Bei heutigen Rechnergeschwindigkeiten wird die Bewegung hinreichend langsam, wenn man als Schrittzahl z.B. 10000 für alle Planeten festlegt. Wegen der Integration der Bewegungsgleichung läßt sich das Kraftgesetz leicht verändern und es kann auch die Wirkung anderer "Gravitationsgesetze" erprobt werden. Die charakteristischen Größen der Keplerbahnen können mit der Maus vermessen werden.

FRAGESTELLUNGEN: zurück

Ermittlung der 3 Kepler-Gesetze Vergleiche von Planetenbahnen Informationen über die Planeten und ihre Monde Vergleich von Planetenbahnen zu gleichen Energien, aber unterschiedlichen Flächengeschwindigkeiten Vergleich von Planetenbahnen zu gleichen Flächengeschwindigkeiten, aber unterschiedlichen Energien Welchen Einfluß hat die Energie auf die Bahnform, speziell auf Halbachse und Exzentrizität? Welchen Einfluß hat die Flächengeschwindigkeit (der Drehimpuls) auf die Bahnform, speziell auf Exzentrizität und Halbachse? Wie würden die Planetenbahnen verlaufen, wenn das Kraftgesetz durch eine andere Potenz des Abstands gegeben wäre?

EINSATZMÖGLICHKEITEN: zurück

Veranschaulichung und "experimentelle" Ableitung der Kepler-Gesetze in der Mechanik der 11. Klasse; Demonstrations"versuch" oder Schüler"versuch" oder häuslicher Schüler"versuch" am schülereigenen Rechner; Vorbereitung von Kurzreferaten

HINWEISE ZUM EINSATZ: zurück

Z.B. mit der Hardcopy-Funktion läßt sich der Bildschirm auch ausdrucken und den Schülern auf einem Arbeitsblatt mitgeben.

TYPISCHE VERSUCHSERGEBNISSE: zurück

Nicht geschlossene Planetenbahnen beim Kraftgesetz r^-2+ß, wobei ß = 0,2

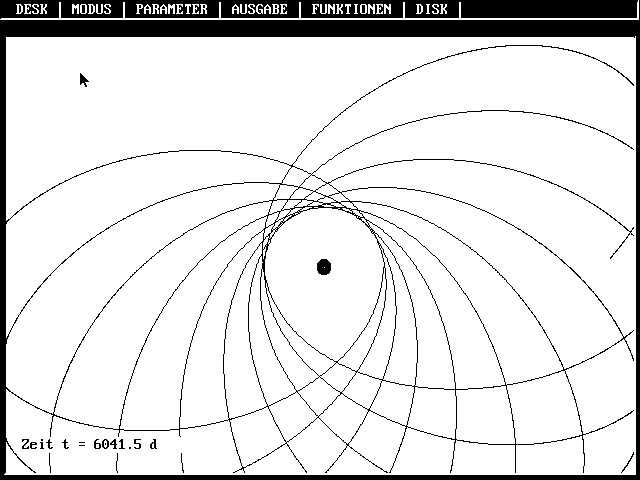Nicht geschlossene Planetenbahnen beim Kraftgesetz r^-2+ß, wobei ß = - 0,1

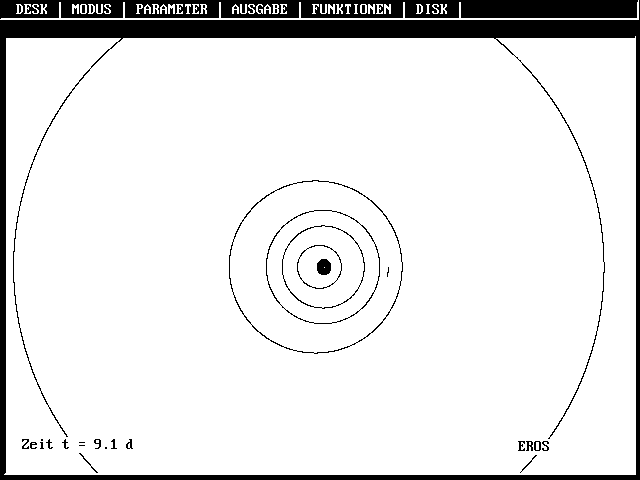Bahnen der Planeten Merkur bis Jupiter Bahnen der Planeten Merkur bis Jupiter und der Planetoiden Eros, Ceres, Adonis, Ikarus und Hidalgo

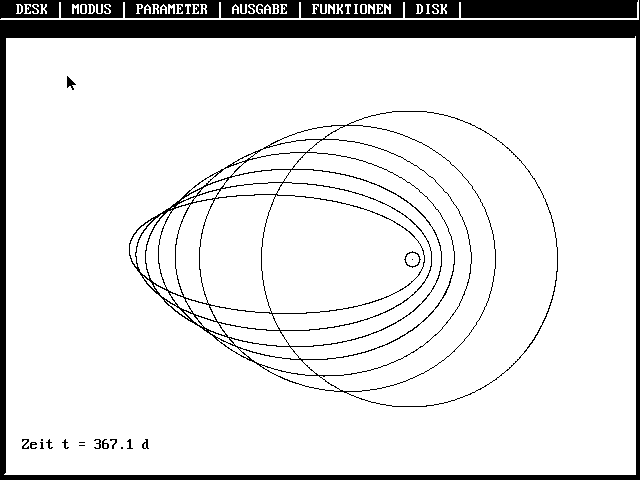Bahnen gleicher Energie pro Masseneinheit (mit zunehmender Flächen-
geschwindigkeit (Drehimpuls pro Masseneinheit) wächst die numerische
Exzentrizität

Bahnen gleicher Flächengeschwindigkeit (mit abnehmendem Betrag der
Energie wächst die große Halbachse)

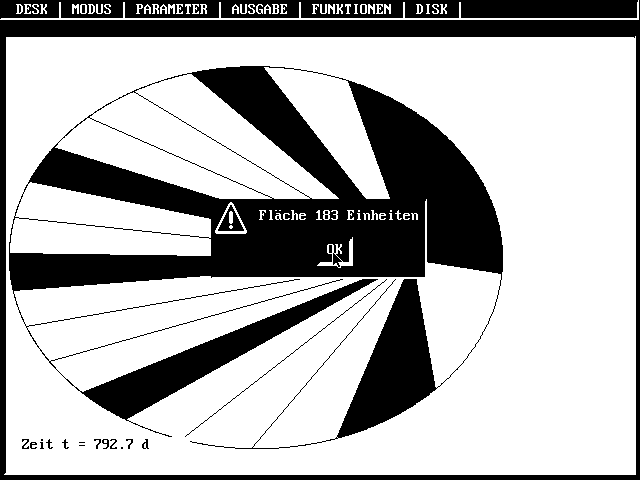Beim Schwärzen der Flächen werden die Pixel gezählt und so das 2.
Kepler-Gesetz bestätigt

MENÜPUNKTE zurück

I DESK I.1 Quit
Beendet das Programm.

I.2 Start
Beginnt eine neue Messung.

I.3 Info
Informiert über das Programm, erläutert einige der Fragestellungen, die mit Hilfe des Programms bearbeitet werden können.

I.4 Autor Nennt den Autor des Programms.

I.5 Lizenz
Bringt die Adresse des Lizenznehmers auf den Bildschirm.

II MODUS II.1 Einzelbewegung zeigen
Ermöglicht die Bewegung eines einzelnen Planeten. Läßt gleichzeitig bis zu 10 Umläufe zu (wichtig bei nicht geschlossenen Planetenbahnen).

II.2 Alle Planeten zeigen
Zeigt die Bahnen der 5 erdnächsten Planeten und von 5 Planetoiden für jeweils 1 Umlauf.

II.3 Planeteninfo
Bringt Informationen über einen zu wählenden Planeten auf den Bildschirm.

II.4 Bilder zeigen
Bringt Fotos aus dem Planetensystem auf den Bildschirm. (Nicht in allen Versionen implementiert.)

III PARAMETER III.1 Energie und Flächen-Geschwindigkeit
Fragt nach Energie und Flächengeschwindigkeit des zu untersuchenden Planeten. Dabei werden nur relative Werte eingegeben, also Energie pro kg im Ver gleich zur Erde und Flächengeschwindigkeit im Vergleich zur Erde. Interessant, wenn die Bahnen gleicher Energie in Abhängigkeit von der Flächengeschwindigkeit (bzw. vom Drehimpuls) verglichen werden sollen, oder die Bahnen gleicher Flächenge schwindigkeit (Drehimpuls) in Abhängigkeit von der Energie.

III.2 Gravitations-Gesetz
Statt des r^-2 -Gesetzes kann ein modifiziertes Kraftgesetz verwendet werden mit dem Exponenten - 2+ß. ß wird abgefragt. Interessant für die Frage, ob bei anderen Kraftgesetzen auch geschlossene Bahnen möglich sind. Beim Planeten Merkur mit seiner relativistischen Massenabhängigkeit sind ähnliche Erscheinungen zu beobachten.

III.3 Planeten-Wahl
Definiert den zu untersuchenden Planeten durch Auswahl aus der Liste der existierenden Planeten.

III.4 Zeitschritt
Erfragt den Zeitschritt für die Simulation. Je größer die Exzentrizität e der Bahn, desto mehr Schritte pro Umlauf werden benötigt. Verändert man den Zeitschritt von Planet zu Planet, dann vermittelt die Dauer der Simulation einen falschen Eindruck von der Zeitdauer der Realbewegung. Obwohl fast kreisförmige Bahnen schon mit wenigen Zeitschritten ausreichend gut berechnet werden können, empfiehlt es sich doch, angepaßt an die Rechnergeschwindigkeit stets gleichgroße Zeitschritte zu verwenden. Es wird jedoch immer die Realzeit angezeigt und nur diese ist für die Ableitung der Kepler-Gesetze zu verwenden.

III.5 Mindestschrittzahl
Legt die kleinste zugelassene Schrittzahl fest. Das ist z.B. sinnvoll, wenn auch ein Eindruck vom Realzeit- Verlauf der Bewegung erhalten werden soll. Dann un terschreitet die Schrittzahl diesen Wert nicht, obwohl bei den nur schwach elliptischen Bahnen eine weitaus geringere Schrittzahl ausreichende Genauigkeit liefern würde.

IV AUSGABE IV.1 Fahrstrahl ein/aus
Schalter für den Fahrstrahl zur Ableitung des 2. Keplergesetzes. Arbeitet nicht zusammen mit IV.2.

IV.2 Planetenbild ein/aus
Zeichnet in 20 gleichen Zeitschritten auch die Position des Planeten als Kreisscheibe ein.

IV.3 Bildschirm löschen
Löscht den Bildschirm.
IV.4 Hardcopy
Gibt die Bildschirmgraphik auf einem EPSON-kompatiblen Drucker aus.

IV.5 Zeigen
Bringt den gewählten Graphen auf den Bildschirm; überschreibt frühere Meßkurven.

IV.6 Überschreiben ein/aus
Je nach Schalterstellung wird vor einer neuen Rechnung gelöscht oder nicht.

V FUNKTIONEN V.1 Halbachse messen
Ermöglicht es, die horizontale Achse bzw. Halbachse mit der Maus zu messen.

V.2 Flächen messen
Ermöglicht es, die Fläche zu messen, die der Fahrstrahl in einem festen Zeitintervall überstrichen hat. Funktioniert nur, wenn Fahrstrahl eingeschaltet ist. Es werden dann die Pixel ausgezählt, die beim Schwärzen der Fläche gesetzt werden müssen. Wegen der Ränder und der endlichen Bildschirmauflösung kann man keine übertriebene Meßgenauigkeit erwarten.

V.3 Exzentrizität messen
Ermöglicht es, mit der Maus die beiden Halbachsen zu messen und deren Verhältnis zu bilden.

V.4 Bahnparameter k messen
Mit der Maus wird der Bahnparameter k gemessen und angezeigt.

V.5 Sonnenposition definieren
Mit der Maus wird die Position der Sonne definiert.

VI DISK VI.1 Laden
Lädt eine Bildschirmgraphik aus einem frei wählbarem Verzeichnis. Es muß eine Graphik mit geeigneter Bildschirmauflösung gewählt werden. Die Bilddateien sind mit *.VGA, *.EGA, *.CG6, *.CG3 oder *.HRC gekennzeichnet.

VI.2 Speichern
Speichert eine Bildschirmgraphik in ein frei wählbares Verzeichnis.

ZUR THEORIE DER KEPLERBEWEGUNG: zurück

Die Kepler-Gesetze besagen:

1. Die Planeten bewegen sich auf Ellipsen um die Sonne; die Sonne steht im Brennpunkt der Ellipsen.

2. Der Fahrstrahl eines Planeten überstreicht in gleichen Zeiten gleiche Flächen.

3. Die Quadrate der Umlaufszeiten verschiedener Planeten verhalten sich wie die dritten Potenzen der Halbachsen.

Definition der Bahnparameter bei der Kepler-Ellipse

Die konstante Flächengeschwindigkeit A garantiert, daß der Drehimpuls L konstant ist und daß eine Zentralkraft vorliegt.

Das 1. Kepler-Gesetz zusammen mit dem dritten garantiert, daß die wirkende Kraft proportional zu r^-2 vom Sonnenabstand abhängt.

Das 3. Kepler-Gesetz legt zusätzlich noch fest, daß die Proportionalitätskonstante im Kraftgesetz, abgesehen von der Masse des Planeten, unabhängig vom einzelnen Planeten ist (Gravitationsgesetz: F_G = - G m r^-2 ; G = G . M_S).

Es gelten folgende Beziehungen:

(1) F_G = - G m r^-2 (Kraft)

(2) L = m r² f* = m.2.A = m Ö (k G) (Drehimpuls L ; Begründung unten)

(3) E = - Gm/(2a) (Energie E; große Halbachse a ; Begründung unten)

(4) G = G . M_S = 1,33.10²⁰ m³/s² mit der Gravitationskonstanten G und der Sonnenmasse M_S. Das könnte man als spezifische Gravitationskonstante für das Sonnensystem bezeichnen.

Messung des Bahnparameters k

Kepler-Gesetze und Planetenbewegung

(5) Bahngleichungen:

a) in kartesischen Koordinaten:

(5a) (x/a)²+(y/b)² = 1

mit der großen Halbachse a und der kleinen Halbachse b

b) in Polarkoordinaten:

(5b) 1/r = 1/k (1 + e cos f )

mit der numerischen Exzentrizität e und dem Bahnparameter k mit (aus 5):

(6) k = b²/a

Für f = 90° folgt aus (5b) r = k. Darauf beruht die Messung von k im Programm. Es gibt folgende weitere Beziehungen:

(7) k = a (1 - e ²) e ²= 1 - k/a = 1 - (b/a)²

e aus der Gleichung e²= a² - b² heißt lineare Exzentrizität. Es gilt

(7') e = e/a

(8) Der Brennpunktsabstand ist 2 a e . Darauf beruht die Messung der numerischen Exzentrizität e im Programm.

(9) Wegen A²= 1/4 . (L/m)²= 1/4 . k G mit G aus dem Kraftgesetz und der Planetenmasse m bestimmt die Flächengeschwindigkeit A bzw. der Drehimpuls L pro Masseneinheit ("spezifischer Drehimpuls") den Bahnparameter k bzw. das Achsenverhältnis (die Abplattung).

(10) Wegen E /m = -G/(2a) bestimmt die Energie (pro Masseneinheit) die große Halbachse a.

Bahnen gleicher Energie (pro Masseneinheit) haben deshalb die gleiche große Halbachse (und Umlaufszeit).
Bahnen gleichen Drehimpulses (pro Masseneinheit) haben deshalb die gleiche Abplattung k und schneiden sich im selben, durch k festgelegten Punkt.

(11) Vergleicht man mit den Erddaten:

E_E /m_E = -G/(2a_E) und A_E²= 1/4 . (L_E/m_E)²= 1/4 . G. k_E

so erhält man:

( E / m ) / ( E_E/ m_E ) = a / a_E

und

A² / A_E²= (L/m)² / (L_E/m_E)² = k / k_E

Die Energien pro Masseneinheit verhalten sich deshalb wie die großen Halbachsen, die Quadrate der Flächengeschwindigkeit bzw. der Drehimpulse pro Masseneinheit wie die Bahnparameter k.

Energie zurück

Für die Gesamtenergie gilt:

(12) E = m/2 ( r*² + r²w²) - Gm/r andererseits: (r* = dr/dt: Radialgeschwindigkeit)

(13) L = m r².w , also w = L/mr² und damit

(12') E = m/2 ( r*² + L² /m²r² ) - Gm/r = m/2 r*² + ( L²/2mr² - Gm/r)

L²/2mr² - Gm/r wird üblicherweise zu einem effektiven Potenzial zusammengefasst, wobei ein Anteil das so genannte Zentrifugalpotenzial ist. Die Graphik zeigt schematisch das effektive Potenzial:

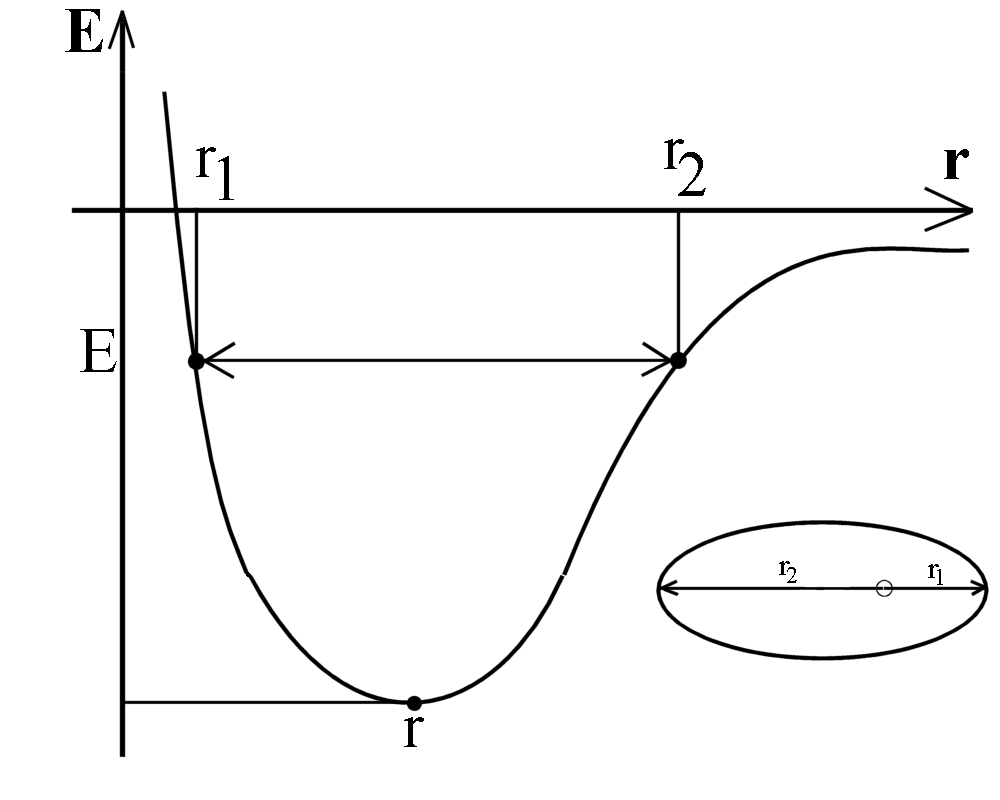Falls dr/dt = r* = 0 (Umkehrpunkte), gilt E = L²/2mr² - Gm/r . Das passiert offenbar bei zwei Radien r₁ und r₂. Es gilt nach Multiplikation mit r²:
E.r² + Gm.r - L²/2m = 0
Die quadratische Gleichung für r hat 2 Lösungen, r₁und r₂, und es gilt:
r₁= 1/2E ( - Gm + Ö G²m² + 2EL²/m ) und
r₂= 1/2E ( - Gm - Ö G²m² + 2EL²/m )
Für die Summe beider: r₁+r₂ = 2a =>
2a = - Gm/E, also

E = - Gm/2a

Die Gesamtenergie pro Masseneinheit ("spezifische Gesamtenergie") hängt nur von der großen Halbachse ab. Diese wiederum bestimmt nach dem 3. Kepler-Gesetz die Umlaufszeit.

Effektives Potenzial aus Gravitationspotenzial und
"Zentrifugalpotenzial": Abhängigkeit vom Radius.
An den "Umkehrpunkten" (bei den Radien r₁und r₂) ist die Radialgeschwindigkeit 0. Dazu passen die
entsprechenden Positionen auf der Kepler-Ellipse.

Drehimpuls zurück

Für die Ellipsenfläche F gilt: F = a.b.p. Damit wird die Flächengeschwindigkeit

A = F/T = a.b.p/T Also bei gleicher Energie ( => gleiche große Halbachse a, => gleiche Umlaufszeit T):

A₁/A₂ = b₁/b₂.T₂/T₁ = b₂/b₁

(A₁/A₂)² = (b₁/b₂)² = (b₁/b₂)² (a₂/a₁) = k₁/k₂

Andererseits:

1/T² = G/4p²1/a³

(L/m)² =4A² = 4a²b²p²/T² = 4a²b²p²G/4p²a³ = b²/a G = k G

Der "spezifische Drehimpuls" L/m bestimmt damit den Bahnparameter k.

MENÜPUNKTE	zurück
I DESK	I.1 Quit Beendet das Programm. I.2 Start Beginnt eine neue Messung. I.3 Info Informiert über das Programm, erläutert einige der Fragestellungen, die mit Hilfe des Programms bearbeitet werden können. I.4 Autor Nennt den Autor des Programms. I.5 Lizenz Bringt die Adresse des Lizenznehmers auf den Bildschirm.
II MODUS	II.1 Einzelbewegung zeigen Ermöglicht die Bewegung eines einzelnen Planeten. Läßt gleichzeitig bis zu 10 Umläufe zu (wichtig bei nicht geschlossenen Planetenbahnen). II.2 Alle Planeten zeigen Zeigt die Bahnen der 5 erdnächsten Planeten und von 5 Planetoiden für jeweils 1 Umlauf. II.3 Planeteninfo Bringt Informationen über einen zu wählenden Planeten auf den Bildschirm. II.4 Bilder zeigen Bringt Fotos aus dem Planetensystem auf den Bildschirm. (Nicht in allen Versionen implementiert.)
III PARAMETER	III.1 Energie und Flächen-Geschwindigkeit Fragt nach Energie und Flächengeschwindigkeit des zu untersuchenden Planeten. Dabei werden nur relative Werte eingegeben, also Energie pro kg im Ver gleich zur Erde und Flächengeschwindigkeit im Vergleich zur Erde. Interessant, wenn die Bahnen gleicher Energie in Abhängigkeit von der Flächengeschwindigkeit (bzw. vom Drehimpuls) verglichen werden sollen, oder die Bahnen gleicher Flächenge schwindigkeit (Drehimpuls) in Abhängigkeit von der Energie. III.2 Gravitations-Gesetz Statt des r^-2 -Gesetzes kann ein modifiziertes Kraftgesetz verwendet werden mit dem Exponenten - 2+ß. ß wird abgefragt. Interessant für die Frage, ob bei anderen Kraftgesetzen auch geschlossene Bahnen möglich sind. Beim Planeten Merkur mit seiner relativistischen Massenabhängigkeit sind ähnliche Erscheinungen zu beobachten. III.3 Planeten-Wahl Definiert den zu untersuchenden Planeten durch Auswahl aus der Liste der existierenden Planeten. III.4 Zeitschritt Erfragt den Zeitschritt für die Simulation. Je größer die Exzentrizität e der Bahn, desto mehr Schritte pro Umlauf werden benötigt. Verändert man den Zeitschritt von Planet zu Planet, dann vermittelt die Dauer der Simulation einen falschen Eindruck von der Zeitdauer der Realbewegung. Obwohl fast kreisförmige Bahnen schon mit wenigen Zeitschritten ausreichend gut berechnet werden können, empfiehlt es sich doch, angepaßt an die Rechnergeschwindigkeit stets gleichgroße Zeitschritte zu verwenden. Es wird jedoch immer die Realzeit angezeigt und nur diese ist für die Ableitung der Kepler-Gesetze zu verwenden. III.5 Mindestschrittzahl Legt die kleinste zugelassene Schrittzahl fest. Das ist z.B. sinnvoll, wenn auch ein Eindruck vom Realzeit- Verlauf der Bewegung erhalten werden soll. Dann un terschreitet die Schrittzahl diesen Wert nicht, obwohl bei den nur schwach elliptischen Bahnen eine weitaus geringere Schrittzahl ausreichende Genauigkeit liefern würde.
IV AUSGABE	IV.1 Fahrstrahl ein/aus Schalter für den Fahrstrahl zur Ableitung des 2. Keplergesetzes. Arbeitet nicht zusammen mit IV.2. IV.2 Planetenbild ein/aus Zeichnet in 20 gleichen Zeitschritten auch die Position des Planeten als Kreisscheibe ein. IV.3 Bildschirm löschen Löscht den Bildschirm. IV.4 Hardcopy Gibt die Bildschirmgraphik auf einem EPSON-kompatiblen Drucker aus. IV.5 Zeigen Bringt den gewählten Graphen auf den Bildschirm; überschreibt frühere Meßkurven. IV.6 Überschreiben ein/aus Je nach Schalterstellung wird vor einer neuen Rechnung gelöscht oder nicht.
V FUNKTIONEN	V.1 Halbachse messen Ermöglicht es, die horizontale Achse bzw. Halbachse mit der Maus zu messen. V.2 Flächen messen Ermöglicht es, die Fläche zu messen, die der Fahrstrahl in einem festen Zeitintervall überstrichen hat. Funktioniert nur, wenn Fahrstrahl eingeschaltet ist. Es werden dann die Pixel ausgezählt, die beim Schwärzen der Fläche gesetzt werden müssen. Wegen der Ränder und der endlichen Bildschirmauflösung kann man keine übertriebene Meßgenauigkeit erwarten. V.3 Exzentrizität messen Ermöglicht es, mit der Maus die beiden Halbachsen zu messen und deren Verhältnis zu bilden. V.4 Bahnparameter k messen Mit der Maus wird der Bahnparameter k gemessen und angezeigt. V.5 Sonnenposition definieren Mit der Maus wird die Position der Sonne definiert.
VI DISK	VI.1 Laden Lädt eine Bildschirmgraphik aus einem frei wählbarem Verzeichnis. Es muß eine Graphik mit geeigneter Bildschirmauflösung gewählt werden. Die Bilddateien sind mit .VGA, .EGA, .CG6, .CG3 oder .HRC gekennzeichnet. VI.2 Speichern* Speichert eine Bildschirmgraphik in ein frei wählbares Verzeichnis.