Es handelt sich um kein Paradoxon.
|
| . |
|
Induktion ohne Magnetfeld? |
| . |
| Es geht hier um einige Sonderfälle der Induktion, die bei naiver Argumentation zu Verständnisschwierigkeiten führen. |
Natürlich darf am Induktionsgesetz nicht gerüttelt werden:
|
Längs einer geschlossenen Kurve C entsteht eine (elektrische)
Ringspannung (Umlaufspannung), wenn sich innerhalb von C der
magnetische Fluss Φ ändert.
|
Es soll auch nicht daran gerüttelt werden, dass es verschiedene Möglichkeiten gibt, den magnetischen Fluss zu ändern, z.B. durch ein zeitabhängiges Magnetfeld bzw. durch die Bewegung der Kurve C durch ein inhomogenes Magnetfeld oder durch eine Änderung der von der Kurve C umfassten Fläche.
Allerdings wird man in Schulbüchern oder auch esoterischen Schriften immer wieder auf Situationen gestoßen, bei denen scheinbar an solchen Orten, wo die Induktion angeblich stattfinden soll, weit und breit kein Magnetfeld zu finden ist. Der Grund ist einfach, dass Induktion in gewisser Weise ein nichtlokaler Effekt ist. Das soll im Folgenden an Beispielen erläutert werden. Die Erläuterung soll zu einem tieferen und zugleich einfacheren Verständnis der elektromagnetischen Induktion führen. Es geht also um:
1. den Maxwell-Lodge-Effekt
2. die fälschlich so genannte "Induktion im bewegten Leiter", für den Fall, dass der "bewegte Leiter" gegen ein Magnetfeld vollständig abgeschirmt ist [3],
3. den so genannten "Hooper-Monstein-Effekt", wenn durch Überlagerung von Magnetfeldern dafür gesorgt wird, dass am Ort des Leiters immer das Magnetfeld 0 herrscht.
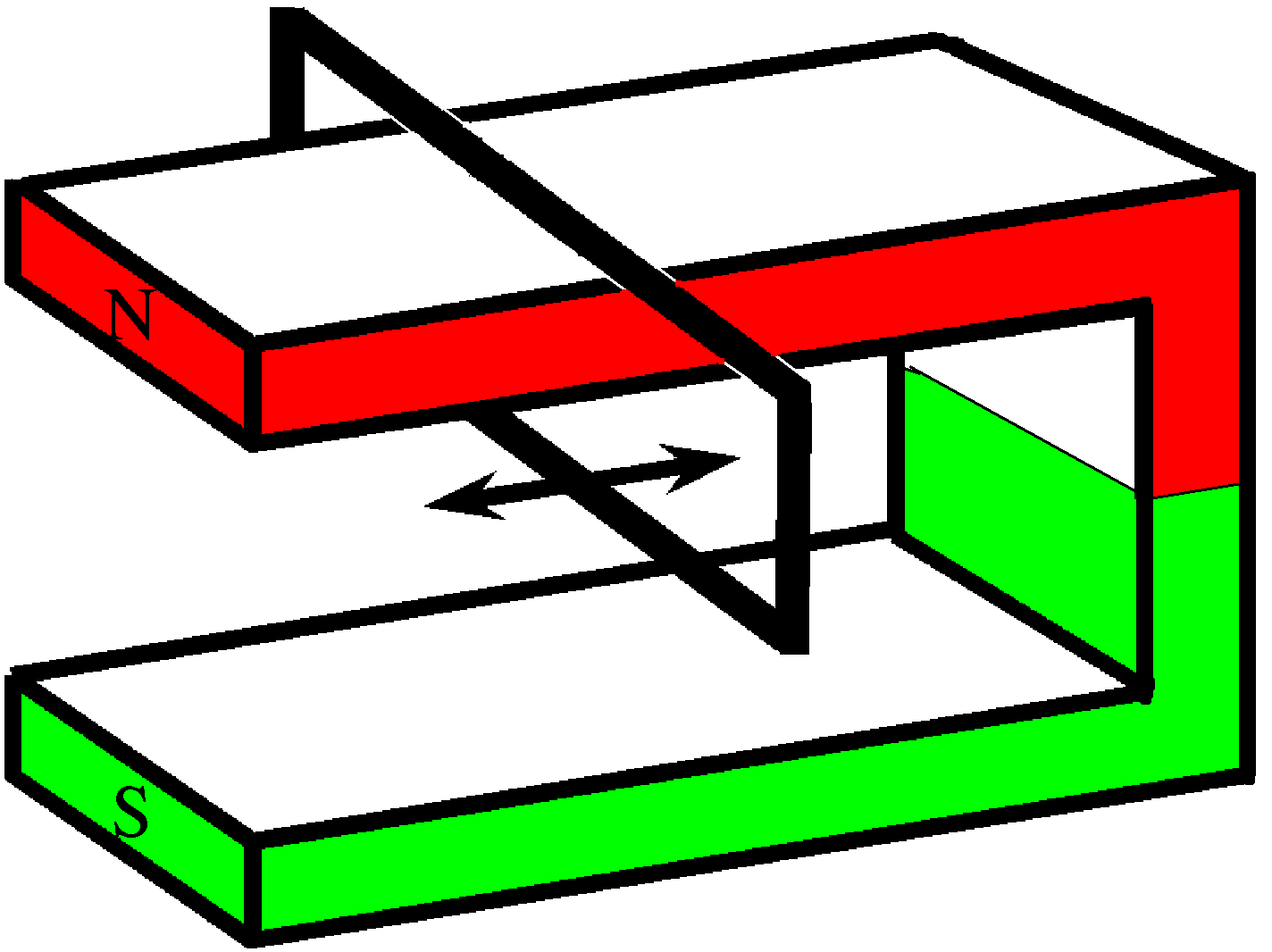
4. das "Hufeisen-Paradoxon", bei dem ein Leiterring um einen Schenkel des Hufeisenmagneten hin und her bewegt wird.
| . |
Es soll noch erwähnt werden, dass man auch in einem anderen Fall keinerlei Leiter oder Ladungen für die Entstehung der Induktion benötigt: bei der Ausbreitung der elektromagnetischen Wellen.
Dabei erzeugt man durch eine langgestreckte Zylinder-Spule mit dem Radius R ein weitgehend auf den Innenraum der Spule beschränktes zeitabhängiges Magnetfeld, das durch einen Eisenkern sogar noch verstärkt werden kann. Koaxial zur Spulenachse wird eine Induktionsschleife mit Radius r gelegt. Sie befindet sich ganz in einem Bereich, in dem das Magnetfeld vernachlässigbar ist. Kein Teil der Induktionsschleife "bemerkt" also etwas vom sich zeitlich verändernden Magnetfeld. Dennoch wird eine Induktionsspannung nach dem üblichen Induktionsgesetz gemessen, weil sich im Inneren der Induktionsschleife, beschränkt auf das Innere der Feldspule, der magnetische Fluss ändert. Die Messung zeigt auch, dass diese Induktionsspannung unabhängig vom Radius r der Induktionsschleife ist. Moderne Forschungsarbeiten bestätigen das. Nach der Theorie ist alles klar:
1. Uind = - n. dΦ/dt , wobei n = 1 und Φ = B(t).F mit der Querschnittsfläche F = R2.π der Feldspule. Man sieht, wie eine zeitliche Stromänderung über die Ableitung von B(t) zur Induktionsspannung führt. Nur jemand, der glaubt, dass Induktion durch das lokale Magnetfeld am Ort der Induktionsschleife zustandekommt, wundert sich über das Ergebnis.
2. Wenn man das Induktionsgesetz mit Hilfe des Vektorpotenzials A formuliert (siehe Elektrodynamisches Märchen), lautet das Induktionsgesetz für diesen Fall also E = - ∂A/∂t ( ∂ soll die partielle Ableitung kennzeichnen). Damit würden Lokalitäts-Gläubige zufrieden gestellt werden: In dieser Formulierung der Elektrodynamik hängt das elektrische Feld E von der zeitlichen Änderung des Vektorpotenzials A am gleichen Ort ab. Und genaueres Nachrechnen mit dem rein azimutalen A = Aφeφ , wobei Aφ = ½ B R2 1/r würde auch hier zeigen, dass Uind = ∫ 0 E·ds = - d/dt ∫ 0 A·ds = - d/dt ( 2.r.π. ½ B R2 1/r ) = - d/dt ( R2π B ) = - dΦ/dt ist, also unabhängig vom Radius r der Induktionsschleife.
An diesem Effekt ist nichts Besonderes. Er ist eine direkte Folge des Induktionsgesetzes in der Form der "Flussregel".
| . |
So wird in Schulbüchern üblicherweise der Fall der Induktion bezeichnet, bei dem ein Teil der Leiterschleife (eine Leiterbrücke) sich durch ein Magnetfeld bewegt. Es ist klar, dass eine solche Bezeichnungsweise nur in einem bestimmten Bezugssystem einen Sinn hat, nämlich in dem, in dem das Magnetfeld gemessen wird, relativ zu dem sich die Leiterbrücke bewegt. Sie bewegt sich also auch relativ zu dem Bezugssystem, in dem der Rest der Leiterschleife und das Messgerät ruht. Die Problematik der Bezeichnungsweise ergibt sich aus der Tatsache, dass in Wirklichkeit jeder Leiter zugleich bewegt ist und zugleich ruht, je nach Bezugssystem.
Für die Herleitung der Induktionsspannung in diesem Fall wird üblicherweise die Lorentz-Kraft verwendet (*). Auch die Ringspannung ist Arbeit W (für einen Umlauf) pro transportierter Ladungsmenge: Uind = W/(-e) , wobei W die Arbeit für einen vollen Umlauf für ein Elektron ist. Zum Umlaufsintegral der Ringspannung Uind = ∫0 F·ds (∫ 0 kennzeichnet das Umlaufsintegral über einen geschlossenen Weg C längs der Leiterschleife) kann nur der Anteil innerhalb der Leiterbrücke beitragen, weil in ihm allein eine Kraft F wirkt und eine Arbeit bei der Verschiebung von Ladungen verrichten kann, eben die Lorentz-Kraft. Also gilt :
Uind = B.v.l
Mit anderen Überlegungen wird gezeigt, dass dies die Flussänderung als Folge der Flächenänderung des von Leiterschleife inkl. Leiterbrücke eingeschlossenen magnetischen Flusses ist.
Für die Herleitung hier wurde bewusst ein anderer Weg gewählt als in den meisten Schulbüchern. Dort wird ohne Kommentar noch ein Schritt zwischengeschaltet, nämlich die Messung der Lorentz-Kraft. Dazu bewegt man die Leiterbrücke zunächst in gleicher Weise, aber als isolierten Leiterstab, durch das Magnetfeld. Es bildet sich dann ein elektrostatisches E-Feld und eine zugehörige elektrische Kraft aus, die bei Kräftegleichgewicht im Inneren des Stabs von gleichem Betrag wie die Lorentz-Kraft ist. Mit dieser Kenntnis wird dann eine elektrostatische Spannung berechnet, im Prinzip wieder als Arbeit pro Ladung. Weshalb diese elektrostatische Spannung von gleichem Betrag wie die Ringspannung ist, die eigentlich gesucht wird, die einen Induktionsstrom durch die Leiterschleife C fließen lässt, wird in der Schule meist weggelassen. (Die elektrostatische Spannung kann sich nur im isolierten Leiterstab ausbilden.) Es wird meist gesagt, dass diese (elektrostatische) Spannung "zwischen den Enden des Stabs gemessen wird".
Wie oben gezeigt (*) könnte man in der Schule argumentieren. Aber was geschieht, wenn man die Leiterbrücke magnetisch abschirmt [3] , so dass am Ort der Brücke garantiert kein magnetisches Feld herrscht? Gibt es dann keine Lorentz-Kraft? Dann gäbe es nach obiger Argumentation auch keine Induktionsspannung. Ein Versuch zeigt aber, dass die Abschirmung keinen Einfluss hat.
Dazu verwendet man ein "formiertes" Röhrchen aus Mue-Metall, durch das die Windung(en) der Induktionsspule laufen. Mit der Hall-Sonde wird nachgemessen, dass im homogenen Feldbereich eines Hufeisenmagneten das Röhrchen-Innere feldfrei ist. Der Hufeisenmagnet wird so platziert, dass die anderen 3 Seiten der Induktionsspule in Bereichen mit vernachlässigbarem Magnetfeld liegen. Also erfahren auch die durchlaufenden Windungen kein magnetisches Feld.
Setzt man sich in das Bezugssystem des Leiterbügels, wird überall ein elektrisches Feld E = v x B beobachtet, wo /B/ von 0 verschieden ist. Es handelt sich eine Bewegung relativ zu einem Bezugssystem, in dem B gemessen wurde. In diesem BZS argumentierend kann an den Elektronen Arbeit durch eine elektrische Kraft als Folge von E verrichtet werden. Auch diese Argumentation führt im Fall des vollständig abgeschirmten Magnetfelds zu einer verschwindenden Arbeit. Also wieder: Induktion muss auch hier ein nichtlokaler Effekt sein. Der von der Leiterschleife eingeschlossene magnetische Fluss ändert sich auf jeden Fall!
Etwas allgemeiner ist die Erklärung eigentlich noch einfacher: Das Induktionsgesetz, wie es auch eingangs formuliert wurde, ist unabhängig davon, ob die Kurve C mit Leitern belegt ist oder nicht, oder ob lokal gar kein Magnetfeld vorhanden ist. Das zeigt die Herleitung des Gesetzes, wie sie in vielen Elektrodynamik-Lehrbüchern zu finden ist, und z.B. auch in einem anderen Text von mir dargelegt wurde. Im Wikipedia-Artikel zur elektromagnetischen Induktion, dem ich wirklich nicht in allen Punkten zustimmen kann, wird auf den Unterschied zwischen der Bewegung einer mathematischen Kurve C mit der Geschwindigkeit u und der eines Leiters mit der Geschwindigkeit v hingewiesen. Dort würde wohl zur Erklärung des scheinbaren Paradoxons eine Integralform II des Induktionsgesetzes herangezogen, in der die Geschwindigkeit u auftaucht, nicht v. u und v stimmen natürlich überein, wenn C mit Leitern belegt ist. Dann eben bringt man mit Recht die Lorentz-Kraft ins Spiel.
| . |
Es handelt sich eigentlich um eine Variante des vorherigen Versuchs. Auch hier wird ein Leiter betrachtet (als Teil einer geschlossenen Leiterschleife), "zwischen dessen Enden die Induktionsspannung gemessen wird". Durch zwei entgegengesetzt gepolte Permanentmagnete wird dafür gesorgt, dass das Magnetfeld an der Stelle des Leiters verschwindet. Etwas raffinierter wird die Anordnung noch dadurch gemacht, dass die beiden Magnete synchron bewegt werden, so dass sich Bedingung B = 0 am Ort des Leiters bei beliebigem Abstand der Magnete vom Leiter einstellt.Wenn nur mit der Lorentz-Kraft argumentiert wird, sieht es oberflächlich so aus, als könne es hier nicht zur Induktion kommen. Die Messung und die Theorie zeigen das Gegenteil. Tatsächlich bilden die Zuführungen zum Leiter mit dem Messgerät wieder eine Induktionsschleife, in der sich der magnetische Fluss ändert, diesmal durch die Bewegung der beiden Magnete. Nichts Besonderes, alles im Einklang mit dem Induktionsgesetz; kein Anlass, die traditionelle Elektrodynamik in Frage zu stellen!
| . |
 |
Über den Schenkel eines Hufeisenmagneten wird ein recheckiger Leiterring gestülpt und hin und her bewegt. Man ist geneigt, unterschiedlich zu argumentieren. Einerseits "bemerkt" kein Teil des Rings allein unter Beachtung des Magnetfelds eine Bewegung: Die Rechtecksseite des Rings zwischen den Schenkeln "bemerkt" immer nur das gleiche homogene Magnetfeld; woher sollten die Elektronen im Ring wohl "wissen", dass sie sich im Magnetfeld bewegen? [Nur im ja wohl inkorrekten "Stachelmodell" des Magnetfeld wäre das klar: die Elektronen würden immer wieder an anderen Magnetfeld-Stacheln vorbeikommen.] Die drei Rechtecksseiten außerhalb des Zwischenbereichs befinden sich in guter Näherung immer in einem Bereich ohne Magnetfeld. Also keine Induktion!? Andererseits, formal argumentierend, müsste für den Zwischenbereich mit dem quasi homogenen B-Feld die Lorentz-Kraft anwendbar sein. Sie würde zur Induktion führen. Noch einmal anders: der Ring verbleibt, so scheint es, immer in einer Ebene parallel zu den Magnetfeldlinien (von N nach S), es findet scheinbar weder eine Flächenänderung noch eine Magnetfeldänderung statt; der magnetische Fluss scheint ungeändert = 0. Danach dürfte es wieder nicht zur Induktion kommen. Das sieht nach einem Paradoxon aus. |
 |
Tatsächlich ist klar: Die Lorentz-Kraft führt zur Induktion
und es findet auch eine Änderung des magnetischen Flusses F
statt, ähnlich wie beim Maxwell-Lodge-Experiment. Auch
hier ändert sich F nur
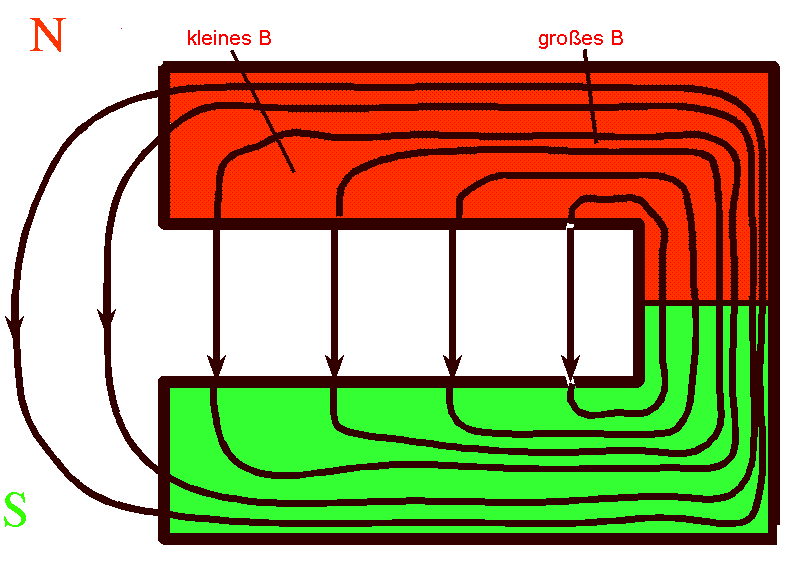
weit im Inneren des Rings, nämlich im Schenkel, dort, wo die
B-Feldlinien im Schenkel die Ringfläche durchstoßen, nicht in
der Nähe des Leiters. Im Schenkel ist die magnetische
Flussdichte B parallel zum Schenkel, senkrecht zur
Ringfläche, je nach Position des Rings größer oder kleiner (nahe
des Magnetpols). Beide Argumente bestätigen das Experiment. Die
Elektronen bemerken auch keine Kraft, die lokal bei ihnen
entsteht ("gemacht wird"); die Stacheln sind überflüssig,
sondern "alle Felder überall wirken so zusammen, als würde an
ihrem Ort eine solche Lorentz-Kraft entstehen". Eine magnetische
Abschirmung könnte auch in diesem Fall die Induktion nicht
unterdrücken. Induktion ist, mit dem B-Feld formuliert,
nichtlokal.
Es handelt sich um kein Paradoxon. |
Auf jeden Fall geht die Induktion vom Strom im Leiter aus und macht sich anderswo durch die Ringspannung bemerkbar. Wie diese Wirkung vom Ort des Stroms zur Induktionsschleife kommt, kann mit dieser Betrachtungsweise ohne die Berücksichtigung der Ausbreitung von E- oder B-Feldern in Raum und Zeit nicht beschrieben oder untersucht werden. Es ist eine (i.A. gute) Näherung, dass eine Stromänderung in der Feldspule instantan zu Änderungen der Felder führt. Vermutlich hat dies nie jemand genauer untersucht, und möglicherweise liegt eine damit zusammenhängende kausale Betrachtung ohnehin außerhalb des Rahmens der konsistenten Betrachtungsweise der Maxwell-Gleichungen. Sie beschreiben m.E., wie Ströme und Ladungen mit Feldern zusammenhängen, nicht, wie solche entstehen.
| . |
Literatur:
Was ist elektromagnetische Induktion ?
[1] Maxwell-Lodge statt Aharonov-Bohm, http://www.pro-physik.de/Phy/leadArticle.do?laid=10910, 2008
[2] Zum esoterischen "Hooper-Monstein-Effekt": z.B. www.rqm.ch/Reflexionen Hilscher.htm, http://jnaudin.free.fr/html/hoopmnst.htm , und seine Klarstellung:
http://www.forphys.de/Website/induktion/induktion.html
[3] U. Manthel, P. Täubert, Zur Induktionsspannung, Eine kritische Betrachtung, PdN-Ph, Heft 6, 1986, S. 24 - 27