Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig-keiten im Physik-UR Anschau-liche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Phys. Analysen Im- pres- sum Kommen-tare und Wünsche © Horst Hübel Würzburg 2005 - 2018

Schon lange werden in der Physik-Didaktik Verfahren diskutiert, die ein Verständnis des einfachen Gleichstromkreises und des Spannungsbegriffs für Schüler erleichtern sollen.

Beim Gleichstromkreis mit einem stationären Strom gibt es jedoch einige objektive Schwierigkeiten:

1. Während bei der Entladung eines Kondensators das elektrische Potenzialfeld Ursache für die Bewegung der Elektronen ist, findet man in Lehrbüchern der Elektrodynamik einen Beweis, dass ein reines Potenzialfeld nicht die Energie für einen stationären Strom heranführen kann (weil ständig Stromwärme abgegeben wird). Anhänger der Potenzialvorstellung müssten also erklären, woher die Energie kommt.

Per definitionem wird bei einem Potenzialfeld jedem Punkt des Raumes ein eindeutiges Potenzial zugeordnet, das - abgesehen von einer additiven Konstanten im Zusammenhang mit dem Potenzialnullpunkt - ausschließlich von dem an diesem Punkt vorhandenen Feld abhängt. In der Elektrodynamik ist ein Potenzialfeld an die "Wegunabhängigkeit der (Verschiebungs-)Arbeit" bei einer Verschiebung einer Ladung von einem Potenzialnullpunkt zum betrachteten Punkt gebunden. Ganz gleich, auf welchem Weg die Verschiebung erfolgt, die Verschiebungsarbeit ist zum betrachteten Punkt immer gleich. Das hängt damit zusammen, dass das elektrische Feld in diesem Fall "wirbelfrei" ist (formal: rot E = 0).

2. Die chemischen Vorgänge in der Batterie, die die Ursache für den Stromfluss sind, liegen außerhalb der Elektrodynamik.

Es sind deshalb drei Strategien üblich zur Behandlung der Probleme:

1. Das Problem wird ignoriert. Es wird die Existenz eines Potenzialfelds uneingeschränkt behauptet. Der Gleichstromkreis mit dem stationären Strom wird behandelt wie die Entladung eines Kondensators. Abgesehen von Fragen, die mit der Batterie, der Energiebeschaffung und der Ursache des Stroms zusammenhängen, ergeben sich offenbar für die Praxis kaum Abweichungen. Der Standpunkt wird häufig auch eingenommen, wenn Oberflächenladungen auf den Leitern untersucht werden, die dafür sorgen, dass in den Leitern das elektrische Feld der Leitergeometrie folgt. Natürlich können auch Oberflächenladungen nicht die Energie für den stationären Strom liefern.

2. Die chemischen Vorgänge in der Batterie werden simuliert durch ein "eingeprägtes elektrisches Feld", lokalisiert in der Batterie. Dann kann ganz innerhalb der Elektrodynamik argumentiert werden. Das Gesamtfeld E, zusammengesetzt aus eingeprägtem Feld und "echtem" elektrischen Feld, ist dann nicht wirbelfrei, also kein Potenzialfeld; die Wegunabhängigkeit fehlt für E, wie es physikalisch auch sein muss. Ein stationärer Strom wird damit zugelassen, verursacht durch das "eingeprägte elektrische Feld". Die Vorgehensweise ähnelt den Verhältnissen bei der elektromagnetischen Induktion, bei der  - wenigstens in bestimmten Bezugssystemen - ein elektrisches Wirbelfeld typisch ist.

3. Es gibt Lehrbücher, die zwischen beiden Batteriepolen einen Potenzialsprung innerhalb der Batterie einführen, um nicht über "eingeprägte Kräfte" reden zu müssen. Das rettet formal den physikalischen Sachverhalt bzgl. der beiden Probleme, entspricht aber nicht dem üblicherweise stetigen Potenzial, verletzt die Wegunabhängigkeit des Potenzial und erklärt nichts.

Betrachten wir jetzt die Vorgehensweise nach der ersten Strategie. Unter anderem wird behauptet, dass dabei wie bei der Entladung eines Kondensators ein Potenzial eine Rolle spiele. Physik-Lehrer werden von Vertretern der Didaktik aufgefordert, dieses Potenzial zu vermitteln und die Spannung allgemein als Potenzialdifferenz zu definieren. Letzteres ist in der Elektrostatik zweifellos richtig, weil dort ein Potenzial existiert. Per Definitionen ist aber ein Potenzial an die Wegunabhängigkeit der Arbeit bei der Verschiebung einer elektrischen Ladung gebunden. Sie gilt nicht für den Gleichstromkreis.

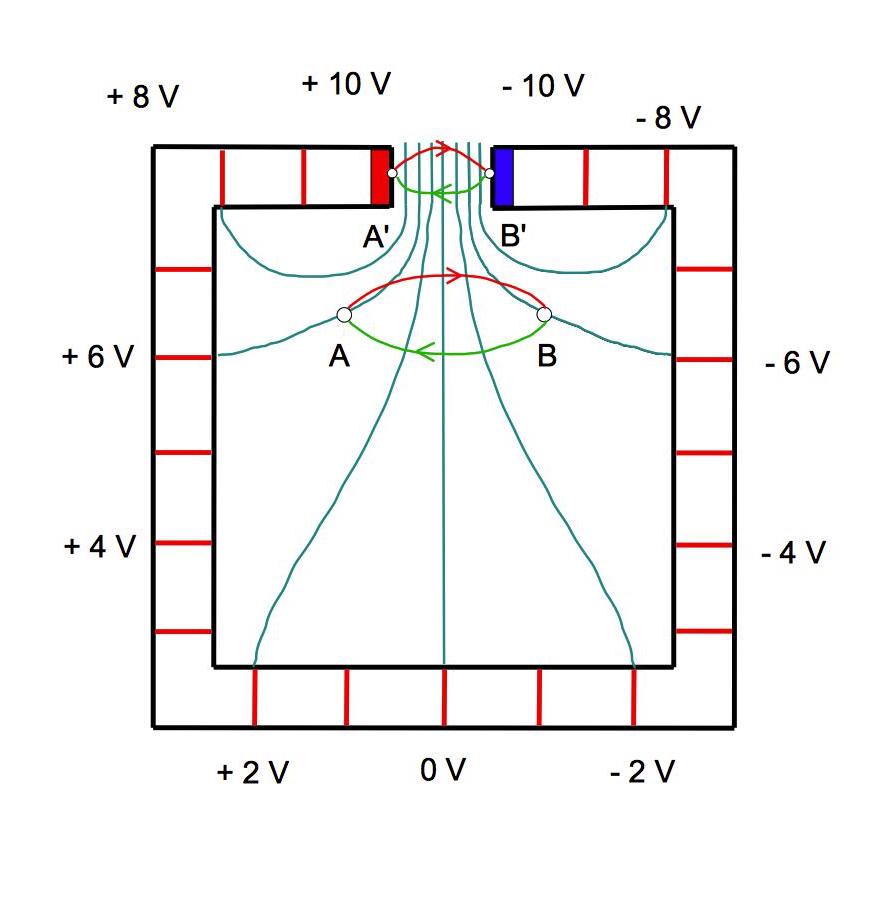
Strategie 1 soll erläutert werden anhand einer Zeichnung, die ich einer didaktischen Veröffentlichung nachempfunden habe, die eine qualitative Konstruktion von "Äquipotenziallinien" und damit verbundenen Oberflächenladungen propagiert. Sie soll zu einem homogenen Gleichstromkreis mit einer Batterie (20 V) gehören. Ich habe die eingezeichneten Spannungswerte durch "Äquipotenziallinien" (türkis) verbunden, die der Autor der Veröffentlichung vielleicht genauer eingezeichnet hätte, aber das spielt für diese Diskussion keine Rolle. Betrachten Sie die Punkte A und B. Schauen wir uns erst die Kräfte auf ein freies Elektron an: F ist längs eines Gradienten des Potenzials gerichtet, also tendenziell von B nach A. (1) Von B nach A (angeblich auf einem beliebigen Weg) bewegt sich ein freies Elektron, an die Stelle B gebracht,  "von allein" (durch das elektrische Feld) z.B. nach A (grüner Weg): das Elektron verliert dabei 12 eV Energie, die im Prinzip mit irgendwelchen Mechanismen abgefangen werden könnte. Um das Elektron von A nach B (angeblich wieder auf einem beliebigen Weg; rot) zurück zu bewegen, muss von außen Arbeit aufgewendet werden, und zwar mindestens 12 eV. Insgesamt ist alle abgegebene Arbeit wieder zurück gewonnen, wenn das Elektron wieder bei B ruht. Wenn das Elektron noch beschleunigt werden soll, werden mehr als 12 eV benötigt. Ein geeigneter Mechanismus soll auch die Entstehung von kinetischer Energie verhindern. In einem Kondensatorfeld wäre das zweifellos richtig.

(2) Das gleiche gälte für zwei Punkte A' und B' auf den Elektroden der Batterie. Die elektrische Feldkraft ist bei Vorliegen eines Potenzials vom Minuspol weg gerichtet, in der Zeichnung sowohl nach links als auch nach rechts. Wenn sich das Elektron anfänglich bei B' befindet, hat es 10 eV Energie. Bewegt es sich jetzt weiter - anfänglich nach rechts - durch den Stromkreis nach A' (grün), gibt es 20 eV ab, z.B. als Stromwärme. Es verbleibt die Energie -10 eV. Jetzt müsste Arbeit von außen gegen das elektrische Feld in der Batterie verrichtet werden um das Elektronen gegen die elektrische Abstoßung zum Minuspol B' zu befördern (rot). Dabei nähme das Elektron auf dem Weg von A' nach B' 20 eV wieder auf und hätte dann wieder 10 eV.  

(3) Aber so ist es nicht. Es sind die "eingeprägten Kräfte", die das Elektron von A' nach B' ohne zusätzliche äußere Kraft zurück befördern. Sie bringen die 20 eV auf. Auf dem vollen Weg B'-A'-B' hat das Elektron insgesamt keine Energie abgegeben und aufgenommen. Das elektrische Feld ist (quasi) unverändert geblieben. Aber 20 eV Stromwärme ist gewonnen worden auf Kosten der "eingeprägten Kräfte" bzw. der chemischen Energie in der Batterie. Ein Elektron, nahe der Stelle B' zwischen beide Pole gebracht, würde ohne äußere Einwirkung nach A' geführt werden (durch das elektrische Feld): korrekt für den Kondensatorstromkreis, aber absurd für den Gleichstromkreis mit einer Batterie!

Noch klarer wird die Situation für Wege von B' nach A' und zurück durch die Batterie. Zunächst sieht alles genauso aus, wie in (2) beschrieben. Im Kondensatorfeld, wo ein Potenzial existiert, müssten die Vorgänge auch genau so beschrieben werden. Tatsächlich aber muss für den Weg B' nach A' (grün) Arbeit hineingesteckt werden, Arbeit gegen Kräfte, die durch chemische Vorgänge entstehen. Auf dem Weg A' nach B' (rot) bewegt sich das Elektron "von allein" durch dieselben Kräfte. Die Situation ist ganz anders als bei elektrischen Kräften im Potenzialfeld.

Wenn man beim Gleichstromkreis nur von einem Potenzial spricht, ignoriert man den wesentlichen Teil des Gleichstromkreises, nämlich den "Pumpmechanismus", der für einen stationären Strom mit im Stromkreis vorhandenen Ladungen sorgt. Manche Vertreter der derzeitigen Diskussion von Oberflächenladungen gehen sogar soweit, dass sie das von Oberflächenladungen erzeugte elektrische Feld als Ursache für den Stromfluss behaupten, und nicht etwa das elektrische Feld, das von der Batterie ausgeht! Natürlich dienen Oberflächenladungen dazu, das elektrische Feld an die Leitergeometrie anzupassen. Ansonsten nehmen Oberflächenladungen nicht am Stromfluss teil und haben keine weitere Funktion. Insbesondere können sie keine Energie verlieren, die beim Stromfluss in Stromwärme umgewandelt werden könnte. Ihre geringe Zahl (wenn man den Rechnungen dazu glaubt) sollte auch schon stutzig machen!

Eine Kondensatorentladung sorgt für zeitlich begrenzten Strom, dabei baut sich das Feld ab, beim Gleichstromkreis dagegen fließt ein stationärer Strom, ohne dass sich das E-Feld nennenswert ändert. In der Elektrostatik, im Kondensator z.B., gibt es ein Potenzialfeld, aber keinen stationären Strom wie im Gleichstromkreis.

Eine allgemeine Definition der Spannung durch eine Potenzialdifferenz ist nicht möglich. Das wird besonders bei der Induktion offensichtlich. Hierfür ist typisch die Existenz einer Ringspannung, die bei einem Potenzialfeld verschwinden würde.

Bisher war ich immer der Meinung, dass man beim Gleichstromkreis (stationärer Strom) mit der Behauptung der Existenz einer Potenzialdifferenz zwar gegen prinzipielle physikalische Aussagen verstößt, dass sich das aber für praktische Situationen kaum auswirkt. Wenn jetzt aber sogar vorgeschlagen wird, in der Schule nicht existente "Äquipotenziallinien" zu zeichnen, lassen sich die Fehler nicht mehr übersehen. Man kann zwar die tatsächlichen Verhältnisse im Stromkreis beschreiben, indem man einen Teil der Wirkungen durch ein Potenzial erklärt, und die anderen Wirkungen offen lässt. Dann ist die Beschreibung aber nicht vollständig und kann eigentlich nicht "verstanden" werden.

Damit ist übrigens Versuchen der Boden entzogen, das nichtexistente Potenzial im Gleichstromkreis durch einen "elektrischen Druck" zu veranschaulichen (was auch immer das sein soll, vielleicht nur ein "harmloserer" Name für ein solches Potenzial?). Solche Versuche haben das zusätzliche Problem, dass die Nähe zu einer vermeintlichen Elektronenbewegung als Folge der Coulomb-Abstoßung untereinander mir zu groß erscheint, besonders, wenn man die (Leitungs-?)Elektronendichte durch eine Punktedichte visualisiert oder suggeriert, dass der "elektrische Druck" etwas mit der Elektronendichte im Leiter zu tun habe. Mit der Coulomb-Abstoßung zwischen den (wenigen) Oberflächenladungen und den vielen Leitungselektronen wird manchmal sogar argumentiert! Dagegen bewegen sich Elektronen im Gleichstromkreis wegen der "Pumpwirkung" der Stromquelle, im Modell wegen des (eingeprägten) elektrischen Feldes, das von ihr ausgeht, modifiziert durch Oberflächenladungen, und nicht wegen einer Coulomb-Abstoßung der Elektronen untereinander vom Pol mit der größeren Elektronendichte bzw. dem größeren "elektrischen Druck". Wo es in einem Stromkreis unterschiedliche Ladungsdichten gibt, habe ich in Modellrechnungen  gezeigt. Im wesentlichen ist die Ladungsdichte bei einem stationären Strom im Leiter (beim einfachsten Fall) überall konstant (außer bei Änderungen der Leitfähigkeit und des Querschnitts in einem schmalen Bereich)! Für eventuelle stationäre Raumladungen in Leiterabschnitten und Oberflächenladungen sagt das Kondensator-Modell, dass sie nicht am Stromfluss teilnehmen. Evtl. passen sie das elektrische Feld an. Und es gibt ja schließlich Leiter, die sich ganz anders verhalten, ohne ein dem Leiterverlauf folgendes E-Feld (z.B. im elektrolytischen Trog) oder Leiter, bei denen nicht am Rand ein Bereich großer Leitfähigkeit auf einen Isolator stößt (Das ist Voraussetzung dafür, dass das elektrische Feld dem Leiterverlauf folgt). Man misst bei ihnen trotzdem eine Spannung. Die Diskussion mit Oberflächenladungen ist hier nicht anwendbar.

Bei der Induktion gibt es in einer homogenen (kreisförmigen) Induktionsschleife mit überall konstanter Leitfähigkeit, wenn sich der eingeschlossene magnetische Fluss ändert, eine Spannung, einen Strom und mit Sicherheit kein elektrisches (skalares) Potenzial; zugegeben, auch keinen Gleichstrom. Nirgendwo gibt es "Ladungsanhäufungen", die Ursache für ein Potenzialfeld sein könnten. Die Ladungsträgerdichte im gesamten Stromkreis ist räumlich konstant. Nirgendwo werden Ladungen "getrennt". Durch das elektrische Wirbelfeld (sozusagen als "Pumpe") werden im Stromkreis vorhandene Ladungen verschoben, wobei Stromwärme entsteht. Die Spannung ist hier allerdings eine Ringspannung, die sich auch auf eine Verschiebungsarbeit zurückführen lässt, diesmal für einen geschlossenen Weg.

M.E. lässt es sich nicht vermeiden, die Spannung als "Verschiebungsarbeit pro Ladungsmenge" einzuführen. Ein erfolgreiches Konzept in der Schule besteht darin, sich dem schrittweise anzunähern. Die Definition passt dann sogar zur Ringspannung, wie sie für ein Verständnis der Induktion notwendig ist. Eine solche Definition ist dann auch kompatibel zur offiziellen Definition nach DIN 1324. Es hat sich bewährt, bei der Einführung zunächst von der Spannung einer Stromquelle (also einer Eigenschaft von ihr) zu sprechen (als Ursache für einen Strom) und erst später vom Spannungsabfall (als Folge eines Stroms), worauf dann die Definition als "Verschiebungsarbeit pro Ladungsmenge" folgt.

Anders als in der Physikdidaktik derzeit vielfach behauptet wird, haben "Oberflächenladungen" so gut wie nichts mit "Spannung" zu tun. Spannung als Potenzialdifferenz ist nur in der Elektrostatik eine sinnvolle Definition, die in der Schule eine geringere Rolle spielt.

Natürlich muss auch der Kreiswiderstand berücksichtigt werden.