Lernschwierigkeiten
können entstehen,
- wenn der Begriff einer "physikalischen Arbeit"
("Arbeit im physikalischen Sinn") oder "mechanischen Arbeit"
geprägt wird, der offenbar im Widerspruch zum "gesunden
Menschenverstand" steht,
- wenn nicht geklärt wird, dass es in der (Schul-)Mechanik
ausschließlich um "Verschiebungsarbeit" (kurz:
V-Arbeit) geht, also um Arbeit beim Verschieben eines
Gegenstands oder Körpers durch eine Kraft,
- wenn nicht klargemacht wird, dass auch in den
Konfliktfällen, z.B. beim Halten eines Gegenstands in gleicher
Höhe, Arbeit im physikalischen Sinn verrichtet wird, nur eben
keine Verschiebungsarbeit, u.a. weil hier keine Verschiebung
vorliegt,
- wenn ein Hokuspokus aufgebaut wird im Zusammenhang mit der
Frage, wer an wem Arbeit verrichtet, oder wenn behauptet wird,
dass ein Körper "an sich selbst" Arbeit verrichtet,
- wenn man zwar richtig darstellt, dass Arbeit einer
Energieänderung oder Energiedifferenz entspricht, wenn aber
(indirekt) behauptet wird, dass deshalb Arbeit immer
verzichtbar sei. Andere Arbeiten, z.B. Wärme Q, haben
schließlich auch ihren festen Platz in der Physik, und mit
Arbeit kann vielfach leichter argumentiert werden als mit
Energien.
|
Dabei ist klar:
- Der Begriff der Arbeit kümmert sich um
bestimmte (evtl. kleine) Energieänderungen zusätzlich zur
schon vorhandenen (evtl.
großen) Energie, also um den Prozess der
Energieänderung und nicht um den Bestand. Arbeit
betrifft den Prozesscharakter.
- Der Begriff der V-Arbeit bringt direkter das
Wirken einer Kraft bei einer Verschiebung
ins Spiel als die Energie.
- Zwar ist Arbeit immer eine Energiedifferenz.
Dennoch kann m.E. in der Schule die Argumentation mit der
Arbeit nicht durch eine Argumentation mit Energiedifferenzen
ersetzt werden, da u.U. die Entscheidung schwierig ist,
welche Energie beteiligt ist. Gerade beim elektrischen
Stromkreis wird hier häufig falsch mit einer elektrischen
Energie argumentiert. Dagegen hat der Arbeitsbegriff
(verkoppelt mit der Energieerhaltung) eher im Auge, welche
Energiedifferenz die Folge der Arbeit ist. Also in ΔW = U·I·Δt
nicht Ersatz der Arbeit durch eine Differenz von
elektrischen Energien, sondern z.B. Arbeit zur
Erwärmung des Stromkreises ("Stromarbeit"). Oder
Beschleunigungsarbeit = Arbeit zum Beschleunigung;
"Hub"arbeit = Arbeit zum Heben (ein für Schüler
unverständlicher und verwirrender Begriff), ...
- Arbeit ist ein nützlicher Begriff: Er
vermeidet komplizierte Fragestellungen (z.B. Wie entsteht
bei einer Bewegung mit Reibung innere Energie? Aus Arbeit
wird direkt innere Energie). Arbeit ermöglicht leichtere
Argumentation.
- Arbeit ermöglicht eine allgemeine Spannungsdefinition
in der E-Lehre, die sowohl eine Potenzialdifferenz als auch
eine Ringspannung (bei der Induktion) umfasst.
- In der Wärmelehre ist u.U. das Zusammenspiel
zweier Arbeiten, der mechanischen V-Arbeit W und der Wärme
Q, wesentlicher Bestandteil der Theorie.
- V-Arbeit wird nur dann verrichtet, wenn es
eine Verschiebung gibt und eine Kraft(-komponente) in
Richtung der Verschiebung.
|
Hinweise:
1. Wenn bei einer konstanten Kraft F
ein Körper um eine Verschiebung Δx = x - x0 verschoben
wird (von x0 nach x),
wird die Verschiebungs-Arbeit W(x) = F·Δx verrichtet. Dabei ist F die
Komponente der Kraft F in
Richtung der Verschiebung Δx, oder
F der Betrag der Kraft F und
Δx die
Komponente der Verschiebung in Richtung der Kraft.
2. I.A. gilt W(x)
= ∫ F(r)·dr
in den Grenzen von x0 bis x.
3. Immer muss dazu gesagt werden, bei welchem
Vorgang Arbeit verrichtet, wessen Energie dabei verändert wird.
4. Ist die Energieänderung (V-Arbeit) bei einer
Verschiebung von x0
nach x bekannt, so erhält man
die dazu nötige Kraft mathematisch durch Ableitung nach der oberen
Grenze x. Das gilt auch dann,
wenn die betrachtete Energieform unabhängig vom Ort ist, wie z.B. die
kinetische Energie, natürlich auch bei konstanter Kraft.
5. Einige "Klimmzüge" zu Feldkraft und
externer Kraft:
Durch eine äußere Kraft
Fext kann gegen die Feldkraft
F eines Potenzialfelds eine V-Arbeit Wext
verrichtet werden. Diese Arbeit ist zu unterscheiden von der Arbeit W,
die die Feldkraft
F verrichtet, wenn man den
Gegenstand im Feld sich selbst überlässt.
Wenn durch die äußere Kraft nicht auch kinetische Energie
zugeführt werden soll ("beliebig langsam"), müssen äußere Kraft
Fext und Feldkraft
F entgegengesetzt gleich sein:
Fext
= -
F (Kräftegleichgewicht,
KGG). Der Körper bewegt sich dann evtl. mit
konstanter Geschwindigkeit. Ebenso unterscheiden sich dann die Arbeiten
Wext und W allein
durch das Vorzeichen.
Andernfalls kann Wext
um den Anteil der kinetischen Energie von W verschieden sein.
Bei Vorliegen eines Potenzialfelds gilt F
= - grad Epot , bzw. eindimensional mit der
Ableitung:
F
= - dEpot/dx . Die
notwendige externe Kraft für das KGG ist dann Fext
= grad Epot . Das gilt z.B. für das
Gravitationsfeld oder für das statische elektrische Feld in einem
Kondensator.
Beispiel
Kondensatorfeld:
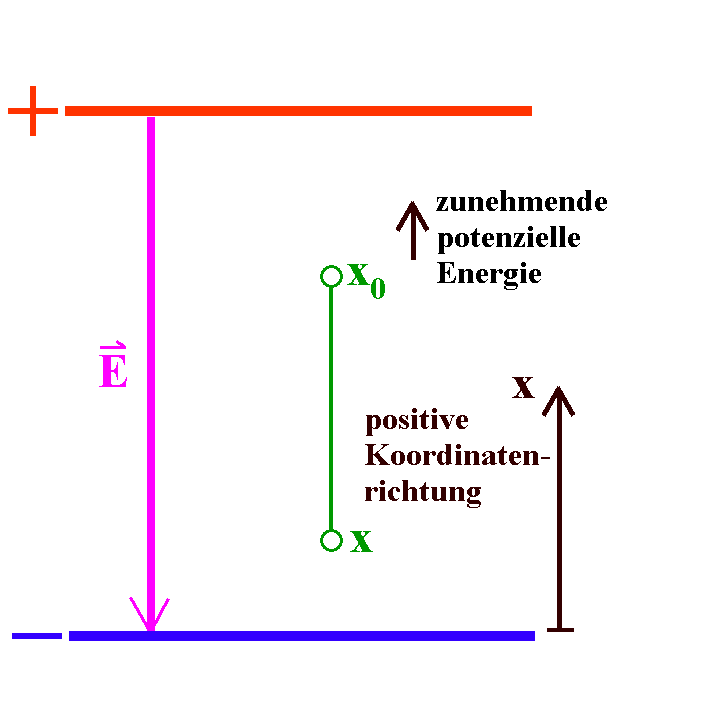
|
Das elektrische Feld
ist per definitionem von der positiven zur negativen
Kondensatorplatte gerichtet.
Der Koordinatenursprung liege
auf der negativen Platte. Die positive Koordinatenrichtung sei
zur positiven Platte hin gerichtet. Eine positive Probeladung
q erfährt darin eine (Feld-)Kraft F
= q·E, ebenfalls von
Plus nach Minus gerichtet, also in negative Richtung; q wird
von der positiven Platte abgestoßen und von der negativen
angezogen.
Um die Probeladung von der negativen zur positiven Platte zu
verschieben, muss Energie aufgewendet werden; die potenzielle
Energie der Ladung steigt in Richtung positive Platte. |
Vorgang
1: Die positive Ladung q ruhe an der Stelle x0
im Feld. Überlässt man sie sich selbst, wird sie durch die Feldkraft
F in Richtung zur negativen
Platte beschleunigt, wobei sie sich von x0
nach x bewegt. Das elektrische Feld
verrichtet dabei die positive Verschiebungsarbeit
W(x) = F·(x
- x0)
= q·E·(x
- x0)
> 0
[ wegen x
< x0 und E < 0 (von Plus nach Minus, gegen die
Koordinatenachse) ]
und
erhöht dabei die kinetische Energie der
Ladung. Die V-Arbeit wird der potenziellen Energie der Ladung
entnommen.
Vorgang
2: Umgekehrt, befördert man die positive Probeladung von x
nach x0 zurück (von der negativen Platte weg), braucht
man eine externe Kraft
Fext
in positive Richtung, die mindestens vom Betrag der Feldkraft
ist. Bei Kräftegleichgewicht wird der Probeladung potenzielle
Energie zugeführt, aber keine kinetische Energie. Die externe Kraft
verrichtet die V-Arbeit
Wext
= Fext·(x0
- x) > 0
[ wegen x < x0 ].
Dadurch erhöht sich die
potenzielle Energie der Ladung im Feld. Bei größerer externer Kraft
wird die Ladung auch noch beschleunigt, also auch die kinetische
Energie erhöht.
Vorgang
3: Möchte man auch beim Vorgang 1 eine externe Kraft ins
Spiel bringen, z.B. weil man die
Feldkraft
F
messen möchte, muss
Fext
entgegengesetzt zur Feldkraft sein. Will man durch Fext
keine kinetische Energie
zuführen, braucht man wieder KGG. Dann
gilt
Wext
= Fext·(x-
x0)
= -
F·(x-
x0)
= -
q·E·(x-
x0)
<
0
[ wegen x < x0 und E < 0 (von Plus nach
Minus, gegen die Koordinatenachse) ].
Fext
transportiert
Energie aus dem System; sie
verrichtet negative V-Arbeit. Sie entzieht diese
Energie der potenziellen Energie der Probeladung q, die sich dabei an
eine Stelle mit kleinerer potenzieller Energie (näher an der negativen
Platte) bewegt.
6. Mir bekannte Versuche, in der Schulphysik eine Kraft
durch die Steigung des "Strecke-Energie-Graphen" zu definieren (auch
x-E(x)-Graphen) erscheinen sehr unbefriedigend. Mit Hilfe der V-Arbeit
könnte man sie auf gesündere Füße stellen, aber sie bleiben
problematisch, weil nicht jede Energieänderung als Ursache eine Kraft
hat, weil m.E. kein anschauliches Verständnis einer Kraft vermittelt
wird. Es ist auch offen, wie sie das Präkonzept der Sch, Kraft sei die
Ursache für eine Bewegung, überwinden können.
( April 2016: ergänzt)
