.

a) Welleninterferenz bei Doppelspalt und Beugungsgitter

Welleninterferenz wurde von Thomas Young um 1800 entdeckt und diente lange Zeit als Nachweis für eine "Wellennatur" von Licht.

Damit die einfache Theorie des Doppelspalts funktioniert (Fraunhofer-Beugung), muss auf den Doppelspalt parallele Strahlung einfallen. Man kann entweder einen Laser nutzen, große Abstände oder eine Linsenanordnung zur Bündelung bei einer beliebigen Strahlungsquelle verwenden. Hier werden Interferenzversuche mit einem Doppelspalt beschrieben. Sie funktionieren ganz ähnlich mit einem Beugungsgitter. In der Schule wird als Beugungsgitter in der Regel ein Strichgitter aus sehr vielen parallelen und schlitzförmigen Spalten verwendet.

Ersetzt man die schlitzförmigen Spalte durch regelmäßig angeordnete punktförmige Öffnungen, erhält man ein Punktgitter, das in der Schule seltener verwendet wird.

Quasi ein Freihand-Versuch ist es, wenn du Laserlicht, z.B. von einem Laserpointer (Vorsicht, Gefahr für die Augen), durch den Doppelspalt treten lässt. Die Interferenzfigur wird auf einem Schirm (z.B. die Wand) aufgefangen ("objektive Betrachtungsweise", Abb. 1).

Abb. 1: Interferenzfigur auf dem Schirm, erzeugt durch einen Laserpointer, der durch einen selbst gebauten Doppelspalt strahlt. Die feinen Strukturen kommen vom Doppelspaltabstand d, die gröberen Strukturen - man erkennt im Foto nur noch links und rechts vom zentralen Maximum ein weiteres Maximum - kommen von Beugung und Interferenz an jedem der beiden Einzelspalte. Deren Abstände sind bestimmt durch die Spaltbreite b.

Ebenfalls ein Freihand-Versuch, wenn auch nur ein qualitativer ist es, wenn du durch einen Doppelspalt eine helle, quasi punktförmige Lichtquelle in einigen Meter Abstand betrachtest, z.B. den Lichtpunkt, den ein Laser auf eine Wand wirft, oder eine Leuchtdiode ("subjektive Betrachtungsweise"). In diesem Fall ist es allerdings nicht ganz einfach, die Minima und Maxima von jedem der beiden Einfachspalte von den feineren des Doppelspalts zu unterscheiden.

Bei beiden Betrachtungsweisen werden parallele Strahlen von der Lichtquelle genutzt, die durch die Spalte hindurch treten, dabei gebeugt werden und sich unter bestimmten "Ablenkungswinkeln" α zu Maxima überlagern. Bei der subjektiven Methode entstehen die Maxima im Auge; man nutzt die virtuellen Bilder auf einem Schirm oder Maßstab.

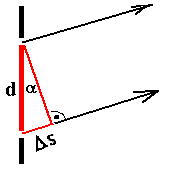Abb. 2: Messung des "Ablenkungswinkels" α bei der subjektiven Betrachtungsweise mit Hilfe des virtuellen Bilds auf dem Maßstab in der Nähe der LED. Unter dem "Ablenkungswinkels" α erscheint das virtuelle Bild des k-ten Maximums:   tan(α) = Δ/D        =>   α . Aus dem "Ablenkungswinkel" α und dem Gangunterschied Δs wird die Wellenlänge λ berechnet: sin(α) = Δs/d = k·λ/d mit  k = 0,1,2,3 ... für ein Maximum k-ter Ordnung => λ

Für eine beliebige Lichtquelle ist die Parallellicht-Erzeugung für die "objektive Betrachtungsweise" etwas aufwändiger, z.B. nach Abb. 3 oder Abb. 4. Genauso wie oben ergibt sich aus dem "Ablenkungswinkel" α die Wellenlänge λ.

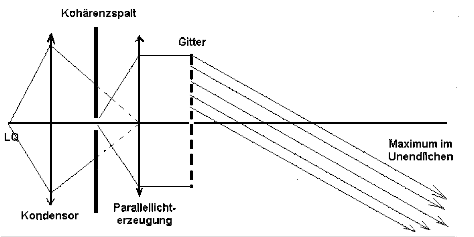Abb. 3: Anordnung zur Erzeugung von Parallellicht, das auf den Doppelspalt fällt (das Gitter ist durch den Doppelspalt zu ersetzen), "Standard-Anordnung" für Betrachtung der Interferenzfigur "im Unendlichen": Der Kondensor leuchtet für hohe Lichtstärke den Kohärenzspalt aus, und zwar so, dass die wahre Lichtquelle LQ in eine weitere Sammellinse abgebildet wird. Von jetzt ab dient der Kohärenzspalt als Lichtquelle. Dieser steht in der Brennebene der Sammellinse, die Parallellicht erzeugt, um Fraunhofer-Beugung zu ermöglichen. Im Parallellicht steht das Beugungsgitter; von ihm ausgehendes gebeugtes Parallellicht interferiert in großer Entfernung.

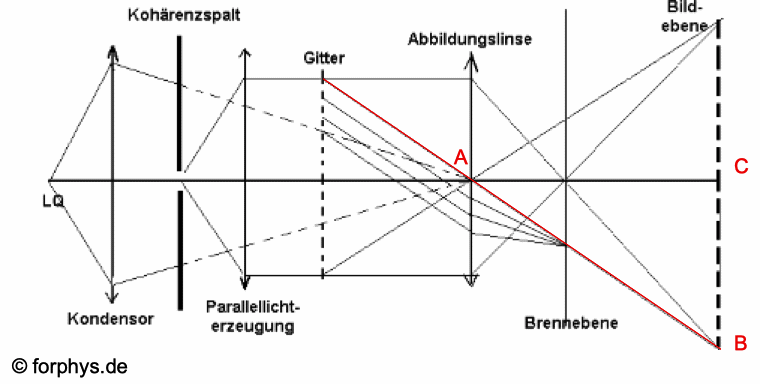Abb. 4: "Diaprojektor-Methode": Anordnung zur Erzeugung von Parallellicht, das auf den Doppelspalt fällt (das Gitter ist durch den Doppelspalt zu ersetzen), "Standard-Anordnung" für Betrachtung der Interferenzfigur im Endlichen: Der Kondensor leuchtet zur Erzielung  hoher Lichtstärke den Kohärenzspalt aus, und zwar so, dass die wahre Lichtquelle LQ in die Abbildungslinse abgebildet wird. Wie beim Diaprojektor verhindert das das Auftreten eines Bildes der Glühwendel und sorgt dafür, dass möglichst viel Licht von der wahren Lichtquelle durch die Abbildungslinse hindurch tritt. Der Kohärenzspalt steht in der Brennebene einer Sammellinse, die Parallellicht erzeugt, um Fraunhofer-Beugung zu ermöglichen. Im Parallellicht steht der Doppelspalt ("Gitter"); von ihm ausgehendes gebeugtes Parallellicht wird durch die Abbildungslinse in ihrer Brennebene gebündelt, wo es interferiert. Die Lage der Interferenzmaxima oder Minima ist durch den Mittelpunktsstrahl (rot) bestimmt, der die Abbildungslinse ungebrochen passiert. Diese Bedingung erlaubt die Bestimmung des Ablenkungswinkels α aus dem ΔABC.

Ähnlich zu Abb. 1 lässt sich Doppelspaltinterferenz mit Schallwellen nachweisen, am einfachsten mit Ultraschallwellen, weil dort die Spalt-Dimensionen entsprechend der kleinen Wellenlänge (ca. 8 mm bei 40 kHz) recht klein sind. Bei genügendem Abstand zwischen Doppelspalt und Ultraschall-Lautsprecher (Ultraschallwandler) bzw. Doppelspalt und Nachweis-Mikrophon (2. US-Wandler) ist die Strahlung in guter Näherung parallel.

Abb. 5: Doppelspalt-Versuch mit Ultraschall-Wellen, durchgeführt an der Deutschen Schule Algarve in Silves (Portugal)

Abb. 4: Doppelspaltversuch mit Ultraschall Der US-Sender wird durch einen Funktionsgenerator mit 40 kHz versorgt, das US-Mikrophon ist direkt mit einem Oszilloskop verbunden. Indem das US-Mikrophon am Lineal entlang geschoben wird, werden die Abstände der Minima bzw. Maxima registriert. Es sollten noch größere Abstände vom Doppelspalt gewählt werden um die Genauigkeit der Wellenlängenmessung zu erhöhen (Fraunhofer-Beugung!).

b) Hinweis auf Einteilchen-Interferenz

Es gibt auch eine Einteilchen-Interferenz. Lässt man nämlich ein einzelnes Quantenteilchen (Elektron, Photon, Atom, Fulleren-Molekül (ein so genanntes "Fußball-Molekül"), ... durch einen Doppelspalt laufen (G-R-A-Versuch), so wird es ganz auf einem Schirm in der Nähe eines bestimmten Punktes nachgewiesen. Wiederholt man den Versuch unter gleichen Bedingungen, wird das in der Regel ein anderer Punkt sein. Wiederholt man den Versuch aber sehr oft unter stets gleichen Bedingungen, so häufen sich die Nachweisorte an solchen Stellen, die den Maxima einer Interferenzfigur entsprechen, während an Stellen, die den Minima entsprechen, so gut wie keine Nachweise erfolgen. Man kann nicht vorhersagen, wo ein bestimmtes Quantenteilchen nachgewiesen werden kann; es gibt keine Gesetzmäßigkeit für den Einzelnachweis. Man kann nur eine Wahrscheinlichkeitsverteilung angeben für die möglichen Nachweisorte mit Maxima und Minima. Bei einem Einzelnachweis kann man auch keine Interferenz erkennen. Die Interferenzfigur wird bei Einteilchen-Interferenz erst bei sehr häufiger Wiederholung des gleichen Versuchs erkennbar.

Mathematisch kann man dieses Phänomen auch durch die Interferenz von "Wellenfunktionen" erklären (vgl. Interferenz). Diese breiten sich aber nicht wie die Teilchen im uns umgebenden Anschauungsraum aus, sondern höchstens in einem abstrakten "Konfigurationsraum" (was auch immer das ist). Die zugehörige Wellenlänge λ = h/(m·v) = h/p ist die deBroglie-Wellenlänge der verwendeten Teilchen (h Planck'sches Wirkungsquant, p = m·v Teilchenimpuls).

Mit Hilfe eines Diaglases, den Messern eines Einmal-Rasierers und einer Stecknadel lässt sich ein Doppelspalt für Laserlicht selbst bauen (Vgl. präparierter Doppelspalt, ohne die im Link erwähnten Polarisationsfolien).

(Vgl. auch mit einem Unterrichtskonzept zu einem modifizierten Doppelspalt: https://www.forphys.de/Website/qm/schulversuche/spaltanders.html. )

( Juni 2014 )