Viele Induktions-Versuche zeigen die Lenz'sche Regel:

Bei Stromfluss erfolgt die Induktion immer so, dass der Ursache der Induktion entgegen gewirkt wird.

Ursache der Induktion ist immer die Änderung eines magnetischen Flusses.

Eine anschauliche Interpretation der Lenz'schen Regel ist folgende:

"Spulen sind extrem konservativ. Sie versuchen immer, alles beim Alten zu belassen."

Betrachte folgenden Versuch:

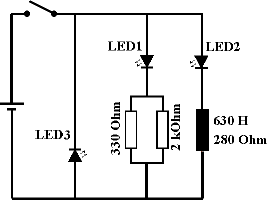Abb. 1: Ein Stromkreis soll sich in zwei parallele Zweige aufteilen, die beide den gleichen Ohm'schen Gesamtwiderstand Rg haben. Ein Zweig enthält ein Widerstands-Bauteil und ein Lämpchen L1 (Leuchtdiode LED1), der zweite Zweig eine große Spule und ein identisches Lämpchen L2 (LED2). Einschaltvorgang: Wird der Stromkreis im Schaltbild links geschlossen, leuchtet quasi sofort das Lämpchen L1 auf. Je nach Dimensionierung der Spule dauert es evtl. wenige Sekunden, bis das Lämpchen L2 gleiche Helligkeit erreicht hat. Erst nach dieser Zeit fließt in beiden Zweigen der gleiche Strom, trotz gleichen Gesamtwiderstands! Mit der Lenz'schen Regel ist eine qualitative Deutung klar: Weil sich mit dem Einschalten der Strom ändert, ändert sich auch das Magnetfeld in der Spule, also findet in ihr Induktion statt. Sie versucht den Anstieg des Magnetfelds zu verhindern. Einige Zeit lang gelingt ihr das auch. Mit etwas mehr Mathematik lässt sich das Phänomen auch quantitativ erklären: Beim Einschaltvorgang entsteht an der Spule eine Selbstinduktionsspannung Uind, die umgekehrtes Vorzeichen hat wie die Batteriespannung UB. Es liegen dann also zwei Spannungsquellen im Stromkreis, UB und Uind, die einander entgegenwirken und erst zusammen den Spannungsabfall an den Ohm'schen Widerständen von Spule (hier 280 Ohm) und Lämpchen (Rges·I = (Ri + RLED)·I) hervorrufen. Die Selbstinduktion lässt allmählich nach und spielt nach einiger Zeit keine Rolle mehr. Erst dann fließt in beiden Zweigen ein Strom der gleichen Größe. Den Ausschaltvorgang findest du hier oder bei der Lenz'schen Regel beschrieben. Die Selbstinduktionsspannung zu messen, ist dadurch erschwert, dass an der Spule nur die Kombination der Spannungen Uind + Ri ·I abgegriffen werden kann. Im Allgemeinen sollte die Grundschaltung oder Varianten verwendet werden.

Deshalb wird die folgende Vorgehensweise vorgeschlagen, sogar für einen Schülerversuch:

Es wird ein abschnittsweise linear wachsender und linear fallender Strom (ein Dreiecksstrom) durch eine Spule mit möglichst geringem Widerstand gepumpt. Die Spule reagiert darauf, indem sie eine Spannung induziert, eine Selbstinduktionsspannung, die unverfälscht gemessen wird.

Das wird ermöglicht mit einer so genannten Strompumpe, deren Details hier höchstens für deinen Lehrer interessant sind.

Für den Schülerversuch ist z.B. die Schülerversuchsspule mit 2 Wicklungen à 0,1 H und 1,5 Ω geeignet (oder bei Beschaltung: mit 0,4 H und 3 Ω). Die charakteristische Zeiten  T = L/R sind dann jeweils 0,06 s bzw. 0,13 s im Vergleich zu 2,2 s bei der Monsterspule.

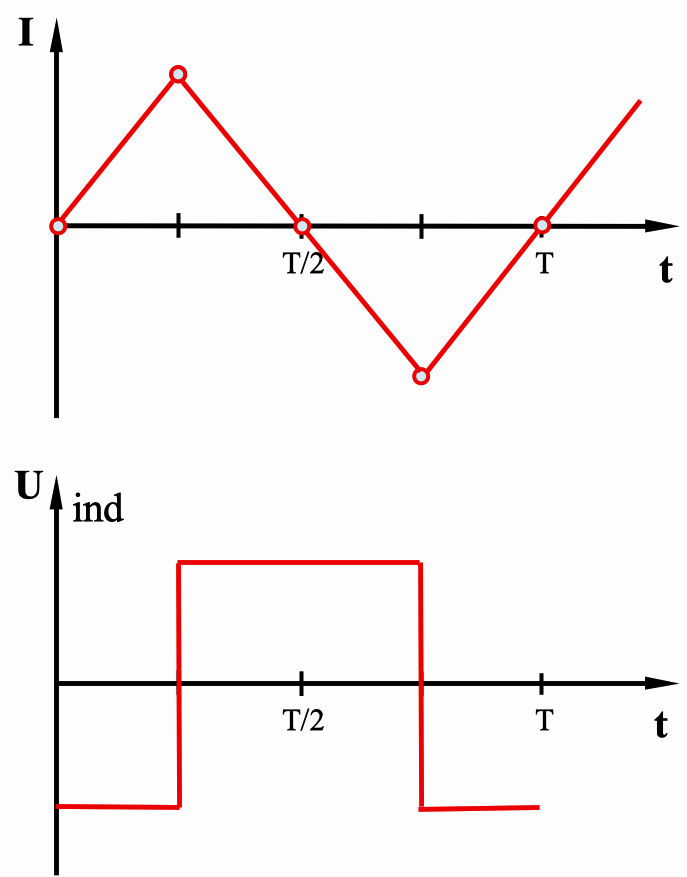Abb. 2: Schickt man einen dreiecksförmigen Strom (oben) durch eine weitgehend widerstandslose Spule, erzeugt diese eine abschnittsweise konstante Selbstinduktionsspannung (unten).*)

Im Realexperiment (hier wird die Spannung an der Spule U_L = -U_ind  gezeigt) mit einem Messinterface und dem Programm URI.exe:

Video (gif, ca. 10 MB) . Video (avi, ca. 2 MB) 

Es stellt sich heraus:

• ein linear veränderlicher Strom hat eine konstante Selbstinduktionsspannung zur Folge,
• wenn die Stromstärke steigt, hat die Selbstinduktionsspannung U_ind umgekehrtes Vorzeichen zur Spannung beim Fallen der Stromstärke,
• je schneller sich die Stromstärke verändert, desto größer ist der Betrag der Selbstinduktionsspannung,
• die konstante Steigung des t-I-Graphen im jeweiligen Zeitabschnitt ist proportional zur konstanten Selbstinduktionsspannung. Es gilt also

  U_ind  prop. ΔI/Δt

Zusammengefasst also  

mit der Induktivität L. Je größer die Induktivität L, desto größer ist der Betrag der Selbstinduktionsspannung /U/ bei einer bestimmten Änderungsgeschwindigkeit der Stromstärke ΔI/Δt. (Auf das Vorzeichen kommt es hier nicht an.)

Die Induktivität L hat die Einheit [L] = 1 V·s/A = 1 H ("Henry").   {Vgl. mit der Einheit der Kapazität:  [C] = 1 A·s/V = 1 F ("Farad")}.

Im Allgemeinen muss die Steigung des t-I-Graphen durch die Ableitung der Stromstärke I nach der Zeit, also dI/dt oder I^· (gelesen I punkt), ersetzt werden. So gilt allgemein:

Wenn Widerstände oder Lämpchen im Stromkreis in Reihe mit der Spule liegen, treten zusätzliche Spannungsabfälle auf, auch am Innenwiderstand R_i der Spule. Die Zusammenhänge zwischen Stromstärke und Spannungen sind dann weitaus komplizierter. Das wird bei Ein-/Ausschaltvorgängen an der Spule untersucht. Die Gesetzmäßigkeit (*) für die Selbstinduktionsspannung bleibt aber bestehen.

Im Allgemeinen, wenn der Spulenwiderstand nicht vernachlässigbar ist, sollte die Grundschaltung oder Varianten davon verwendet werden.

(Nicht für Schüler: Eine Induktionsspannung ist primär eine Ringspannung, die im geschlossenen Stromkreis einen Strom hervorruft. Sie kann dort gemessen werden durch die Stromstärke I: U = R·I. Die Ringspannung ist keine Potenzialdifferenz. Im offenen Stromkreis dagegen werden Ladungen an die Enden der Spule verschoben, so dass sich sekundär zwischen ihnen eine Potenzialdifferenz aufbauen kann von gleichem Betrag wie die Ringspannung. Durch diese Potenzialdifferenz kann mit einem geeigneten Voltmeter auch die Ringspannung gemessen werden.)

.

( Juni 2014 )