Hier geht es um eine der empfindlichsten Waagen der Welt. Du sollst die Masse m eines Elektrons bestimmen. Als Zwischenschritt sollst du erst die so genannte spezifische Ladung e/m ermitteln ("spezifisch": auf die Masseneinheit bezogen). Bei bekannter Ladung e des Elektrons kannst du dann die Masse m leicht bestimmen.

Im Fadenstrahlrohr (oder auch Wehnelt-Röhre) der Abb. 1 wird ein relativ scharf gebündelter Elektronenstrahl erzeugt, der zunächst geradlinig aus der Elektronenkanone austritt. Das Fadenstrahlrohr ist mit verdünntem Wasserstoff-Gas (mit einer kleinen Beimischung von Alkohol) gefüllt. Dadurch wird der Elektronenstrahl sichtbar. Die Elektronen bringen nämlich bei ihrem Durchtritt durch das Gas benachbarte Teile des Gases zu einem violetten Leuchten. Dabei werden die Elektronen an den Gasmolekülen etwas gestreut, der Strahl weitet sich auf und wird so um so deutlicher sichtbar.

Wenn du nun ein Magnetfeld geeigneter Richtung anlegst, krümmt sich der Elektronenstrahl, im Idealfall zu einem Kreis. Das ist dann der Fall, wenn das Magnetfeld B senkrecht auf der Ebene des Elektronenstrahls steht. Der Radius r der Kreisbahn bei gegebener Elektronenenergie e·U und gegebenem Magnetfeld B verrät die spezifische Ladung.

Du siehst das folgendermaßen:

(1) Aus der Beschleunigungsspannung erhältst du die kinetische Energie der Elektronen (mit dem Impuls p = m·v): p²/2m = e·U

(2) Die Lorentz-Kraft wirkt als Zentripetalkraft: m·v²/r = e·v·B

In Gleichung (2) lässt sich v herauskürzen: m·v = e·r·B . Das ist aber auch p = e·r·B (eine Gleichung, die du vielleicht von anderswoher kennst). Wenn du das in Gleichung (1) einsetzst, erhältst du:

e²·r²·B² / 2m = e·U

oder nach Kürzen mit e:

Zur Radiusmessung verwendest du am besten einen Spiegelmaßstab. Du schaust dann genau senkrecht auf die Kreisbahnebene, wenn du den "Faden" mit seinem Spiegelbild zur Deckung gebracht hast. Auf dem Spiegel markierst du Tiefstpunkt und Höchstpunkt der Kreisbahn und misst anschließend den Abstand als Durchmesser.

Abb. 1: Anordnung zur Messung der spezifischen Ladung mit dem Fadenstrahlrohr.

Abb. 2: So sieht der Fadenstrahl im verdunkelten Raum aus.

Du kannst dir auch ein Programm SPEZLAD.exe herunterladen, mit dem das Fadenstrahlrohr simuliert wird. Du kannst dann den Einfluss aller Parameter (U, B) auf den Kreisradius untersuchen.

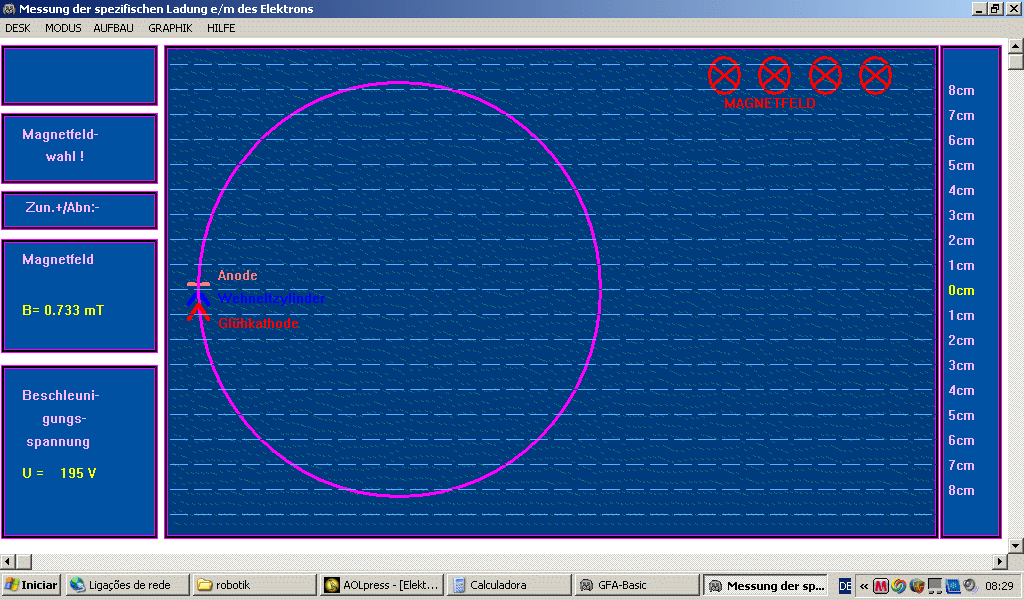Abb. 3: Simulierter Fadenstrahl nach dem Programm SPEZLAD.EXE. Du kannst e/m auf dem Bildschirm messen und auch Messreihen aufstellen, wie die Größen r, B, U voneinander abhängen. Thema für ein ergiebiges Kurzreferat! Einen kompletten Unterrichtstext dazu vom Autor und eine ältere Version des Programms SPEZLAD findest du hier.

.

( Mai 2014 )