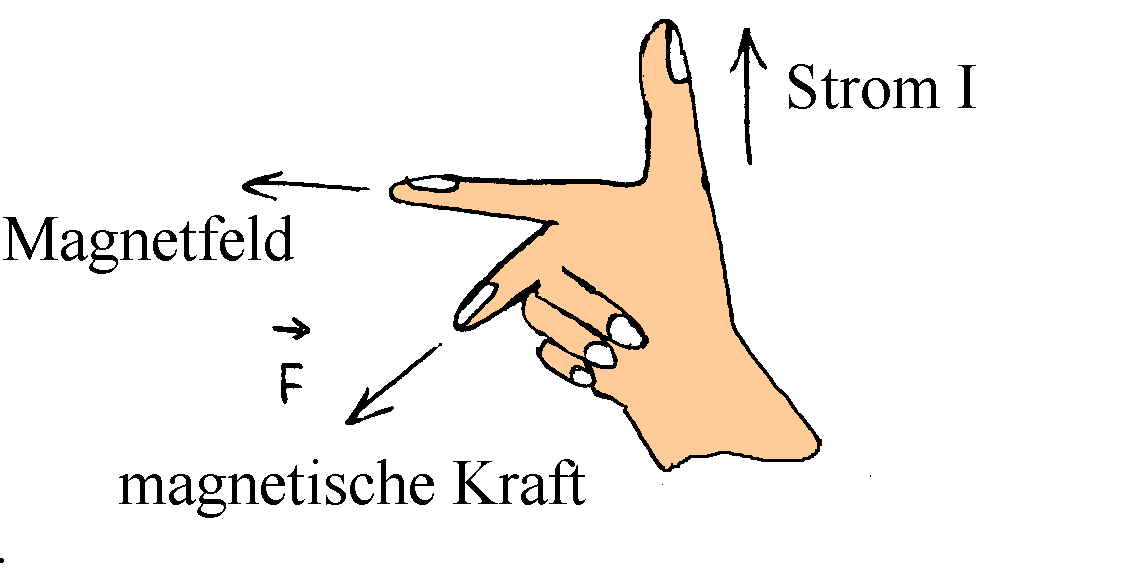
Der Daumen zeigt in Stromrichtung, der Zeigefinger in Richtung des Magnetfelds B und der Mittelfinger in Richtung der Lorentz-Kraft F.
|
SG090 Lorentz-Kraft ©
H. Hübel Würzburg 2013
|
Impres-sum |
1. Lorentz-Kraft:
Betrachte ein Bezugssystem (BZS) B, "in dem ein Magnetfeld B herrscht (zu messen ist) und in dem sich eine positive Ladung q mit der Geschwindigkeit v mit dem Betrag v << c bewegt" (c Lichtgeschwindigkeit). v soll nicht parallel zu B sein. B ist z.B. durch einen Permanentmagneten oder einen Elektromagneten erzeugt.Experimente zeigen, dass diese Ladung eine Kraft F erfährt mit folgenden Eigenschaften:
a) F ist senkrecht zu B und zu v. Es gilt die 3-Finger-Regel der rechten Hand.
b) Falls auch B senkrecht v, gilt für den Betrag:
|
F = q · v · B |
Das ist offenbar eine magnetische Kraft. Sie heißt nach ihrem Entdecker Lorentz-Kraft.
Die Lorentz-Kraft ist 0, falls
v parallel zu B ist.
Ein Beobachter, der in dem BZS B ruht, kann
diese Aussagen bestätigen.
Ein Beobachter dagegen, der mit
der Ladung mitbewegt ist,
der also in dem BZS A der Ladung ruht,
sieht eine Ladung, die in einem (leicht geänderten)
Magnetfeld B' ruht, die aber auch ein zusätzliches elektrisches
Feld E' mit (in guter Näherung) E' = v · B verspürt.
(Ohne nähere Erläuterung: B' und E' sind
eine Folge der Relativitätstheorie: Stichwort Lorentz-Transformation).
In diesem BZS A mit dem elektrischen Feld E' erfährt
die Ladung q eine elektrische Kraft F' und es gilt (in
guter Näherung) F' = q·E' = q ·v ·B. Für beide Beobachter ist die Kraft
die gleiche. Sie wird aber von beiden unterschiedlich, nämlich als magnetische
oder als elektrische Kraft, interpretiert.
Der Beobachter in BZS A misst außer E' ein Magnetfeld B', das bei kleiner Geschwindigkeit v weitgehend mit dem Magnetfeld B übereinstimmt, wie es der Beobachter B gemessen hat. Es spielt keine Rolle, da in ihm die Ladung q ruht.
Beide Beobachter sind sich einig, dass die Ladung eine Kraft von gleicher Größe erfährt, aber A behauptet mit Recht, dass es eine elektrische Kraft sei, während B genauso mit Recht behauptet, dass es eine magnetische Lorentz-Kraft sei.
| Wenn sich eine Ladung q mit der
Geschwindigkeit v im Vergleich zu einem BZS bewegt, in
dem ein Magnetfeld B gemessen wird, dann erfährt
q eine Lorentz-Kraft, wenn v und B nicht
parallel zueinander sind. Die Lorentz-Kraft steht immer senkrecht auf v und B. Sie ist maximal mit dem Betrag F = |q|·v·B (sonst jeweils Beträge), wenn v und B senkrecht aufeinander stehen. Ihre Richtung ergibt sich aus der 3-Finger-Regel der rechten Hand. |
3-Finger-Regel der rechten Hand:
 |
Maßgeblich ist die Stromrichtung
("technische Stromrichtung"), die nur bei einer positiven Ladung
mit der Bewegungsrichtung übereinstimmt. Bei einer negativen
Ladung ist sie also entgegengesetzt zur Bewegungsrichtung.
Der Daumen zeigt in Stromrichtung, der Zeigefinger in Richtung des Magnetfelds B und der Mittelfinger in Richtung der Lorentz-Kraft F. |
2. Bemerkung zu Bezugssystemen:
Betrachte eine einzelne elektrische Ladung q, die mit
einer Geschwindigkeit v bewegt ist.
Aber halt! Was soll denn das für eine Aussage sein? Ein
Beobachter A, der mit der Ladung mitbewegt ist, sieht eine ruhende
Ladung. Du (B) siehst vielleicht eine Ladung mit der Geschwindigkeit v
und ein dritter Beobachter C sieht eine Ladung, die sich mit v/2
bewegt. Das hängt vom Bewegungszustand des Beobachters ab. Um zu einer
eindeutigen Aussage zu kommen, müssen wir uns entscheiden, in welchem Bezugssystem
(BZS) wir argumentieren wollen. Also, eine korrekte Aussage wäre z.B.:
Betrachte eine Ladung q, die sich im Vergleich zu einem
Beobachter B (also in dessen BZS B) mit der Geschwindigkeit v bewegt.
Aber genauso richtig wäre es, vom Bezugssystem des Beobachters A aus zu argumentieren, einem BZS, in dem die Ladung ruht.
Du siehst also, ohne Angabe des BZS ist ein Gerede von einer "ruhenden" oder "bewegten" Ladung sinnlos, denn jede Ladung ist im BZS eines bestimmten Beobachters ruhend, im BZS eines anderen bewegt.
|
Jede elektrische Ladung ist bewegt, zugleich ruht jede elektrische Ladung. Das ist nur eine Frage des gewählten Bezugssystems. |
Beispiel:
Beobachter B sehe eine in seinem BZS bewegte Ladung, also einen elektrischen Strom, der sogar ein (schwaches) Magnetfeld erzeugt. Er sieht auch ein elektrisches Feld, das sich an seiner Position verändert, wenn die Ladung vorbeihuscht.
Beobachter A sehe dagegen eine in seinem BZS ruhende Ladung. Er kann ein elektrisches Feld feststellen, aber kein magnetisches.
Beide haben Recht!
So müssen wir also zur Kenntnis nehmen, dass ein und derselbe physikalische Vorgang von verschiedenen Bezugssystemen aus unterschiedlich gesehen und beschrieben wird, natürlich in allen BZS korrekt. Auch, ob ein Magnetfeld oder ein elektrisches Feld beobachtet wird, hängt u.a. vom Bezugssystem ab.
Einstein hat in seiner "Speziellen Relativitätstheorie" dazu nähere Angaben gemacht.
3. Hinweise:
a) Wenn du dich mit dem Vektorprodukt der Vektorrechnung auskennst, verstehst du, dass die Formel F = q · v x B allgemein für alle Orientierungen der Vektoren und alle Ladungsvorzeichen gilt und dabei in allen Fällen Aussagen über Betrag und Richtung der Lorentz-Kraft macht. In der wissenschaftlichen Literatur nimmt man häufig auch die elektrische Kraft q · E mit hinzu.
b) Z.B. aus der vektoriellen Darstellung ergibt sich für den Betrag der Kraft in allgemeineren Fällen:
F = |q| · v · B · sin(φ)
wenn v und B den Winkel φ einschließen. Wieder siehst du, dass F = 0, wenn v und B parallel sind (φ = 0).
c) Die Regel über die Lorentz-Kraft gilt in jedem Bezugssystem, in dem ein Magnetfeld B und die Bewegung einer Ladung gemessen wird. Dabei ist es völlig gleichgültig, in welchem BZS das Magnetfeld erzeugt wird, oder ob seine Quellen und Wirbel bewegt sind, ob es z.B. von einem rotierenden oder einem ruhenden Magneten ausgeht. Ganz gleich, wie der Magnet bewegt ist, dem von ihm erzeugten Magnetfeld sieht man das (lokal) nicht an, anders als man fälschlich vermuten könnte, wenn man sich nach dem "Stachelmodell" oder "Igelmodell" Magnetfeldlinien vorstellt, die am Magneten befestigt sind.
|
Es gibt keine Bewegung "gegen ein Magnetfeld", sondern nur eine "Bewegung gegen (oder in einem) ein Bezugssystem, in dem ein Magnetfeld B gemessen wird". |
 |
4. Im Internet fand ich
2020 ein Video mit nebenstehendem Titelbild zum B-Feld. Leider enthält es einige Fehler. Z.B. wird mit einer "Linken-Hand-Regel" eine falsche Richtung der Lorentz-Kraft hergeleitet, und auch das Feldlinien-Bild vermittelt einen falschen Eindruck. Obwohl die Kraft auf einen stromdurchflossenen Leiter eng mit der Lorentz-Kraft zusammenhängt, werden beide Kräfte üblicherweise unterschieden. Ich rate, das Video in dieser Form nicht anzuschauen |
( März 2014 ; September 2023 präzisiert)