 |
 |
|
SG053 Klassische Wellen ©
H. Hübel Würzburg 2013
|
Impres-sum |
|
|
|
||
| (1) Wenn du dir ein Video über Meereswellen anschaust, so fallen dir gleich zwei offensichtliche Bewegungen auf: eine Bewegung gegen das Ufer hin und eine Bewegung auf und ab, an denen offenbar die Wasserteilchen teilnehmen. | (2) Eine Wellenbewegung in einer Seilwelle oder einem "Federwurm" zeigt das noch deutlicher: einerseits bewegen sich kurze Abschnitte des Seils senkrecht zum Seil hin und her, andererseits schreitet der Bewegungszustand dieser Teilchen in Seilrichtung fort. Besonders auffällig wird das bei einem einmaligen Schlag auf das Seil quer zur Längsrichtung des Seils. |
 |
In einer Simulation (hier mit dem Programm WELLEN
des Autors) sind einzelne Massen durch Federn miteinander
verbunden.
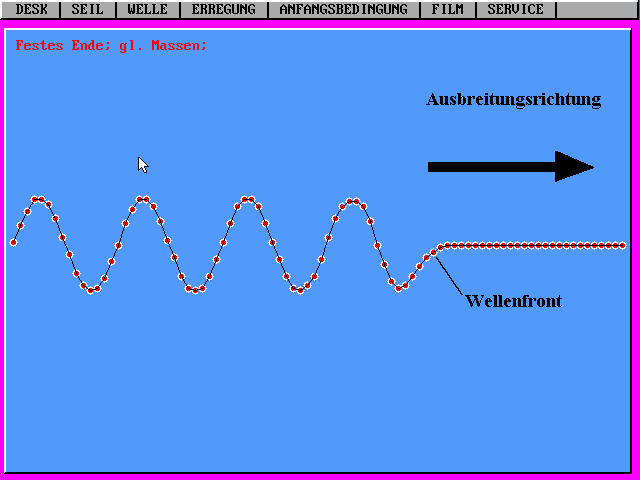
Hier kann man die beiden Bewegung ganz klar auseinander halten: 1. eine Bewegung der Massen quer zur Längsrichtung der Federkette und 2. ein Fortschreiten des Bewegungszustands längs der Federkette. Eine solche Welle heißt Querwelle oder Transversalwelle. Die Welle schreitet in "Ausbreitungsrichtung" fort. |
Die Massen der Federkette könnten auch in Längsrichtung schwingen. Dann bewegen sich die Massen gleichgerichtet oder entgegengesetzt gerichtet zum Fortschreiten des Bewegungszustands. Eine solche Welle heißt Längswelle oder Longitudinalwelle.
Wasserwellen sind häufig noch komplizierter: Bei bestimmten Typen kreisen Wasserteilchen um feste Mittelpunkte. Sie scheinen dann gleichzeitig auf und ab und auch vertikal hin und zurück zu schwingen. Auch in diesem Fall besteht die Welle darin, dass der Bewegungszustand in "Ausbreitungsrichtung" fortschreitet.
Schallwellen in Gasen sind Längswellen; in Festkörpern kann sich Schall auch mit Querwellen ausbreiten. Wellen auf Saiten sind in der Regel Querwellen.
Bei Schall heißt die Geschwindigkeitsamplitude der lokalen Teilchenschwingung Schallschnelle.
Wellenfront, Wellennormale, Gruppengeschwindigkeit,
Frontgeschwindigkeit und Phasengeschwindigkeit sind weitere wichtige
Begriffe.
Bei einer harmonischen Welle hängt die Auslenkung y sinusförmig von Ort x (längs der Ausbreitungsrichtung) und Zeit ab. Es gilt:
| y(x,t) = A·sin[2·π·(x/λ- t/T)] |
λ ist dabei die Wellenlänge, T die Schwingungsdauer der Teilchenschwingung. 2·π·(x/λ- t/T) heißt (Wellen-)Phase. Beachte: Zeit t und Ort x gehen ganz symmetrisch in die Phase ein. A ist die Wellenamplitude. Das ist die maximale Auslenkung eines Teilchens.
Die Ausbreitungsrichtung kannst du in der Gesetzmäßigkeit leicht feststellen: Betrachte dazu einen Punkt konstanter Phase, z.B. 0. Dann gilt also x/λ- t/T = 0 oder x = t/T·λ . Da hier alle Größen positiv sind, wächst x mit zunehmender Zeit: die Welle breitet sich in positive x-Richtung aus. Man hätte die Welle auch mit der Phase 2·π·(x/λ+ t/T) formulieren können. Dann würde gelten: x = - t/T·λ . Diese Welle breitet sich in Richtung negativer x-Werte aus. Du kannst Minuszeichen auch noch anders in die Phase einfügen. Wie gerade geschildert kannst du jeweils die Ausbreitungsrichtung feststellen.
c = λ/T hat die Dimension einer Geschwindigkeit. λ ist gerade die Strecke, die ein Punkt fester Phase in einer Periode T zurücklegt. Damit ist klar, dass c die Phasengeschwindigkeit ist. In der Schule heißt sie meistens - ungenau - Ausbreitungsgeschwindigkeit. Weil die Frequenz f = 1/T, gilt auch
| c = λ·f | f = 1/T |
Bei elektromagnetischen Wellen gelten ähnliche Beziehungen für die elektrische oder die magnetische Feldstärke (E bzw. B), z.B.
| E(x,t) = E0·sin[2·π·(x/λ- t/T)] |
Der Amplitudenvektor E0 entspricht dem Vektor der elektrischen Feldstärke E bei maximaler Auslenkung. Bei einer elektromagnetischen Welle schwingt im mechanischen Sinne nichts. Kennzeichnend ist die sinusförmige Abhängigkeit von Ort x und Zeit t. Elektromagnetische Wellen sind Transversalwellen.
| Eine Welle kann Energie, Nachrichten und Impuls transportieren. |
Bei elektromagnetischen Wellen und Schallwellen hat die Übertragung von Impuls nichts mit Masse zu tun (z.B. "Lichtdruck": durch Sonnenlicht erfahren z.B. Satelliten Impulsänderungen, die ihre Bahn beeinflussen). Auch der bei konstanter Schallintensität konstante Schallstrahlungsdruck hat mit Impulsübertragung zu tun, aber nichts mit Masse.
Bei allen klassischen Wellen ist die Energiedichte der Welle, also die Energie pro Volumeneinheit in einem kleinen Volumen ΔV um einen Punkt herum proportional zum Amplitudenquadrat.
| Das Amplitudenquadrat der Welle ist ein Maß für ihre Energiedichte in der Umgebung eines Beobachtungspunkts. |
Es gibt auch nichtperiodische Wellen. Dann bewegt sich ein einzelner Wellenberg oder ein Wellental in Ausbreitungsrichtung. Solche Wellen stehen im Zusammenhang mit den so genannten Solitonen.
( September 2013 )