Man kann sich einen rotierenden starren Körper vorstellen
als ein System von vielen einzelnen Teilchen, die in einer gewissen
Weise gemeinsam um ein Zentrum rotieren. Zum Glück gibt es
Gesetzmäßigkeiten und Verfahren, die eine Betrachtung dieser vielen
Kreis-Bewegungen durch die Betrachtung des Körpers als Ganzem ersetzen.
Ein rotierender starrer Körper rotiert um eine Achse. Das
kann eine feste Achse sein, die durch Lager festgehalten wird.
Das kennst du vom Fahrrad oder vom PKW. Du weißt aber auch, dass ein
Tennisball während seines Flugs ins gegnerische Feld sich um eine
mitbewegte Achse drehen kann. Man nennt sie eine "freie Achse".
Wozu braucht man überhaupt eine gelagerte Achse?
Die einzelnen Teilchen, die den ausgedehnten Körper
aufbauen, befinden sich bei der Rotation in einem beschleunigten
Bezugssystem; es können also auch Zentrifugalkräfte entstehen. Diese
spielen kaum eine Rolle, wenn die Drehung um eine Symmetrieachse
erfolgt, weil sich, getrennt durch die Achse, immer zwei Partner finden
lassen, die sich gegenseitig aufheben. Sie werden dann hier nicht weiter
diskutiert. Solche Achsen heißen Hauptträgheitsachsen.
Hauptträgheitsachsen sind also auch Symmetrieachsen. Ein Quader hat 3
Hauptträgheitsachsen. Andernfalls aber entsteht bei der Rotation eine
Unwucht, durch die eventuell zerstörerische Kräfte auf die Achslager
ausgeübt werden. Dagegen entsteht auf eine Hauptträgheitsachse keine
äußere Kraft. Die Achse muss dann nicht durch ein Lager festgehalten
werden; dies ist eine "freie Achse" um die eine "freie Drehung"
möglich ist. Bei einem kugelförmigen Tennisball ist jeder Durchmesser
eine Hauptträgheitsachse, um die eine freie Drehung erfolgen kann.
Ähnlich, wie das 2. Newton'sche Gesetz für eine
Translationsbewegung lautet: F = m · a , gilt auch für
das Drehmoment bei einer Drehbewegung:
M ist dabei der Vektor des Drehmoments,
ω* der Vektor der Winkelbeschleunigung (analog a =
Δv/Δt = v* , Zeitableitung von v, gilt
auch hier ω*= Δω/Δt bzw. Zeitableitung der Winkelgeschwindigkeit
ω) und Θ das so genannte "Trägheitsmoment".
Das Drehmoment ist senkrecht zur wirkenden Kraft und zum Hebelarm
gerichtet.
(Im Unterschied zu "der Zeitmoment" heißt
es das Trägheitsmoment und das
Drehmoment, weil das Wort vom lateinischen momentum herkommt.)
Bei einer Drehung um eine feste Achse oder auch eine
Hauptträgheitsachse sind Drehmoment M und Winkelbeschleunigung ω*
gleichgerichtet und Θ ist ein reiner Zahlenfaktor. Das Drehmoment
bewirkt dann eine zeitliche Änderung des Betrags von ω; der
starre Körper rotiert schneller oder langsamer. Die Richtung von
Drehimpuls und Winkelgeschwindigkeit bleiben dann konstant. Ohne
Drehmoment rotiert ein starrer Körper mit konstanter
Winkelgeschwindigkeit oder gar nicht.
(Bei einer Drehung um eine feste Achse sind auch
Drehimpuls L und Winkelgeschwindigkeit ω
gleichgerichtet: L = Θ·ω)
In anderen Fällen muss man bei der Interpretation
der Gleichung für das Drehmoment etwas vorsichtig sein, weil Θ nicht
immer als Zahlenfaktor aufgefasst werden darf (ohne weitere Erklärung:
"Trägheitstensor"). In diesem Fall sind L und ω auch
nur dann gleichgerichtet, wenn die Drehung um eine der drei möglichen
"Hauptträgheitsachsen" erfolgt. Eine freie Drehung ohne festgehaltene
Achse, ist nur um eine der Hauptträgheitsachsen möglich. Nicht alle
Hauptträgheitsachsen sind auch stabile Achsen. Ein Quader hat z.B. 3
Hauptträgheitsachsen, wovon nur die Drehung um die mit dem größten und
dem kleinsten Trägheitsmoment stabil ist.
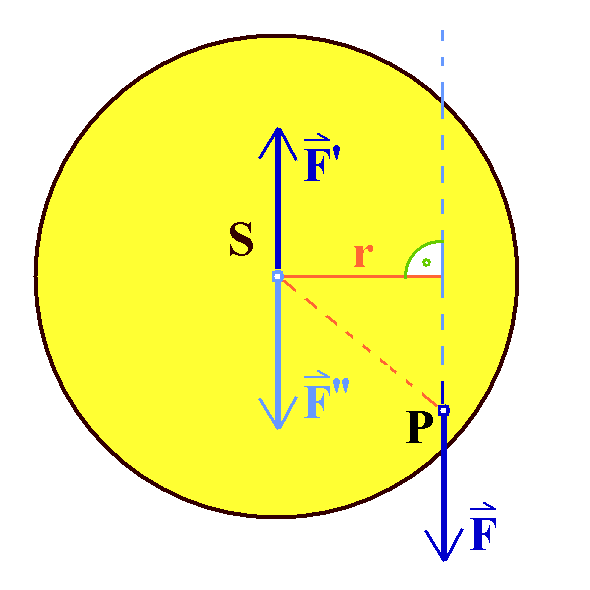 |
Falls an einem ausgedehnten Körper eine einzelne
Kraft F angreift, erzeugt diese ein Drehmoment und
versucht außerdem den Schwerpunkt zu verschieben.
Um die Wirkungen auseinander zu halten, kann
man zwei entgegengesetzt gleiche Kräfte F' und F"
hinzuaddieren, die sich gegenseitig aufheben, am Schwerpunkt S
angreifen und parallel zu F sind.
Sie lassen sich dann neu ordnen: F und
F' bilden ein Kräftepaar, das für ein Drehmoment M =
r·F bzgl. des Schwerpunkts S verantwortlich ist. Es verbleibt
die Kraft F", die eine geradlinige beschleunigte
Bewegung (eine Translation) des Schwerpunkts S bewirkt, wenn
sie nicht durch eine andere Kraft aufgehoben wird.
| Eine einzelne Kraft F auf einen
starren Körper lässt sich durch ein Drehmoment bzgl.
des Schwerpunkts und eine Kraft F" ersetzen,
die am Schwerpunkt angreift. |
|
Falls F nicht senkrecht zur Drehachse wirkt,
rüttelt F" an der Achse; wieder werden die Achslager evtl.
stark beansprucht, was man gerne vermeiden würde. Greift ein Paar von
entgegengesetzt gleichen Kräften an symmetrisch zum Schwerpunkt
gelegenen Punkten an, erzeugt das Kräftepaar kein Drehmoment bzgl. des
Schwerpunkts; bzgl der Beschleunigung des Schwerpunkts heben sich dann
die beiden Kräfte gegenseitig auf.
Der Drehpunkt D in der Abbildung ist vorgegeben,
wenn durch ihn eine feste Achse geht. In anderen Fällen kann man ihn oft
frei wählen. Dann müssen alle sonstigen beteiligten Größen auch auf
diesen bezogen werden. Wenn mehrere Kräfte auf einen Körper wirken,
empfiehlt es sich oft, als Drehpunkt D einen Punkt zu wählen, an dem
eine der Kräfte angreift, weil sie dann kein Drehmoment erzeugen kann.
 |
Schematisch:
Bewegung eines Astronauten in der
Schwerelosigkeit. Es wird angenommen, dass weder ein
Drehmoment noch eine Kraft auf ihn wirkt. Weiter wird
angenommen, dass senkrecht zur Zeichenebene eine
Hauptträgheitsachse liegt, um die also die freie Drehung des
Astronauten erfolgt.
Der Astronaut rotiert dann mit konstanter
Winkelgeschwindigkeit um seinen Schwerpunkt, der sich
gleichförmig geradeaus bewegt.
|
(September 2013)

