Greift eine Kraft an einem ausgedehnten Körper an, so kann sie - evtl. abgesehen von einer Verformung - zwei Wirkungen haben: Sie kann den Körper als Ganzen beschleunigen und sie kann ihn zusätzlich in eine Drehung versetzen. Um die beiden Effekte auseinander zu halten, denkt man sich die gesamte Masse des Körpers im Schwerpunkt konzentriert. Dann beschleunigt die Kraft den Schwerpunkt (in Richtung der Kraft). Wenn die Kraft aber außerhalb des Schwerpunkts am Körper angreift, so erzeugt sie zusätzlich ein "Drehmoment", das Ursache für eine beschleunigte Drehung um den Schwerpunkt ist.

(Im Unterschied zum (männlichen) Zeitmoment heißt es das Drehmoment, weil das Wort vom lateinischen momentum herkommt.)

Das Drehmoment spielt bzgl. einer Drehung eine entsprechende Rolle wie eine Kraft bzgl. einer (Translations-)Bewegung: Sie ist die Ursache für eine Winkelbeschleunigung.

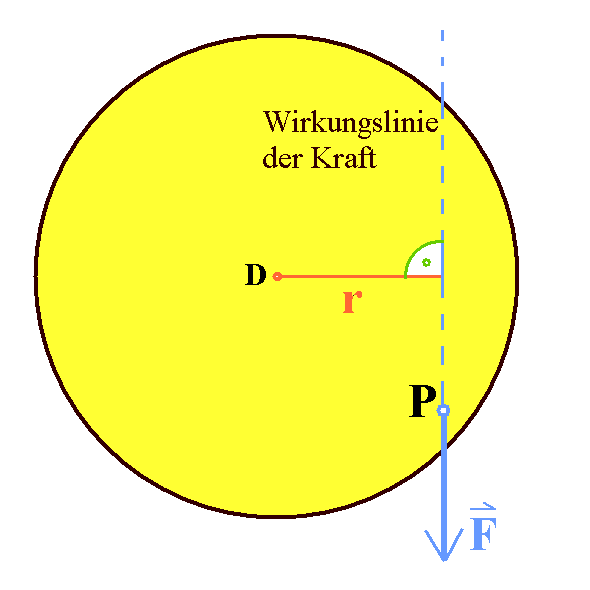Offenbar spielt der senkrechte Abstand des Drehpunkts D von der Wirkungslinie der Kraft F eine gewisse Rolle. Verschwindet dieser, entsteht auch kein Drehmoment und keine Winkelbeschleunigung. Dieser Abstand wird Hebelarm l (oder r) genannt. Dann gilt für den Betrag des Drehmoments M:    M = F·l     (Kraft x Hebelarm; M ist ein so genannter axialer Vektor. Er steht senkrecht auf der Kraft und dem Hebelarm). Die Einheit des Drehmoments ist dementsprechend:  [M] = 1 N·m (genauso wie bei der Energie, obwohl keinerlei Zusammenhang zwischen Drehmoment und Energie besteht).

Je nachdem, in welche Richtung das Drehmoment beschleunigt, unterscheidet man ein linksdrehendes und ein rechtsdrehendes Drehmoment. Die Bezeichnung ist eigentlich falsch, weil ein Drehmoment weder nach links noch nach rechts dreht. Ähnlich wie eine Bewegung keine Kraft erfordert (wenn sie einmal in Gang gekommen ist), erfordert auch eine Drehung kein Drehmoment. Wie die Kraft für eine Beschleunigung, ist das Drehmoment für eine Winkelbeschleunigung verantwortlich.

Ähnlich, wie das 2. Newton'sche Gesetz für eine Translationsbewegung lautet: F = m · a  (a =  Δv/Δt = v* , Zeitableitung von v), gilt auch für das Drehmoment bei einer Drehbewegung:

M = Θ · ω*     , wobei ω* der Vektor der Winkelbeschleunigung ist und Θ das so genannte "Trägheitsmoment". Bei einer Drehung um eine feste Achse oder eine Hauptträgheitsachse sind M und ω* gleichgerichtet und Θ ist ein reiner Zahlenfaktor. ( ω* = Δω/Δt = ω ^· , Zeitableitung von ω)

In anderen Fällen muss man bei der Interpretation dieser Gleichung vorsichtig sein, weil Θ nicht immer als Zahlenfaktor aufgefasst werden darf (ohne weitere Erklärung: "Trägheitstensor").

Der Drehpunkt D  in der Abbildung ist naheliegend, wenn durch ihn eine feste Achse geht. In anderen Fällen kann man ihn oft frei wählen. Dann müssen alle sonstigen beteiligten Größen auch auf diesen bezogen werden. Greifen mehrere Kräfte am ausgedehnten Körper an, dann ist es häufig geschickt, den Angriffspunkt einer der Kräfte als Drehpunkt D zu wählen, weil dann das zugehörige Drehmoment verschwindet.

.

( Oktober 2013 )