Normalerweise arbeiten Physiker nicht "blind". Sie stochern in der Regel nicht ziellos in der Natur herum in der Hoffnung so auf eine neue Erkenntnis zu stoßen. Sie haben meistens - spektakuläre Ausnahmen gibt es auch - eine Vorstellung von dem, was sie suchen, welche Eigenschaften es haben könnte, wie es mit anderen bekannten Dingen zusammenhängt.

Eine große Hilfe sind dabei Symmetrien. Es hat sich nämlich herausgestellt, dass die Natur in weiten Bereichen symmetrisch ist. Mit der Symmetrie sind nur ganz bestimmte Eigenschaften verträglich.

Beispiel 1:

Es geht um das elektrische Feld einer kugelförmigen Ladungsverteilung (im Extremfall um eine Punktladung). Wenn unsere Welt zweidimensional wäre, könnte das Feld, das die Ladung umgibt, eine von zwei symmetrischen Formen haben: eine radiale und eine azimutale mit ringförmig geschlossenen Feldlinien.

Abb. 1: Bei einer kreisförmigen Ladungsverteilung im 2-dimensionalen lässt die Symmetrie kreisförmig geschlossene Feldlinien zu	Abb. 2: Bei einer kreisförmigen Ladungsverteilung im 2-dimensionalen lässt die Symmetrie auch  radiale Feldlinien zu

Da die Welt nicht zweidimensional ist, ist keine dieser Varianten in der Natur realisiert.

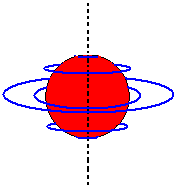
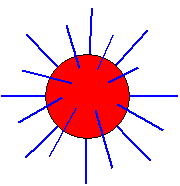
Aber im Dreidimensionalen verbleibt nur noch eine total kugelsymmetrische Situation, die radiale, weil andernfalls bestimmte Ebenen ausgezeichnet wären, in denen die ringförmig geschlossenen Feldlinien verlaufen. Dabei nutzt man die Tatsache, dass bei der Kugelsymmetrie keine Richtung und keine Ebene ausgezeichnet sein kann.

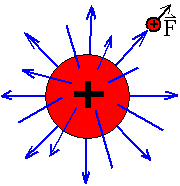
Abb. 3: Kugelförmige Ladungsverteilung im 3-dimensionalen lässt auch eine zylindersymmetrische Verteilung der Feldlinien zu, aber wodurch sollte die gezeichnete Achse bestimmt sein? Wenn das physikalische Problem eine solche Achse nicht vorgibt, ist dieser Fall ausgeschlossen.	Abb. 4: Kugelförmige Ladungsverteilung im 3-dimensionalen lässt bei voller Kugelsymmetrie nur radiale Feldlinien zu	Abb. 5: Kugelförmige Ladungsverteilung im 3-dimensionalen: eine von den beiden Möglichkeiten: radial von der Ladungsverteilung wegführende Feldlinien. Die Feldrichtung wird so definiert, wenn die zugehörige Ladung Q positiv ist.	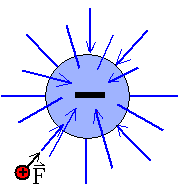Abb. 6: Kugelförmige Ladungsverteilung im 3-dimensionalen eine von den beiden Möglichkeiten: radial zur Ladungsverteilung hinführende Feldlinien. Die Feldrichtung wird so definiert, wenn die zugehörige Ladung negativ ist.

Bringt man eine weitere kleine positive Probeladung q  in das Feld, entsteht eine Kraft, eine Abstoßungskraft F (Abb. 5) bzw. Anziehungskraft (Abb. 6). Das Experiment zeigt, dass F mit zunehmendem Abstand r kleiner wird. Das Kraftgesetz könnte dann z.B. einen Faktor 1/r oder 1/r2 oder 1/ra (mit a > 0) enthalten. Diese Idee legt ein Experiment zur Entscheidung nahe. Es zeigt, dass tatsächlich F prop. 1/r2 gilt. Es ist naheliegend, dass die Größe der Kraft F von der Größe der Probeladung q abhängt, vielleicht ist sie sogar proportional zu q. Das 3. Newtongesetz lehrt weiter, dass zur Kraft von Q auf die Probeladung q eine entgegengesetzte Reaktionskraft gleicher Größe entsteht, die von q auf Q wirkt und bei Q angreift. Jetzt kommt erneut die Symmetrie ins Spiel: die Kraft muss symmetrisch in beiden Ladungen sein. Wenn die Vermutung F prop. q richtig ist, muss auch gelten: F prop. Q. Es gilt also vermutlich: F prop.   Q·q/r2  bzw. vektoriell:         F  prop Q·q/r2 r/r , wobei r/r ein Einheitsvektor in radialer Richtung ist. Jetzt hat man eine konkrete Vermutung, die jetzt entgültig im Experiment bestätigt werden muss. Das Experiment bestätigt die Vermutung und klärt dann auch noch die Größe der Proportionalitätskonstanten. Diese muss positiv sein. Denn, wenn Q und q unterschiedliches Vorzeichen haben, entsteht erfahrungsgemäß eine Anziehungskraft. Man hat das Coulomb-Gesetz erhalten, wobei man stark durch Symmetrieüberlegungen geführt wurde.

Beispiel 2: Es soll ein unendlich langer, dünner geladener Draht vorgegeben sein. Für den Verlauf von Feldlinien kann  man Zylindersymmetrie erwarten.

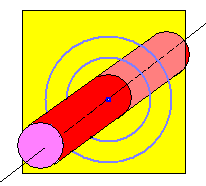
Beim elektrischen Feld einer linienförmigen (zylinderförmigen) Ladung ("unendlicher" Länge) sind auch im Dreidimensionalen azimutal, radial und axial verlaufende Feldlinien mit der (Zylinder-) Symmetrie des Problems verträglich. Die Natur hat sich für eine der Möglichkeiten in unterschiedlichen Situationen entschieden.

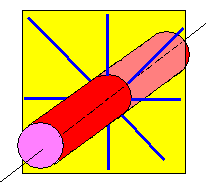
Abb. 7:  Bei einer linienförmigen Ladungsverteilung im 3-dimensionalen lässt die Symmetrie kreisförmig geschlossene Feldlinien zu	Abb. 8: Bei einer linienförmigen Ladungsverteilung im 3-dimensionalen lässt die Symmetrie  auch radiale Feldlinien zu, die auf dem Zylindermantel senkrecht stehen.	Abb. 9: Bei einer linienförmigen Ladungsverteilung im 3-dimensionalen lässt die Symmetrie auch axiale (tangentiale) Feldlinien zu

Welche Situation tatsächlich von der Natur realisiert ist, kann mit Symmetrieargumenten allein nicht entschieden werden. Bei einer statischen linienförmigen Ladung hat sie nur ein radiales elektrisches Feld realisiert (Abb. 8). Das hängt sehr eng mit der entsprechenden, ausschließlich möglichen Feldanordnung bei einer kugelförmigen Ladung zusammen. Von einer Verteilung punktförmiger Ladungen ausgehend könnte man "kausal" die tatsächlich beobachtete Feldverteilung erklären (Gauß'sches Gesetz: unmittelbare Folge ist das Coulomb-Gesetz).

Beispiel 3:

Ersetzt man die ruhende Ladung durch einen linienförmigen Strom, so erhält man ringförmig geschlossene magnetische Feldlinien ("kausal" erklärbar durch das Ampère'sche Gesetz; Abb. 8). Für diesen Fall hat sich die Natur aber zugleich auch für axiale tangentiale Feldlinien entschieden (Abb. 9), nämlich für Feldlinien des Vektorpotenzials A. Das ist kein Fall für die Schulphysik. Die Elektrodynamik lehrt, dass mit zunehmender Entfernung vom Zentrum des Leiters A in einer bestimmten Weise kleiner werden muss, so dass sich magnetische Feldlinien bilden, die den Strom ringförmig umgeben wie in Abb. 7. (Kenner wissen: B = rot A - was immer das auch heißen soll - führt dann zu ringförmig geschlossenen B-Feldlinien).

Beispiel 4:

Ersetzt man die linienförmige Ladung durch einen entsprechenden sich zeitlich ändernden magnetischen Fluss, dann umgibt sich dieser mit elektrischen Feldlinien (Abb. 7), die diesmal ringförmig geschlossen sind ("kausal" erklärbar durch das Induktions-Gesetz).

Abb. 10: Zu einem linienförmigen Strom I (Beispiel 3) gehört ein paralleles Vektorpotential A, das nach außen - vom Strom weg - stark abnimmt. Das ist identisch mit ringförmig geschlossenen B-Feldlinien, die den Strom nach Abb. 7 umgeben.

Beispiel 5:

Auch zu einer kugelförmigen Massenverteilung im dreidimensionalen Raum muss aus Symmetriegründen ausschließlich auf ein radiales Gravitationsfeld geschlossen werden.

Beispiel 6:

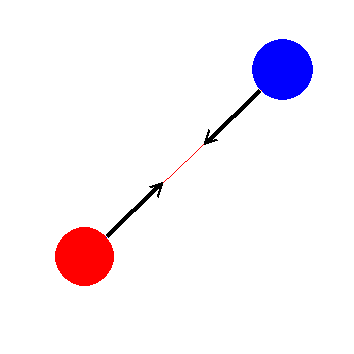
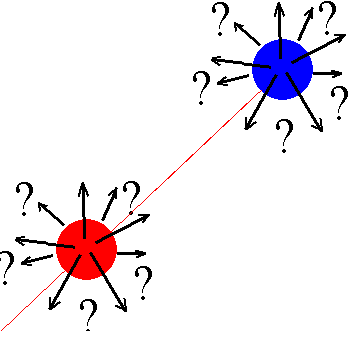
Bei zwei Punktladungen oder zwei punktförmigen Massen, oder auch kugelförmigen, muss man allein aus Symmetriegründen, da keines der beiden Objekte ausgezeichnet ist, auf gleichzeitig auftretende Kräfte schließen, die an beiden Objekten angreifen, wenn überhaupt Kräfte wirken. Da sie jeweils von einen Objekt ausgehen, müssen sie entgegengesetzt gerichtet sein. Sie können nicht "quer" zur Verbindungslinie der beiden Objekte gerichtet sein, da keine Richtung senkrecht zur Verbindungslinie ausgezeichnet ist.

Abb. 11: Mit der Symmetrie des Problems verträgliche Kraftrichtungen	Abb. 12: Mit der Symmetrie des Problems unverträgliche Kraftrichtungen

So ergibt sich das 3. Newton'sche Gesetz allein schon aus Symmetriegründen, wenn es überhaupt solche Kräfte gibt. Es könnte kausal durch den Impulserhaltungssatz erklärt werden. Welche Richtung die beiden Kräfte dabei jeweils haben (abstoßend oder anziehend), folgt aus der Beobachtung  und lässt sich z.B. - im Fall von Kugelladungen - mit dem "Kraftgesetz der Elektrostatik" kausal erklären.

Zylindersymmetrie liegt vor, wenn um eine Drehachse längs der Zylinderachse eine Drehung um einen beliebigen Winkel durchgeführt werden kann, die die Situation unverändert (invariant) lässt. Entsprechend lässt bei Kugelsymmetrie jede Drehung um jeden beliebigen Winkel und jede beliebige Achse die Situation unverändert (invariant). Man findet evtl. auch andere Symmetrietransformationen, die die vorgegebene Situation unverändert lassen.

Symmetrien in der Flora

	Abb. 13: Recht gut erfüllte 2-zählige Symmetrie. Gegenüber einer Drehung von 1800 ist die Blüte (weitgehend) invariant. Ohne die Staubgefäße läge eine 4-zählige Symmetrie vor. Die Symmetrie der Blüte ist genetisch festgelegt. Aber letzten Endes sind es auf molekularer Ebene physikalische Gesetze, die solche Symmetrien erzwingen. Zum Glück sind die Symmetrien, mit denen sich Physiker beschäftigen, häufig viel einfacher zu verstehen.
	Abb. 14: 5-zählige Symmetrie beim "nickenden Sauerklee": Gegenüber einer Drehung von 720 = 3600/5 ist die Blüte (weitgehend) invariant
	Abb. 15: Ungefähre 6-zählige Symmetrie bei einer Scabiose.  Gegenüber einer Drehung von 600 = 3600/6 ist die Blüte (weitgehend) invariant. In der Flora und Fauna sind Symmetrien häufig nur näherungsweise erfüllt, die Physiker sagen, sie sind "gebrochen". Auch in der Physik gibt es gebrochene Symmetrien, die ihre eigene - eventuell große - Bedeutung haben.

Symmetrische Tiere - Raumspiegelung

Abb. 16: Diese Spinne ist ein Beispiel für ein Tier, das (weitgehend) symmetrisch gegenüber Raumspiegelungen ist. Eine Raumspiegelung ist mit einer Achsenspiegelung im Zweidimensionalen verwandt. Statt an einer Spiegelachse wird hier im Dreidimensionalen an einer Ebene gespiegelt. Du kannst dir leicht vorstellen, wo diese im Foto liegen würde. Auch menschliche Gesichter sind (weitgehend) symmetrisch gegenüber Raumspiegelungen. Gut symmetrische Gesichter werden häufig als schön empfunden. Kleine Symmetriebrechungen, z.B. ein asymmetrischer Scheitel, betonen manchmal die sonst vorherrschende Symmetrie. Aber der menschliche Bauplan, wie er genetisch festgelegt ist, sorgt auch dafür, dass der Mensch nicht total symmetrisch gegenüber Raumspiegelungen ist. So gut wie alle Menschen haben das Herz auf der linken Seite, manche Menschen sind Linkshänder, manche Rechtshänder.

Kristallsymmetrien

Abb. 17: Bergkristall: Warum ergeben sich bei Kristallen so schön regelmäßige Formen, ebene Begrenzungsflächen mit ganz bestimmten Winkeln? Die regelmäßige (symmetrische) Anordnung der Gitterbausteine (Atome, Moleküle, Ionen, ... ) ist der eine Grund, Kräfte der Gitterbausteine auf die Nachbarn ein anderer.

In Kristallen sind Atome regelmäßig angeordnet. Auch in Modellen, bei denen jedes Atom durch eine kleine Kugel dargestellt wird, lassen sich leicht ähnliche regelmäßigen Anordnungen erreichen. In den Abb. 19, 20  werden zweidimensionale Modelle aus Glaskugeln gezeigt. Im Idealfall sind die Atomketten in alle drei Raumrichtungen beliebig weit fortgesetzt. Es gibt dann eine Vielzahl unterschiedlicher Richtungen, in die man fortschreiten kann, ohne dass sich die Umgebung ändert. Allerdings, man muss jeweils um eine ganz bestimmte Strecke fortschreiten. In den Fotos sind Beispiele solcher Strecken eingezeichnet. Die Gesamtheit solcher Translationen und Drehungen um bestimmte Winkel, die das Kristallgitter invariant lassen, ist typisch für eine bestimmte Kristallstruktur. Physiker schließen aus solchen Translationen, welche Impulse ein Kristallgitter aufnehmen kann, wenn Schall oder Licht in den Kristall gestrahlt werden.

	Abb. 18: Schüttelmodell aus Glaskugeln. Damit lassen sich verschiedene Aggregatszustände und der Aufbau von Kristallen simulieren und veranschaulichen.
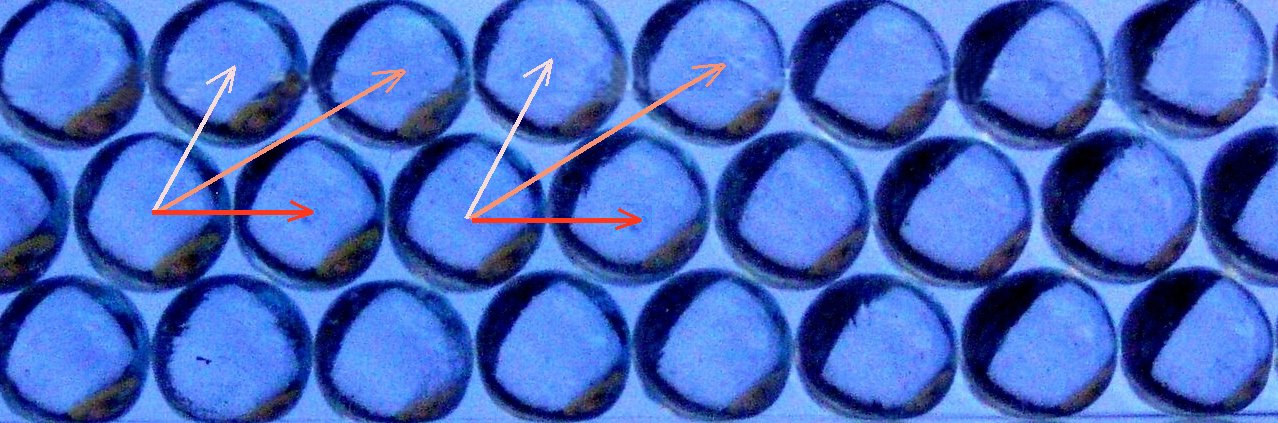	Abb. 19: Mit dem Schüttelmodell aus Glaskugeln erreichte "hexagonale" Anordnung der Kugeln als Modell für Atome in einem Kristall (Ausschnitt). Das Gitter bleibt invariant bei Translationen, z.B. um die eingezeichneten Strecken, oder bei Drehungen um 600, 1200, ... um das Zentrum einer Kugel.
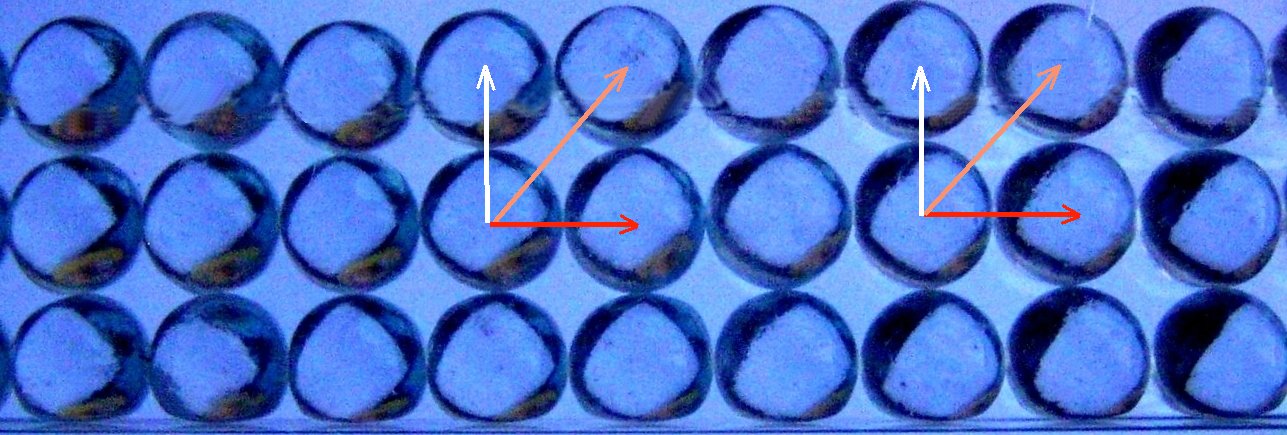	Abb. 20: Mit dem Schüttelmodell aus Glaskugeln erreichte "kubische" Anordnung der Kugeln als Modell für Atome in einem Kristall (Ausschnitt) Das Gitter bleibt invariant bei Translationen, z.B. um die eingezeichneten Strecken, oder bei Drehungen um 900, 1800, ... um das Zentrum einer Kugel.

Ebene Welle

Betrachte eine mechanische Welle: Man muss dann zwischen den Richtungen der Teilchenschwingungen und der Ausbreitungsrichtung der Welle unterscheiden. Da außer der Ausbreitungsrichtung keine weitere Richtung ausgezeichnet ist, ist mit der Symmetrie des Problems nur verträglich, dass die Teilchen in Ausbreitungsrichtung schwingen (Longitudinalwelle) oder senkrecht dazu (Transversalwelle). Dass die Teilchen in eine bestimmte Richtung transversal schwingen, setzt eine "Symmetriebrechung" voraus, die z.B. durch einen Polarisator oder die Sendeantenne erfolgt.

Translationsinvarianz im Raum - Impuls

Bei einer ("unendlich" ausgedehnten) ebenen Welle kann man um eine ganze Wellenlänge oder mehrere ganze Wellenlängen längs der Ausbreitungsrichtung fortschreiten ohne dass sich das "Wellenbild" ändert. Das hängt mit einem Impuls zusammen, den die Welle in Ausbreitungsrichtung transportiert. (Der "Wellenzahl-Vektor" mit dem Betrag k = 2.p/l ist proportional zum Impuls.) Er ist bei diesem Vorgang zeitlich konstant: Translationsinvarianz im Raum ist verbunden mit einer Impulserhaltung.

Bei mechanischen Wellen durch einen Kristall (Phononen) sind wegen der Kristallsymmetrie nur bestimmte Richtungen und Wellenlängen zugelassen. Dem entsprechen ganz bestimmte zugelassene Impulse.

(Hinweis: Schallwellen und elektromagnetische Wellen übertragen einen Impuls z.B. auf ein Metallplättchen, auf das sie treffen. Das kann man bei elektromagnetischen Wellen mit der Lorentz-Kraft erklären. Es gibt aber keinen notwendigen Zusammenhang zwischen dem Impuls einer Welle und einer Masse.)

Drehinvarianz bei einer kugelsymmetrischen Ladungs- oder Massenverteilung - Drehimpuls

In Beispiel 1 bzw. Beispiel 5  hattest du dir schon überlegt, dass mit der kugelförmigen Ladungs- oder Massenverteilung nur eine radiale Kraft auf einen zusätzlichen kleinen Probekörper (Probeladung) verträglich ist. Man spricht von einer Zentralkraft auf den Probekörper. Eine Folge von dieser ist - wie hier nicht gezeigt werden soll - ein konstanter Drehimpulsvektor L (was immer das ist).  Dass seine Richtung konstant ist, hat in der klassischen Physik zur Folge, dass sich der Probekörper nur in einer festen Ebene um den Zentralkörper bewegen kann. Dass sein Betrag auch konstant ist, hat zur Folge, dass das 2. Kepler-Gesetz gilt: Der Fahrstrahl überstreicht in gleichen Zeitabschnitten gleiche Flächen. So führt also die Drehinvarianz wieder zu einer Erhaltungsgröße, den Drehimpuls.

Es stört nicht, dass die resultierende Planetenbahn nicht unbedingt drehsymmetrisch ist: Wir kennen vielmehr die Ellipsenbahnen der Planeten. Bei einem konkreten Planeten kommen nämlich zwei Dinge zusammen: das drehinvariante Naturgesetz (hier das Gravitationsgesetz), das sehr viele Bahnen ermöglicht, die in ihrer Gesamtheit Drehinvarianz verraten, und die bei der Entstehung des Planeten geltenden Anfangsbedingungen, durch die von den vielen möglichen Bahnen eine konkrete ausgewählt wurde.

Dass überhaupt geschlossene Bahnen möglich sind, liegt am speziellen Gravitationsgesetz mit seiner 1/r²-Abhängigkeit vom Abstand r zwischen Sonne und Planet. Bei anderen Kraftgesetzen, die auch drehsymmetrisch sind, würden nicht einmal geschlossene Bahnen existieren. Das ist schon beim Planeten Merkur der Fall als Folge der relativistischen Änderung seiner Masse mit der Geschwindigkeit.

Bau des Wasserstoffatoms

Du hast - vielleicht in der Chemie - schon von Orbitalen gehört, mit denen man Orte beschreiben kann, an denen man das eine Elektron eines Wasserstoff-Atoms besonders häufig finden kann. Das zugrundeliegende Naturgesetz ist das Coulomb-Gesetz für das elektrische Feld des positiven Atomkerns, in dem sich das negative Elektron befindet. Das Coulomb-Gesetz ist kugelsymmetrisch; das bleibt auch in der Quantenphysik so, mit der ein solches H-Atom beschrieben werden muss. Der Drehimpuls ist also jeweils konstant (Bahndrehimpuls).

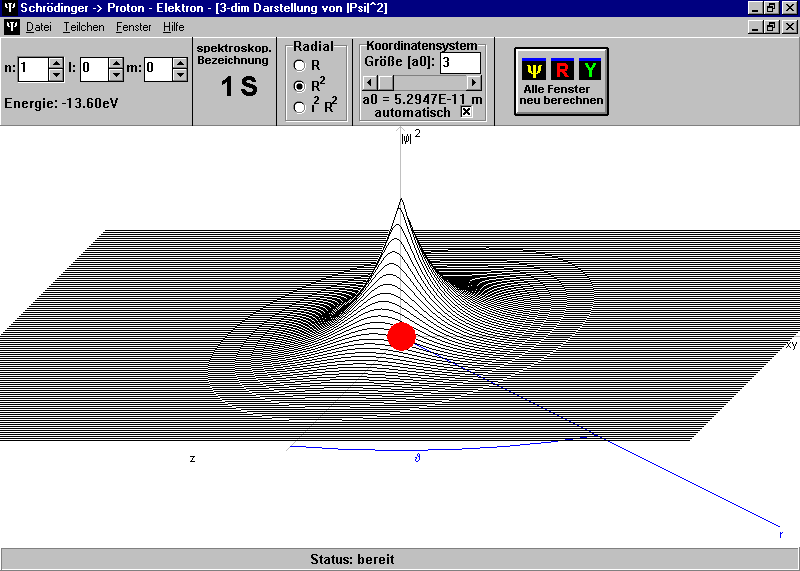	Abb. 21: 3-dimensionale Darstellung des 1s-Orbitals eines H-Atoms, erzeugt mit dem Programm SCHRÖDINGER.exe von der Uni Würzburg. Wenn sich in der Graphik ein Punkt weit über die xy-z-Ebene erhebt, ist dort das Elektron besonders häufig zu finden. Die Position des Atomkerns ist rot markiert.
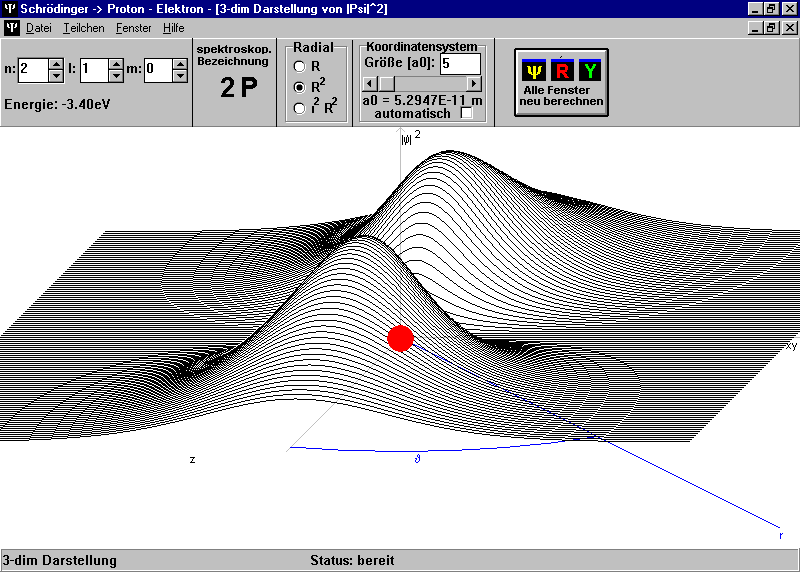	Abb. 22: 3-dimensionale Darstellung eines 2p-Orbitals eines H-Atoms, erzeugt mit dem Programm SCHRÖDINGER.exe von der Uni Würzburg. Wenn sich in der Graphik ein Punkt weit über die xy-z-Ebene erhebt, ist dort das Elektron besonders häufig zu finden. Die beiden Enden der Keule sind bei diesem Zustand offenbar in z-Richtung orientiert.

Manche der Orbitale sind auch kugelsymmetrisch; sie gehören zu den möglichen Zuständen des H-Atoms mit dem konstanten Drehimpuls 0 (so genannte s-Zustände; Abb. 21). Andere Zustände werden durch die Drehimpulsquantenzahl 1 beschrieben (so genannte p-Zustände; Abb. 22). Die Orbitale sehen hier wie Keulen aus, die in x- oder y- oder z-Richtung orientiert sind. Sie sind offenbar trotz des kugelsymmetrischen Naturgesetzes nicht kugelsymmetrisch. Aber wie sind die x-, y-, z-Achsen im Raum orientiert? Wenn das z.B. durch ein Magnetfeld oder das elektrische Feld benachbarter Atom in einem Kristall (teilweise) festgelegt ist, ist die Kugelsymmetrie aufgehoben; man braucht dann keine Kugelsymmetrie der Zustände erwarten. Ist das nicht festgelegt, sind alle 3 Raumrichtungen gleichwertig. Misst man jetzt den Ort des einen Elektrons wird man ihn einmal hier, einmal da messen, zwar jeweils in einem bestimmten Orbital, aber mal von diesem, mal von jenem Atom mit dieser oder jener Orientierung. Die vielen Messergebnisse, die uns schließlich ein Bild vom Atom verschaffen, scheinen drehsymmetrisch verteilt zu sein. (Die Physiker sagen, die Wahrscheinlichkeitsdichten der 3 unterschiedlich orientierten p-Zustände überlagern sich. Die Summe zeigt Kugelsymmetrie.)

Bei chemischen Bindungen ist aber gerade der Fall einer Richtungsauszeichnung gegeben. Deshalb hilft es den Chemikern mit Recht beim Verständnis solcher Bindungen, wenn sie nur einzelne, nicht kugelsymmetrische p-Zustände betrachten. Deshalb sprechen Chemiker so gern über "Keulen".

Zeitinvarianz - Energie

Misst man von einem klassischen Teilchen immer wieder zu verschiedenen Zeitpunkten die Energie und verhält sich dabei die Energie unverändert (invariant), so gilt offenbar der Energieerhaltungssatz. Auch ist eine elektromagnetische Welle invariant gegenüber einem Fortschreiten in der Zeit um eine Schwingungsdauer T. Zu T gehört die Frequenz f und h.f ist die Energie eines Photons. Die Translationsinvarianz gegenüber der Zeit beim Fortschreiten um eine Schwingungsdauer T hängt offenbar zusammen mit der Konstanz der Energie E von Photonen. Allgemein hängt die "Translationsinvarianz gegenüber einer Translation in der Zeit" mit der Energieerhaltung zusammen, auch in viel allgemeineren Fällen.

In allgemeineren Fällen muss die Translationsinvarianz sorgfältiger definiert werden. Man hat dabei auch weniger einen einzelnen Vorgang, wie die erwähnte Bewegung, als vielmehr Naturgesetze im Auge. Dass Naturgesetze sich "bei Zeittranslationenen invariant verhalten", heißt, dass sie zu allen Zeiten in gleicher Weise gelten. Das ist der Grund dafür, dass aufeinanderfolgende Messungen in der gleichen Situation immer bis auf (hoffentlich kleine) Messfehler immer das gleiche Ergebnis liefern, dass sie "reproduzierbar" sind. Würden sich die Naturgesetze im Laufe der Zeit verändern, könnte man weder die Bewegung einer Raumstation noch eines Planeten für eine gewisse Zukunft vorhersagen. Eine Wettervorhersage wäre unmöglich. Noch könnte man rückwärts entscheiden, wie alt unser Weltall ist (man geht normalerweise von ca. 15 Mrd. Jahren aus), noch könnte man zurückrechnen, wie das Weltall kurze Zeit nach dem Urknall ausgesehen hat. "Invarianz der Naturgesetze gegenüber Zeittranslationen" ermöglicht erst Wissenschaft. Ihre Erfolge zeigen, dass diese Invarianz wohl erfüllt ist.

Zeitspiegelung

In der Newtonschen Mechanik lernst du, dass man eine Bewegung für alle Zukunft vorherberechnen kann, wenn die wirkende Kraft und die Anfangsbedingungen (Ort und Geschwindigkeit, z.B. jetzt) bekannt sind. Unter dem Einfluss der Gewichtskraft fällt der Stein von oben nach unten, genau vorher berechenbar. Ein am Ort 0 m aus der Ruhe startender Stein hat bei uns nach 2 s eine Strecke von ca. 20 m durchfallen und dabei eine Geschwindigkeit von ca. 20 m/s erreicht. Aber in der gleichen Weise kannst du die Bewegung in die Vergangenheit zurückverfolgen; du brauchst nur negative Zeiten verwenden. Zur Zeit t = - 2 s (statt t = 2 s) soll sich dann der Stein ebenfalls am Ort 20 m befinden, aber die Geschwindigkeit - 20 m/s haben. - 2s bedeutet 2s vor dem oben erwähnten Startpunkt bei t = 0. Negative Geschwindigkeit bedeutet eine Bewegungsrichtung nach oben. Also, der - vorher so genannte - Startort 0 m zur Zeit 0 s wird erreicht, wenn der Stein 2 s vorher eine Geschwindigkeit von - 20 m/s nach oben hatte und sich am Ort 20 m befand. Nichts besonderes also. Die Newtonsche Mechanik wie alle Gesetze der klassischen Physik sind "invariant gegenüber einer Zeitumkehr" (oder einer Zeitspiegelung). Sie befasst sich auch mit recht einfachen Gegenständen, z.B. dem Stein, der sich näherungsweise sogar wie ein Massenpunkt verhält.

Aber, wenn du auch berücksichtigst, dass der Stein nach 2 s auf dem Boden zerschellt und in viele Splitter zerspringt, die sich auch noch geringfügig erwärmen, müssten sich bei - 2s demnach viele Splitter eines Steins zu einem Stein vereinigen und ihm auch noch eine Geschwindigkeit von -20 m/s nach oben mitgeben, wobei sie sich und der umgebende Boden abkühlen. Um hier Zeitumkehrbarkeit zu beurteilen reicht die Idealisierung als Massenpunkt nicht mehr aus. Dann muss man schon den Stein als großes ausgedehntes Gebilde mit einer bestimmten Zusammensetzung, Form und bestimmten Kräften zwischen seinen Bestandteilen (Atomen, Molekülen oder Ionen) berücksichtigen. Solche Körper werden als makroskopisch bezeichnet.

In solchen doch schon etwas komplexeren Situationen widerspricht Zeitumkehrinvarianz aller Erfahrung. Eine Vase zerschellt auf dem Boden in Scherben, aber niemals finden sich Scherben "von allein" zusammen um eine ganze Vase zu bilden. Wenn in einem Raum ein Fläschchen mit einem stark riechenden Gas geöffnet wird, durchmischen die Moleküle dieses Gas in kurzer Zeit die Luft des ganzen Raums. Aber niemals sammeln sich diese Moleküle wieder in der geöffneten Flasche.Wenn ein Topf mit heißem Wasser in ein kaltes Zimmer gestellt wird, kühlt sich das Wasser ab und wärmt den Raum auf. Aber niemals kehrt sich der Vorgang um und erwärmt "von allein" das Wasser im Topf, wobei sich der Raum abkühlt. In der Natur der makroskopischen Körper scheint eine eindeutige Zeitrichtung vorgegeben zu sein; Zeitumkehrinvarianz scheint nicht zu gelten.

Wenn die Vase auf dem Boden zersplittert, geht sie von einem Zustand der geordneten (und gerichteten) Bewegung in einen Zustand erhöhter "Unordnung" über: Die Bruchstücke und die Moleküle in ihnen (und der Boden) nehmen die gesamte vorherige kinetische Energie auf, sie bewegen sich jetzt schneller und ungeordneter als vorher: die innere Energie der Scherben (und des Bodens) und die Unordnung  sind gewachsen. Weil erfahrungsgemäß die Unordnung nie mehr ganz rückgängig gemacht werden kann, sagt man, die anfängliche Energie sei (zwar als innere Energie noch vorhanden, aber) entwertet worden. Die Physiker haben ein Maß für die "Unordnung" gefunden, die so genannte Entropie.

Die Erfahrungstatsache, dass bei makroskopischen Gegenständen wie dem Stein oder der Vase Zeitumkehrinvarianz nicht mehr gegeben ist, wird als 2. Hauptsatz der Wärmelehre formuliert:

Entropie kann bei einem Vorgang höchstens vermehrt, aber nie vernichtet werden. Falls sie bei einem Vorgang unverändert bleibt, so ist dieser tatsächlich umkehrbar (reversibel).

Falls man einem makroskopischen Körper die Entropie, die bei einem bestimmten Vorgang zusätzlich entstanden ist, nicht künstlich entziehen und dann anderswo deponieren kann, kann der Vorgang nicht in umgekehrte Richtung ablaufen (falls das doch ginge, würde der Vorgang "von allein" rückwärts ablaufen). Ein solcher Vorgang kann nur einseitig in Richtung größerer Entropie ablaufen, er ist "irreversibel".

 Spiegelspiele

Klebe zwei Spiegelkacheln längs einer Kante mit Klebstreifen so zusammen, dass beide Spiegel um die Klebekante wie um eine Achse geschwenkt, oder wie ein Buch aufgeklappt werden können. Stelle dann einen Gegenstand zwischen die beiden Spiegel und beobachte, wie viele Bilder des Gegenstands je nach Winkel zwischen den Kacheln entstehen.

Aufgaben:

1. Zwischen zwei parallelen, stromdurchflossenen Leitern besteht eine Kraft. Entscheide, welche Richtung die Kraft hat und entwickle eine Vermutung über das Kraftgesetz.

2. Drei gleiche elektrische Ladungen sitzen auf den Ecken eines gleichseitigen Dreiecks. Entwickle eine Vermutung über den Verlauf der elektrischen Feldlinien.

3. Vor einer unendlich ausgedehnten gut leitenden Metallplatte, die geerdet ist, befindet sich eine punktförmige Ladung. Entwickle eine Vermutung über den Verlauf der elektrischen Feldlinien, die Richtung von Kräften und das Kraftgesetz.