Erhaltungsgröße Energie

Die Lageenergie E_L  an einem Punkt P ist eine Funktion der Höhe h des Punktes über dem Vergleichsniveau; sie hängt nicht davon ab, wie ein Körper zu P gelangte. Man könnte auch sagen, sie ist eine Eigenschaft des Körpers am Punkt P allein. Lässt man den Körper los, verliert er nach und nach seine gesamte Lageenergie, wobei er immer schneller wird. Er wandelt seine Lageenergie nach und nach ganz in eine andere Energieform um, die dann von der Geschwindigkeit abhängt und deshalb kinetische Energie E_kin genannt wird.

In der Mechanik spielen außer der Lageenergie auch Spannenergie und kinetische Energie eine Rolle. Die ersten beiden sind Formen einer potenziellen Energie. Sie sind eine Eigenschaft eines Körpers P an einer bestimmten Position.

Höhe Lagenergie EL h m· g· h doppelte Höhe 2· h doppelte Lageenergie dreifache Höhe 3· h dreifache Lageenergie vierfache Höhe 4· h vierfache Lageenergie

Dehnung s Spannenergie Esp s D/2 · s2 doppelte Dehnung 2· s vierfache Spannenergie 3-fache Dehnung 3· s 9-fache Spannenergie 4-fache Dehnung 4· s 16-fache Spannenergie

Geschwindigkeit kinetische Energie Ekin v m/2 · v2 doppelte  Geschwindigkeit 2· v vierfache kinetische Energie 3-fache  Geschwindigkeit 3· v 9-fache kinetische Energie 4-fache Geschwindigkeit 4· v 16-fache kinetische Energie

Ein Versuch zeigt: Wenn der Körper aus doppelter Höhe fällt, wenn er also anfänglich die doppelte Lageenergie hatte, dann erreicht er nicht etwa die doppelte Geschwindigkeit, sondern nur das Ö2-fache (wurzel 2-fache). Erst bei vierfacher Höhe und vierfacher Lageenergie erreicht er die doppelte Geschwindigkeit mit vierfacher kinetischer Energie.

Wenn der Körper "unten", auf dem Vergleichsniveau, angekommen ist, hat er seine ganze Lageenergie verloren. Stattdessen hat er die Geschwindigkeit v erreicht und besitzt nun die kinetische Energie E_kin = m/2 v²   von gleicher Größe wie die ursprüngliche Lageenergie "oben". Das ist eine Folge der Tatsache, dass in einem abgeschlossenen System die Gesamtenergie konstant ist. Das ist der Energieerhaltungssatz.

Ein abgeschlossenes System ist ein System, das keine Energie nach außen abgibt oder von dort aufnimmt. Es ist also ein System, in dem der Energieerhaltungssatz gilt.

Diese Tatsache kannst du in sehr guter Näherung bei einem Federpendel sehen. Es wechseln sich Zeitpunkte ab, bei denen die Pendelmasse kurzzeitig ruht, und Zeitpunkte bei denen die Pendelmasse mit dem Betrag nach größter Geschwindigkeit durch die Ruhelage hindurchgeht. Beim Durchgang durch die Ruhelage hat die Pendelmasse offenbar größte kinetische Energie. Die ruhende Pendelmasse befindet sich kurzzeitig im oberen oder unteren Umkehrpunkt. Die Feder ist dann maximal gedehnt oder zusammengepresst; sie enthält maximale Spannenergie. Das wiederholt sich und wiederholt sich. Es fasziniert schon das bloße Zuschauen.

Wenn nicht geringe Energieverluste vorhanden wären, die wir außer Acht lassen wollen, würde sich die Schwingung beliebig lange fortsetzen, die Energie würde ständig zwischen kinetischer und Spannenergie wechseln, und an der recht konstant bleibenden Amplitude würden wir erkennen, dass die Gesamtenergie immer (weitgehend) konstant ist.

Mit Hilfe eines Sonarmeters lässt sich die Bewegung auch grafisch auf dem Bildschirm darstellen. Du verstehst hoffentlich den Zusammenhang zwischen der gesehenen Bewegung und ihrer Darstellung durch einen t-x- bzw. t-v-Graphen:

Abb. 1: Schwingung eines Federpendels aufgenommen mit dem Sonarmeter: Betrachte zunächst den t-x-Graphen: Zeitpunkte mit maximaler Auslenkung  (Umkehrpunkte) und maximaler Geschwindigkeit beim Durchgang durch die Ruhelage wechseln sich ab. Abgesehen von Verlusten durch eine kleine Reibung scheint das immer so weiter zu gehen. Der t-v-Graph passt dazu: In den Umkehrpunkten ist die Geschwindigkeit 0. Beim Durchgang durch die Ruhelage hat sie maximalen Betrag. Wenn die Pendelmasse immer bis zum selben oberen bzw. unteren Umkehrpunkt schwingt, heißt das, dass die maximale Spannenergie konstant ist. Wenn die Pendelmasse beim Durchgang durch die Ruhelage immer dieselbe maximale bzw. minimale Geschwindigkeit hat, heißt das, das die maximale kinetische Energie konstant ist. Wenn die Spannenergie maximal ist, ist die kinetische Energie 0 und umgekehrt.

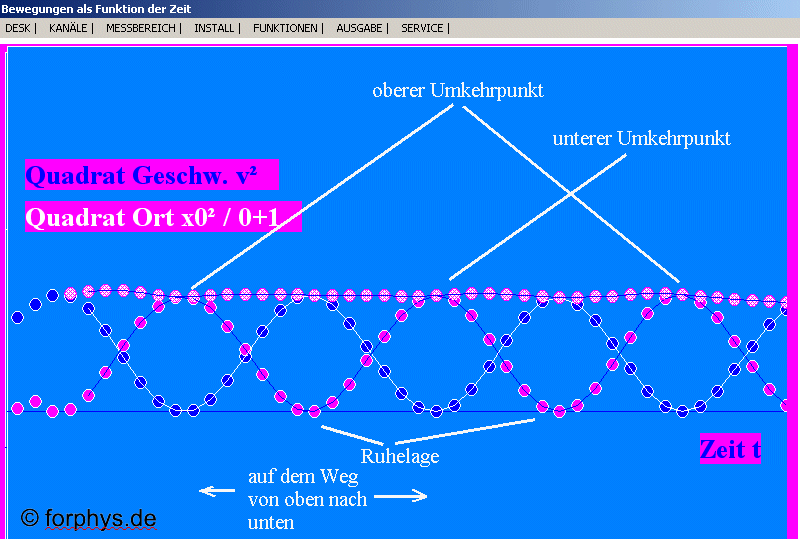Abb. 2: Schwingung eines Federpendels aufgenommen mit dem Sonarmeter: Geschwindigkeit und Auslenkung wurden hier quadriert und mit Faktoren versehen, die D/2 und m/2 entsprechen. Die beiden Kurven mit blauen Punkten und purpurnen Punkten stellen also Ekin und Esp in Abhängigkeit von der Zeit dar. Wenn du die blaue und die purpurne Kurve verfolgst, siehst du, dass sich kinetische und Spann-Energie ständig abwechseln. Das PC-Programm zeichnet auch noch die Summe beider Energien ein. Du siehst im Experiment, dass die Gesamtenergie hervorragend konstant ist: Beim Federpendel gilt der Energieerhaltungssatz in sehr guter Näherung.

Der Energieerhaltungssatz lässt sich nicht allgemein beweisen; aber niemand hat bisher eine Abweichung gefunden. Deswegen wird er als allgemeingültiges physikalisches Prinzip akzeptiert.

Störe dich bitte nicht daran, dass in der Formulierung oben eigentlich ein Zirkelschluss vorliegt: "Der EES gilt in einem abgeschlossenen System, aber das ist auch ein System in dem der EES gilt."  Exakt gilt der EES also, wenn das abgeschlossene System das gesamte Universum ist. Seine Bedeutung liegt darin, dass er in kleineren Systemen, die nicht total abgeschlossen sein können, zumindest in hervorragender Näherung gilt:

Vorhersagen mit dem EES

Mit Hilfe des Energieerhaltungssatzes kann man leicht auf Größe und Gesetzmäßigkeit für andere Energieformen schließen. Üblicherweise geht man dabei immer von einem Dreierschema aus:

I Gesamtenergie "am Anfang"

II Gesamtenergie "am Ende"

III EES

"Am Anfang" heißt "vor der Energieumwandlung", "am Ende" also "nach der Energieumwandlung". Natürlich sind die Beträge beider Gesamtenergien gleich. In der Tabelle geht es also nicht um die Zahlenwerte. Dagegen wirst du die Gesamtenergie am Anfang und am Ende unterschiedlich durch die beteiligten Energieformen mit Hilfe der jeweiligen Gesetzmäßigkeiten ausdrücken. Mit dem EES erhältst du dann eine Gleichung, die du nach der jeweiligen Unbekannten auflösen kannst. Energieverluste z.B. durch Reibung sorgen dafür, dass beide Gesamtenergien nicht gleich sind (wenn man die Verluste nicht mit einbezieht). Wir interessieren uns meistens für Vorgänge, bei denen die Verluste gering sind, so dass der EES (ohne Wärmeabgabe) in guter Näherung gilt.

Beispiel 1

Ein Stein der Masse m soll frei aus einer Höhe h = 5 m fallen mit der Anfangsgeschwindigkeit 0. Luftreibung soll vernachlässigbar sein. Welche Geschwindigkeit v hat der Stein auf halber Höhe?

I Gesamtenergie "am Anfang"	m·g·h
II Gesamtenergie "am Ende"	m·g·h/2 + m/2·v2
III EES	m·g·h = m·g·h/2 + m/2·v2

Von der Gleichung III wird auf beiden Seiten m·g·h/2 subtrahiert mit dem Ergebnis: m·g·h/2 = m/2·v² bzw. v² = g·h . Mit g = 10 m/s² erhältst du v = 7 m/s . Die Aufprallgeschwindigkeit auf dem Boden hätte sich in gleicher Weise zu v' = √2·g·h = √2 ·v = 10 m/s  ergeben. Auf halber Höhe hat der Stein zwar die halbe Energie verloren, aber bereits mehr als die Hälfte der Endgeschwindigkeit erreicht.

Halte dich bitte immer an dieses Dreierschema. Bastelmethoden führen häufig in die Irre!

Ein einfacherer Weg wäre folgender:

Aus der Aufgabenstellung ergibt sich, dass der fallende Stein auf halber Höhe bereits die halbe potenzielle Energie "verloren" hat; sie wurde in kinetische Energie umgewandelt. Der Vergleichspunkt wird auf halbe Höhe gelegt. Beim Start ("oben") hat er im Vergleich zu diesem Punkt die potenzielle Energie m·g·h/2 . Damit:

I Gesamtenergie "am Anfang" (oben)	m·g·h/2
II Gesamtenergie "am Ende" (auf halber Höhe)	m/2·v2
III EES	m·g·h/2  = m/2·v2

Ohne das Schema hätte man gleich sagen können, dass auf halber Höhe die halbe potenzielle Energie in kinetische Energie umgewandelt worden ist. Natürlich folgt das gleiche Ergebnis wie oben.

Beispiel 2

Die harmonische Schwingung eines Federpendels kann gesehen werden als eine ständige Umwandlung von Spannenergie in kinetische Energie und umgekehrt. Zwar gibt es hier auch eine Lageenergie. Sie sorgt sicher dafür, dass sich eine bestimmte Ruhelage einstellt (Position der Pendelmasse, wenn sie ruht). Bezieht man die Spannenergie auf diese neue Ruhelage, ist - wie man zeigen kann - die Lageenergie voll berücksichtigt. Eine weitere Berücksichtigung erübrigt sich.

Die Aufgabe also: Es sei m = 0,1 kg D = 4 N/m = 4 kg/s². Die Pendelmasse werde so angestoßen, dass sie bei einer momentanen Auslenkung x = 0,05 m die Geschwindigkeit v = 1 m/s hat. Welche maximale Auslenkung A (Amplitude) erreicht die Pendelmasse?

I Gesamtenergie "am Anfang"	D/2 ·x2 + m/2·v2
II Gesamtenergie "am Ende"	D/2 ·A2
III EES	D/2 ·x2 + m/2·v2= D/2 ·A2

In Gl. III (EES) wird auf beiden Seiten mit 2/D multipliziert mit dem Ergebnis:    x² + m/D·v² = A² . Also A² = 25·10^-4 m² + 0,1/4 s² · 1 m²/s² = 0,0275 m² . Also A = 0,17 m.

Das Dreierschema sorgt für einen sicher korrekten Ansatz!

Beispiel 3

Eine Kugel rolle reibungsfrei auf einer komplizierten Bahn. Sie startet in der Höhe h = 1,0 m über dem Erdboden, rollt dann ein Stück auf waagrechter Bahn um dann in einen Looping einzutreten. Sie erreicht dabei eine Maximalhöhe von 1,4 m. Sie verlässt den Looping, rollt noch ein Stück waagrecht und rollt dann eine schiefe Ebene hinab. Mit welcher Geschwindigkeit kommt sie unten an?

Es ist offenbar weitgehend gleichgültig, was zwischen Start und Ankunft am Boden passierte. Letzten Endes wird die anfängliche Lageenergie in kinetische Energie umgewandelt. Also:

I Gesamtenergie "am Anfang"	m·g·h
II Gesamtenergie "am Ende"	m/2·v2
III EES	m·g·h = m/2·v2

Es folgt das gleiche Ergebnis wie beim freien Fall: v = √(2·g·h) , ganz gleich, welche Kapriolen die Kugel zwischendurch schlug.

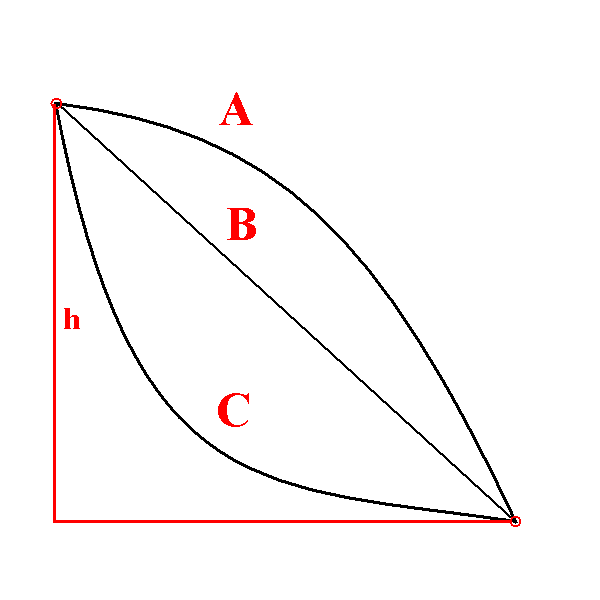Abb. 3: Damit zusammen hängt eine Fangfrage: Die Kugel rolle jetzt aus der Höhe h auf einer von drei möglichen Bahnen hinab (A, B oder C). Auf welchem Weg erreicht die Kugel am schnellsten den Boden? Es ist zu verführerisch: Auf jedem Weg erreicht sie die gleiche Geschwindigkeit! Aber: Auf dem Weg A bleibt die Kugel lange sehr langsam. Erst am Schluss holt sie den Rückstand auf. Für die erste Hälfte der Bahn braucht sie viel Zeit. Kann sie dieses Manko auf der zweiten Hälfte wieder gut machen? Auf welchem Weg wird also die Kugel am schnellsten den Boden erreichen?

Auch "Energieverluste" lassen sich in Rechnung setzen

In der Regel sorgt Reibung dafür, dass Wärme erzeugt wird, die den mechanische Energieformen dann fehlt. Also muss man in der Gesamtenergie auch die abgegebene Wärme unterbringen.

Beispiel 4

Ein Skifahrer wandle 20% (also das 0,2-fache) seiner anfänglichen Lageenergie in Wärme um. Welche Geschwindigkeit hat er 100 m unter seinem Startpunkt? Willkürlich wird dorthin der Nullpunkt der Lageenergie gelegt. h im Folgenden ist also 100 m.

I Gesamtenergie "am Anfang"	m·g·h
II Gesamtenergie "am Ende"	Q + m/2·v2   ( Q = 0,2·m·g·h )
III EES	m·g·h = 0,2·m·g·h + m/2·v2

Was du vielleicht von  Anfang an vermutet hast, bestätigt sich so: 80% der anfänglichen Lageenergie ( 0,8·m·g·h ) steht zur Umwandlung in kinetische Energie zur Verfügung.

Auflösung nach v² liefert:   v²  = 1,6·g·h =>  v  = 40 m/s   . Ohne Reibungsverluste hätte sich ca. 44 m/s ergeben. Q ist die wegen der Reibung abgegebene Wärme.

.

Bilanzcharakter des Energie-Erhaltungssatzes

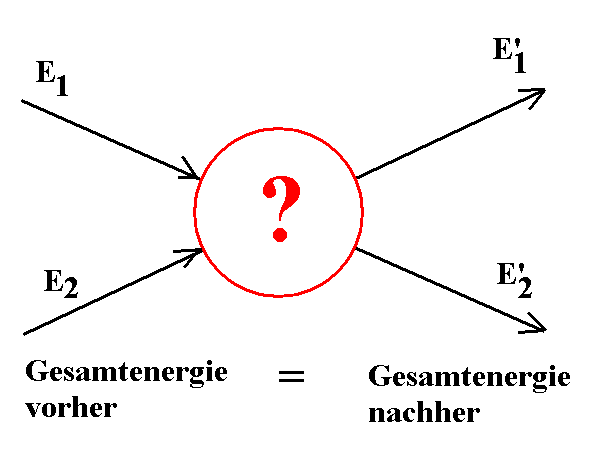Abb. 4: Besonders am Beispiel 3 hast du es sehen können: Es kommt nur auf die Gesamtenergie vor dem eigentlichen Vorgang und der Gesamtenergie nach dem Vorgang an. Der Vorgang selbst, also z.B. das Herabrollen der Kugel, ist belanglos, solange keine Reibungskräfte (genauer: "nichtkonservative Kräfte", was immer das sei) wirken. In der Newtonschen Mechanik hättest du zum gleichen Ergebnis kommen können, aber hättest zu jedem Zeitpunkt die wirkenden Kräfte in Rechnung stellen müssen. Das ist toll: Wenn Energieerhaltung gilt, kommst du mit einem Minimum an Kenntnissen von der Gesamtenergie vor dem Vorgang zu einem Maximum an Kenntnissen nach dem Vorgang. Das meint man mit Bilanzcharakter: Zwei Gesamtenergien werden miteinander verglichen: E1 + E2 = E1' + E2'

Erhaltungssätze führen auf die Gesetzmäßigkeiten für die Energie

Experimenteller Beweis für die Energieformel der Spannenergie Abb. 5: Bei einem Federpendel wird Esp in Ekin umgewandelt, die durch v beim Durchgang durch die Ruhelage gemessen wird. Durch die roten oder gelben Plättchen wird die maximale Dehnung festgelegt. Doppelte (3-fache) Dehnung / Verformung führt zu doppelter (3-fachen) Geschwindigkeit etc., also Esp hängt genauso von s ab wie die kinetische Energie von v. Da v quadratisch in die kinetische Energie eingeht, muss auch s quadratisch in die Spannenergie eingehen. Also:   Aus  Ekin prop. v2   folgt    Esp prop. s2 Kennt man die Größe der kinetischen Energie aus m und v, kennt man auch die Größe der zuvor allein vorhandenen Spannenergie.

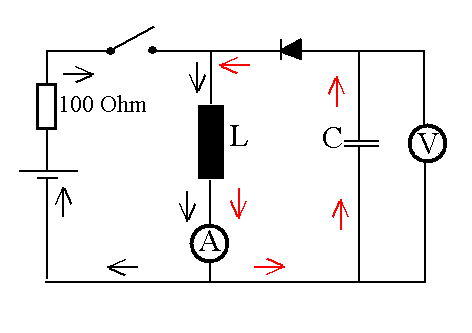
Experimenteller Beweis für die Energieformel der magnetischen Energie im Magnetfeld einer stromdurchflossenen Spule (Prinzipversuch) Abb. 6: Wenn der Schalter geschlossen wird, fließt Strom (schwarze Pfeile) und die Spule enthält magnetische Energie. Wird der Schalter wieder geöffnet, so muss (wegen Induktion) der Strom I unverändert weiter fließen (rote Pfeile). Er lädt dadurch einen Kondensator, dessen elektrische Energie anschließend durch die Spannung U gemessen wird. Es zeigt sich: Doppelte (3-fache) Stromstärke I führt zur doppelten (3-fachen) Ladespannung U, etc. Die magnetische Energie hängt genauso von der Stromstärke I ab, wie die elektrische Energie im Kondensator von dessen Ladespannung U, in beiden Fällen quadratisch. Also:  Aus Eel  prop. U2    folgt      Emag  prop I2.

Beispiel mit elektrischer Energie und innerer Energie

Beispiel 5

Ein Wasserkocher hat eine Leistungsaufnahme von 2000 W. Er ist 1 min = 60 s in Betrieb und heizt 1 Liter Wasser von 20 ⁰C auf. Um diese Wassermenge um 1 ⁰C zu erhitzen sind 4,2 kJ nötig. Um wieviel  steigt die Temperatur?

Energieerhaltung gilt hier, wenn die gesamte Stromarbeit in Wärme umgewandelt wird und diese ganz vom Wasser im Kocher aufgenommen wird. In der Realität wird etwas Wärme auch an die Umgebung abgegeben.

Energieaufnahme aus dem Stromnetz: W = P·t = 2000 J/s · 1 · 60 s = 120 kJ . Das ist 120/4,2 = 28,6 mal mehr als für die Erwärmung von 1 ⁰C benötigt wird. Die Temperatur steigt also um 28,6 ⁰C auf 48,6 ⁰C.

Vgl. auch Impulserhaltungssatz