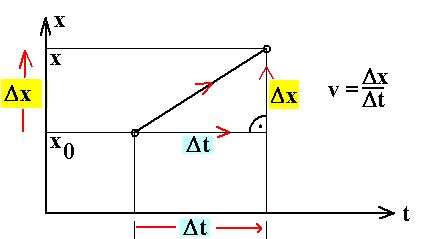
| v = Δx/Δt |
.
Diese Gleichung wird so gelesen: Wenn bei einer solchen Bewegung in einem Zeitabschnitt Δt eine Ortsänderung Δx erfolgt, ist Geschwindigkeit gleich der Ortsänderung Δx pro Zeitabschnitt Δt.
|
. . |
Physik für Schülerinnen und Schüler Geschwindigkeit und Beschleunigung in allgemeinen Fällen © H. Hübel Würzburg 2013 |
Empfohlene Glossarthemen: |
Impres-sum |
|
Geschwindigkeit ist die Steigung des t-x-Diagramms, Beschleunigung die Steigung des t-v-Diagramms. |
 |
Im Fall einer gleichförmigen Bewegung, also einer
kräftefreien Bewegung, ist die Steigung des t-x-Diagramms
konstant, und es gilt also:
. Diese Gleichung wird so gelesen: Wenn bei einer solchen Bewegung in einem Zeitabschnitt Δt eine Ortsänderung Δx erfolgt, ist Geschwindigkeit gleich der Ortsänderung Δx pro Zeitabschnitt Δt. |
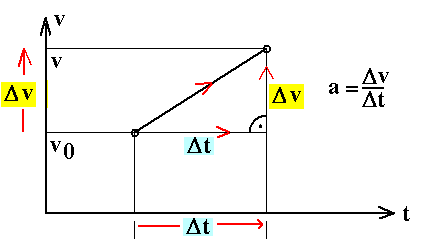 |
Im Fall einer gleichmäßig beschleunigten Bewegung, also
einer Bewegung mit konstanter Kraft, ist die Steigung des
t-v-Diagramms konstant. Dann gilt also
Diese Gleichung wird so gelesen: Wenn bei einer solchen Bewegung in einem Zeitabschnitt Δt eine Geschwindigkeitsänderung Δv erfolgt, ist Beschleunigung a gleich der Geschwindigkeitsänderung Δv pro Zeitabschnitt Δt. |
Die Aussage des ersten Kastens gilt aber auch ganz allgemein. Nur, was bedeutet im allgemeinen die Steigung? Bevor das mathematisch geklärt wird, wird dir hier schon ein vorläufiges anschauliches Verständnis vermittelt.
B "Manueller Steigungsbegriff"
Vielleicht ist es dir noch nicht bewusst geworden, aber nicht nur Texte werden, gemäß der europäischen Tradition, von links nach rechts gelesen, sondern auch Bilder und Graphen, speziell physikalische Graphen. Als Maler noch gegenständlich malten, waren ihre Gemälde vielfach so komponiert, dass der Blick des Betrachters von links nach rechts in das Bild geführt wurde.
Genauso ist es mit einem physikalischen Graphen, z.B. einem t-x-Diagramm. Jeder Betrachter wird dann die Bewegung von links nach rechts, also beginnend mit kleinen Zeiten in Richtung wachsender Zeiten, beschreiben. Dementsprechend wirst du deine Hand in einer ganz bestimmten Weise an den Graphen legen, wenn du seinen Verlauf mit dieser Handhaltung andeuten möchtest.
 |
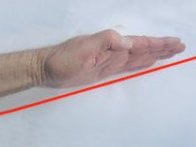 |
Wenn man den Graphen (rot) von links nach rechts durchläuft, steigt er, entsprechend der Handhaltung, an. Dazu gehört eine positive Steigung. Links große positive Steigung, rechts kleinere positive Steigung. |
 |
 |
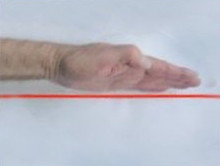
Wenn man den Graphen (rot) von links nach rechts durchläuft,
fällt er, entsprechend der Handhaltung. Dazu gehört eine negative
Steigung. Links sehr kleine (stark negative), rechts nicht
ganz so kleine (mäßig negative) Steigung.
(Beachte: -10 < -5, aber 10 > 5 ) |
 |
Hier ist die Steigung 0.
Wenn der zugehörige Graph ein t-x-Diagramm ist, ist die Steigung gleich der Geschwindigkeit v. An einer solchen Stelle mit Steigung 0 ruht also der Körper (kurzzeitig), ist die Geschwindigkeit 0. Wenn der zugehörige Graph ein t-v-Diagramm ist, ist die Steigung gleich der Beschleunigung a. An einer solchen Stelle ändert sich also die Geschwindigkeit (kurzzeitig) nicht, die Beschleunigung ist 0. |
Wie praktisch dieses anschauliche Verfahren ist, siehst du an folgendem Beispiel
Hier soll zu einem gegebenen t-x-Diagramm zugehörige t-v- und t-a-Diagramme erraten werden. Die Steigung ist dazu sehr hilfreich, sogar in der anschaulichen Variante des "manuellen Steigungsbegriffs".
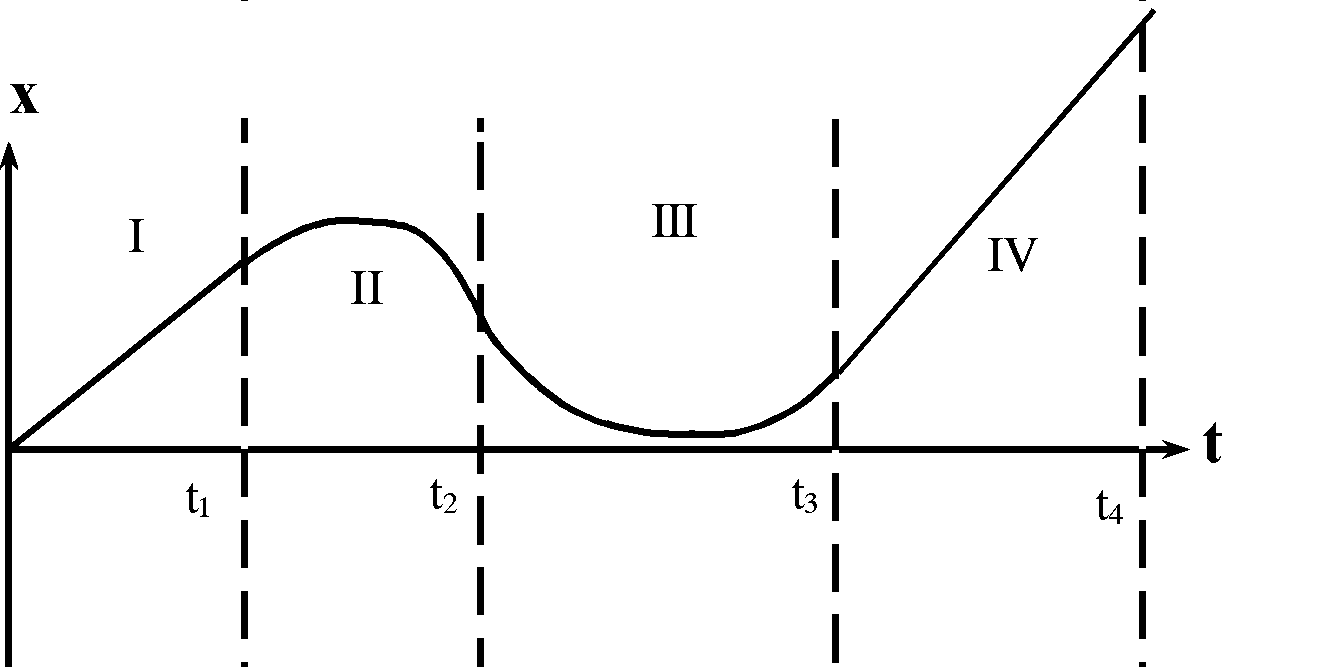 |
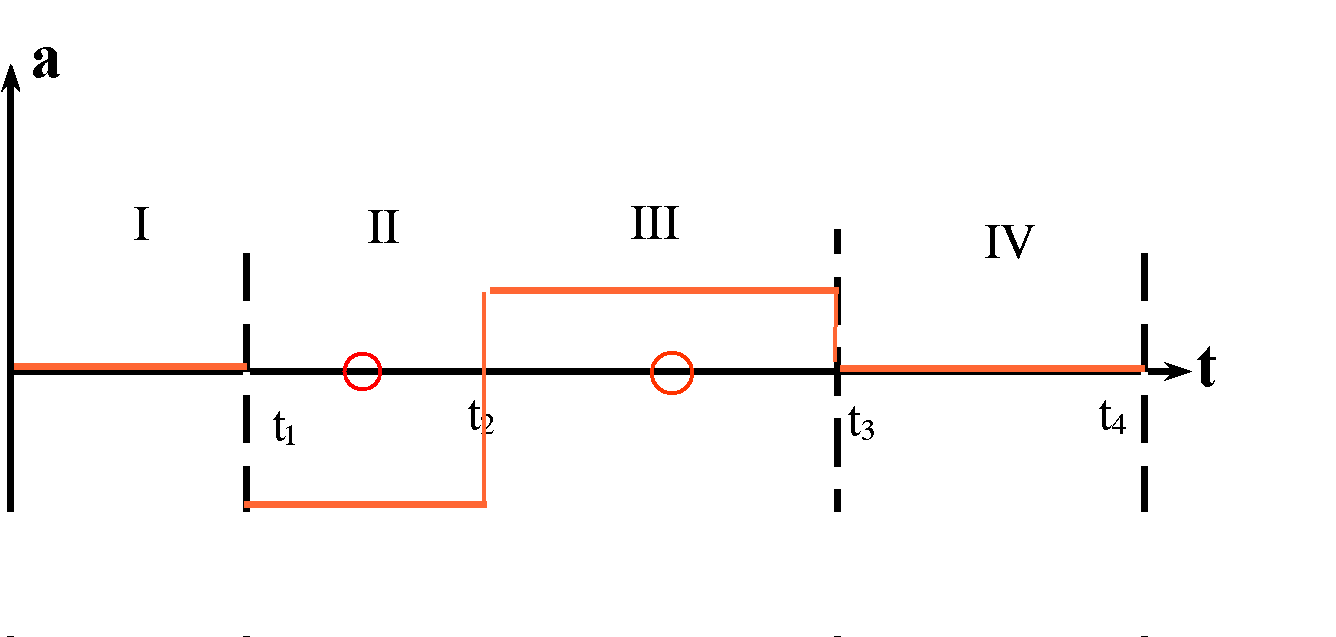
Gegebener t-x-Graph. Es sind hier 4 Bereiche markiert. In den Bereichen I und IV liegt eine gleichförmige Bewegung vor, in den Bereichen II und III eine beschleunigte Bewegung, vielleicht sogar eine gleichmäßig beschleunigte. |
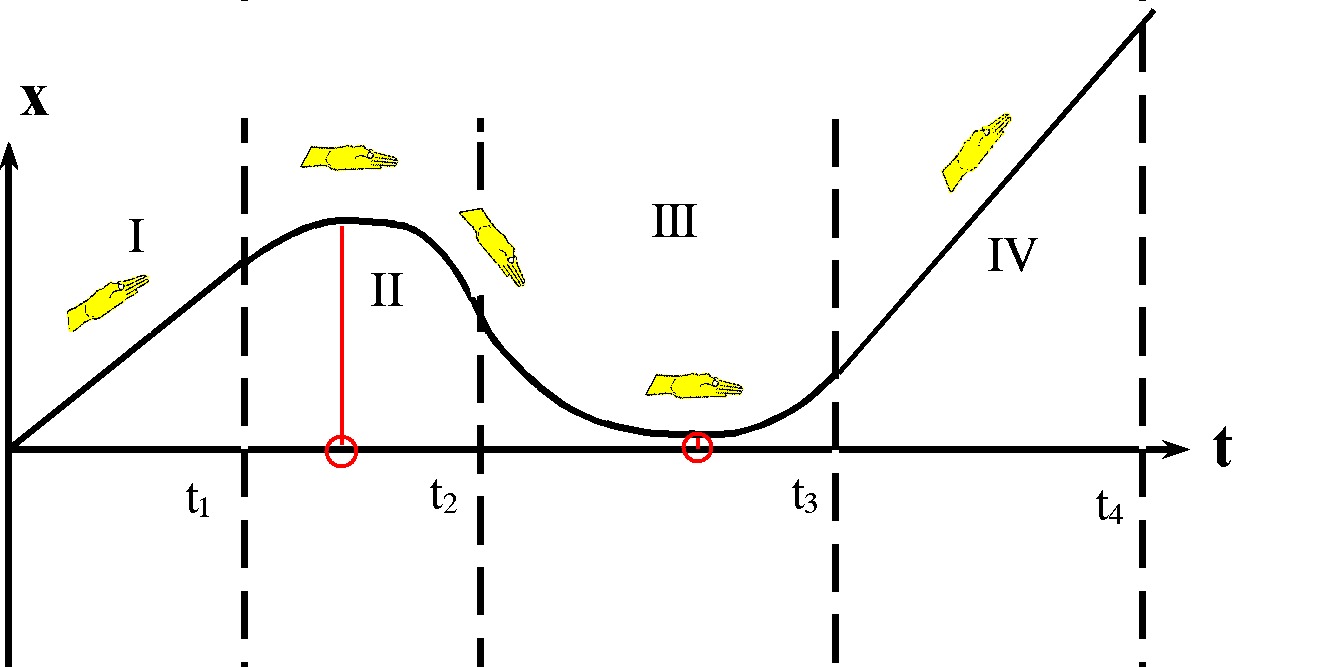 |
Denke dir jeweils die Hand hinzu, die die Steigung des Graphen ( = Geschwindigkeit) anzeigt. Du erkennst sofort Zeiten, zu denen die Steigung bzw. Geschwindigkeit 0 ist (rot markiert), Zeitabschnitte, in denen die Steigung positiv ist, und einen Zeitabschnitt, in dem die Steigung ( = Geschwindigkeit) negativ ist. |
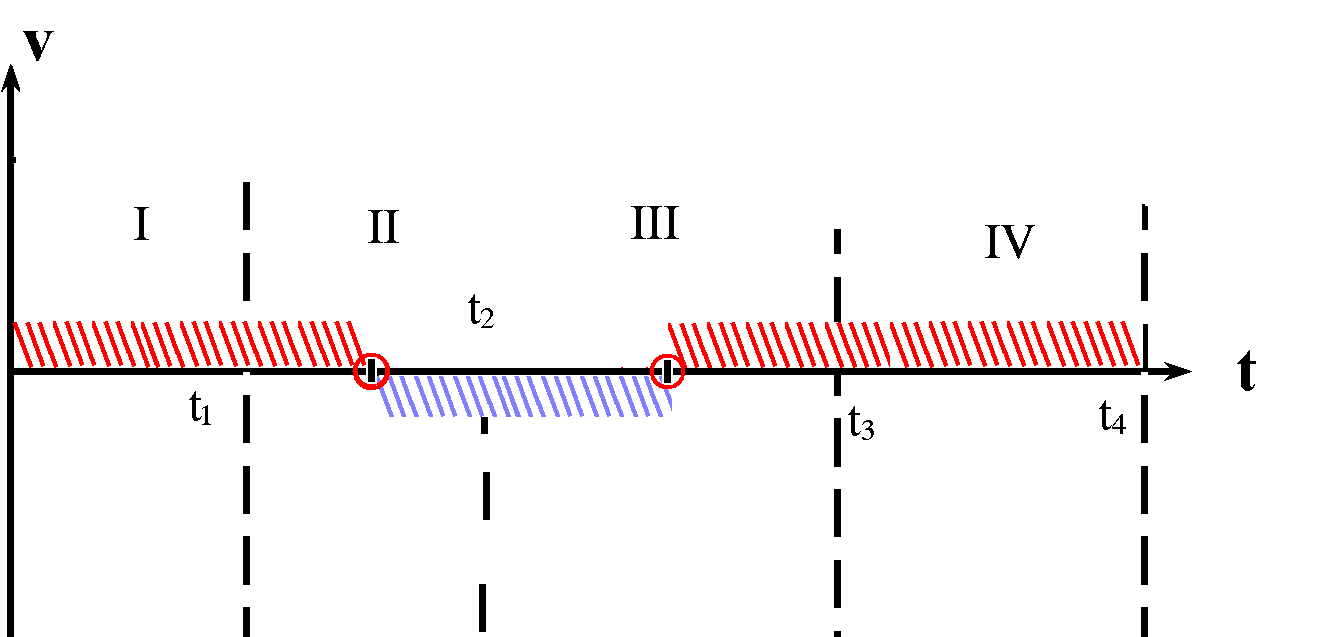 |
Durch Schraffieren trägst du deine Erkenntnisse über das
Vorzeichen der Geschwindigkeit (Steigung) in ein t-v-Diagramm ein.
Soweit ist der t-v-Graph gesichert.
Du erkennst aber auch zwei Bereiche, in denen die Steigung ( = Geschwindigkeit) konstant positiv ist. Du kannst auch einen Zeitpunkt erkennen, bei dem die Steigung dem Betrag nach maximal, aber negativ ist. Wie groß die Steigung jeweils ist, könntest du bestenfalls dann entscheiden, wenn Maßstäbe gegeben wären. Du musst jetzt nur einen Verlauf des t-v-Graphen erraten, der zu den gesicherten Fakten passt. |
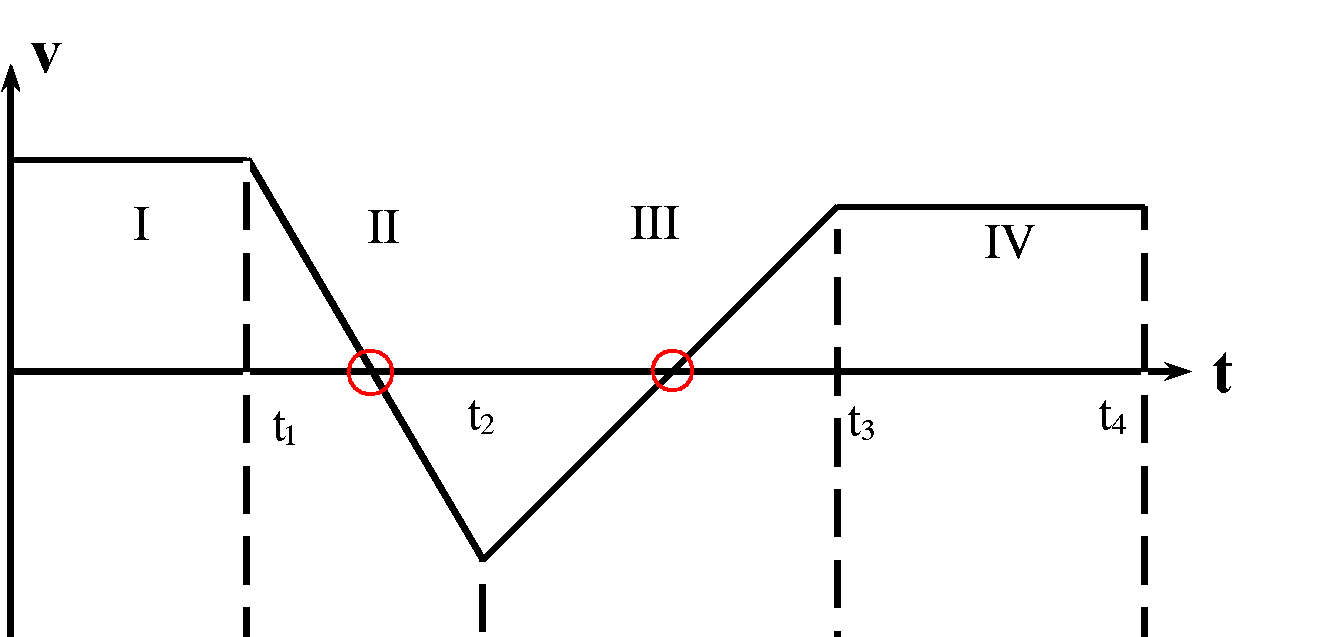 |
Dies könnte ein Ergebnis sein.
An der konstanten Steigung in den Bereichen II und III erkennst du, dass hier wirklich eine gleichmäßig beschleunigte Bewegung vorliegt. (Ohne genauere Angaben zum t-x-Diagramm ist das aber eine reine Vermutung.) |
 |
Genauso kannst du vorgehen, um die jeweiligen Beschleunigungen
zu erraten.
Im Abschnitt II ist die Beschleunigung konstant negativ. Von der Zeit t1 aus wird dabei das Fahrzeug offenbar zuerst bis zum Stillstand abgebremst (roter Kreis), dann wieder schneller. Bei t2 erreicht es seine kleinste (negative) Geschwindigkeit und ist dort gleichzeitig am schnellsten (maximales Tempo; im Vergleich zu benachbarten Zeiten). Ähnlich steigt im Abschnitt III die Geschwindigkeit gleichmäßig an mit konstanter positiver Beschleunigung. Dennoch wird das Fahrzeug zunächst bis zum Stillstand abgebremst (roter Kreis) und dann erneut schneller, bis es bei t3 die größte Geschwindigkeit und das größte Tempo erreicht. |
Die Bezeichnung "manueller Steigungsbegriff" ist nicht offiziell. Wahrscheinlich hat dein Lehrer noch nie etwas von ihr gehört. Das zugehörige Verfahren ist aber sehr nützlich.
D Durchschnittswerte und Momentanwerte für Geschwindigkeit und Beschleunigung
Noch einmal zur Erinnerung das folgende Bild:
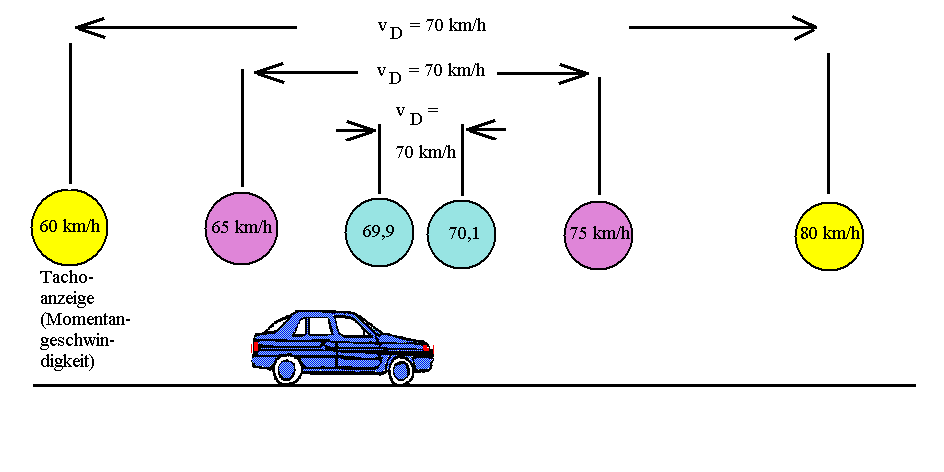 |
| In den Kreisen ist die jeweilige Tachoanzeige eingeblendet. Es handelt sich ganz klar um eine beschleunigte Bewegung. In den verschiedenen Zeitabschnitten - gekennzeichnet durch jeweils gleiche Farbe - ergibt sich immer dieselbe Durchschnittsgeschwindigkeit vD = 70 km/h. Je kürzer das Zeitintervall, desto weniger unterscheidet sich die tatsächliche Geschwindigkeit v, genannt Momentangeschwindigkeit, von der Durchschnittsgeschwindigkeit vD. |
Wenn bei einer beliebigen eindimensionalen Bewegung im Zeitabschnitt Δt eine Ortsänderung Δx erfolgt, dann erhält man - ganz gleich, wie sich die Momentangeschwindigkeit in dem Zeitabschnitt verhält - die Durchschnittsgeschwindigkeit vD durch den Quotienten
| vD = Δx/Δt |
Aber, je kleiner der Zeitabschnitt Δt ist, desto besser stimmt (in der Regel) die Momentangeschwindigkeit v mit der Durchschnittsgeschwindigkeit vD überein.
Ganz entsprechend:
Wenn bei einer beliebigen eindimensionalen Bewegung im Zeitabschnitt Δt eine Geschwindigkeitsänderung Δv erfolgt, dann erhält man - ganz gleich, wie sich die Beschleunigung a in dem Zeitabschnitt verhält - die Durchschnittsbeschleunigung aD durch den Quotienten
| aD = Δv/Δt |
Aber, je kleiner der Zeitabschnitt Δt ist, desto besser stimmt (in der Regel) die Momentan-)Beschleunigung a mit der Durchschnittsbeschleunigung aD überein.
E Hinweis auf den mathematischen Steigungsbegriff
Die physikalischen Überlegungen von Abschnitt B führen zu einer mathematischen Präzisierung, die in deinem Schulbuch höchstwahrscheinlich erläutert ist:
Es werden mit den oben stehenden Überlegungen jeweils die Steigungen definiert. Man nutzt die Erfahrung, dass sich (in der Regel) der Momentanwert dem (relativ uninteressanten) Durchschnittswert um so besser annähert, je kleiner der Zeitabschnitt Δt ist. Mathematisch lässt man dann Δt gegen 0 streben und definiert die Steigung als Grenzwerte (Limes) der jeweiligen Durchschnittswerte für Zeitabschnitt Δt gegen 0:
|
|
. . |
|
Für dieses so definierte v liest man oft auch v = dx/dt (gelesen "de x nach de t") oder eben v = x* (" x Punkt") bzw. für das so definierte a: a = dv/dt (gelesen "de v nach de t") bzw. a = v* ("v Punkt"). (* soll eigentlich ein hochgestellter Punkt sein).
Darüber wirst du höchstwahrscheinlich im Mathematik- und im Physik-Unterricht noch mehr erfahren.
In der Mathematik heißt so etwas "Ableitung nach der Zeit". Im Mathematikunterricht der Oberstufe kommt aber fast immer eine "Ableitung nach x" vor. Sie wird dort mit einem Strich gekennzeichnet (f ' für die Ableitung der Funktion f nach x). Da in der Physik sowohl Ableitungen nach dem Ort x als auch nach der Zeit t vorkommen, muss man letztere anders kennzeichnen: mit einem Punkt (v* ist die Ableitung der Geschwindigkeit nach der Zeit t).