Bemerkungen (2) zum Artikel von M. Rode, „Beugung an zweidimensionalen Gittern als Modell für die Elektronenbeugung“ im MNU journal, 75(4) (2022), 309 - 314

Er benutzt dazu kommentarlos eine Formel, die wie die Formel für Doppelspalt- bzw. Strichgitter-Interferenz in 1. Ordnung aussieht (sin(δ) = λ/d; von mir „Rode-Formel“ genannt), wobei d aber nicht die Gitterkonstante (entsprechend dem Spaltabstand), sondern der Netzebenenabstand sein soll. λ ist die Wellenlänge. Man könnte aus dem Artikel auch herauslesen, dass Rode die „Doppelspalt/Gitter-Variante“ (Zitat) sogar für eine Deutungsmöglichkeit der Elektronenbeugung im Schulexperiment hält. Da ganz klar ist, dass es sich bei der Kreuzgitter-Interferenz nicht um Doppelspalt- bzw. Strichgitter-Interferenz handelt, scheint die Aussage des Artikels auf tönernen Füßen zu stehen. Der verwirrende Sachverhalt soll hier geklärt werden.

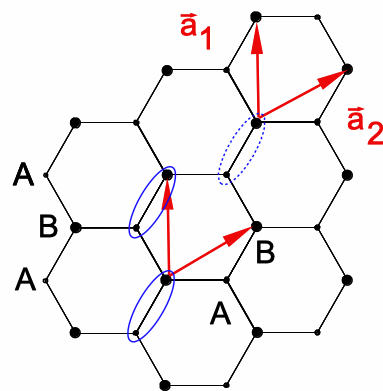
Das betrachtete ebene Gitter ist ein Gitter von mit einander verbundenen Sechsecks-Ringen von Kohlenstoff-Atomen (Trauzettel, 2007), ähnlich einem Graphen-Gitter (Abb. 1).

Abb.1: Graphen-Struktur aus einem dreieckigen Gitter, aufgespannt durch Gittervektoren a1 und a2 mit den Beträgen b1 = 2·d2, wobei jeder Gitterpunkt mit einer Basis aus 2 Atomen belegt ist (Ellipsen).

Es werden dort die Netzebenenabstände, besser „Netzlinienabstände“, d₁ = 213 pm und d₂ = 123 pm = d₁/√3 verwendet. d₁ gehört zur Gitterkonstanten b₁ = 2·d₂ = 246 pm und d₂ zur Gitterkonstanten b₂ = 2·d₁ = b₁·√3 = 426 pm. Die Gitterkonstanten, entsprechend einer Interferenz am Strichgitter, sind jeweils längs der Netzlinien (in Analogie zu Netzebenen bei Raumgittern so genannt) zu messen.

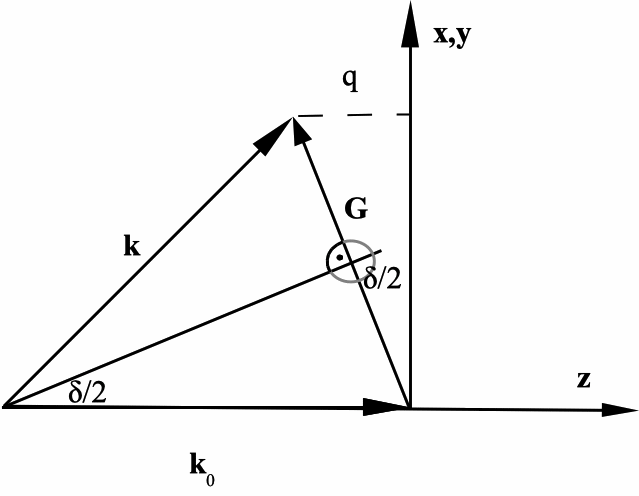
Eine längere Analyse (Hübel, 2023) analog zur Laue-Theorie der Kristallgitter-Interferenz (Kittel, 1968) berechnet für Interferenzmaxima die Wellenzahlvektoren G, die gemäß k = k₀ + G den Wellenzahlvektor k₀ der einfallenden Welle unter Einhaltung der Wellenlänge in den Wellenzahlvektor k der gebeugten Welle überführen (Abb. 2).

Abb. 2: Orientierung der Wellenzahlvektoren k, k0 und des reziproken Gittervektors G. Das Kreuzgitter liegt in der x-y-Ebene. G steht senkrecht auf einem Vektor des realen Gitters in der x-y-Ebene, z.B. auf a1.

Das Ergebnis für den Ablenkungswinkel δ überrascht, da es tatsächlich auch mit der „Rode-Formel“ gewonnen werden kann: sin(δ) = λ/d₁, wobei d₁ ein Netzlinienabstand und nicht eine Gitterkonstante ist, obwohl also die Kreuzgitter-Interferenz wenig mit einer Doppelspalt- bzw. Strichgitter-Interferenz zu tun hat. Der von Rode berechnete Ablenkungswinkel δ ist korrekt und erlaubt dessen weitergehende Entscheidungen bezüglich der Struktur des Streukörpers.

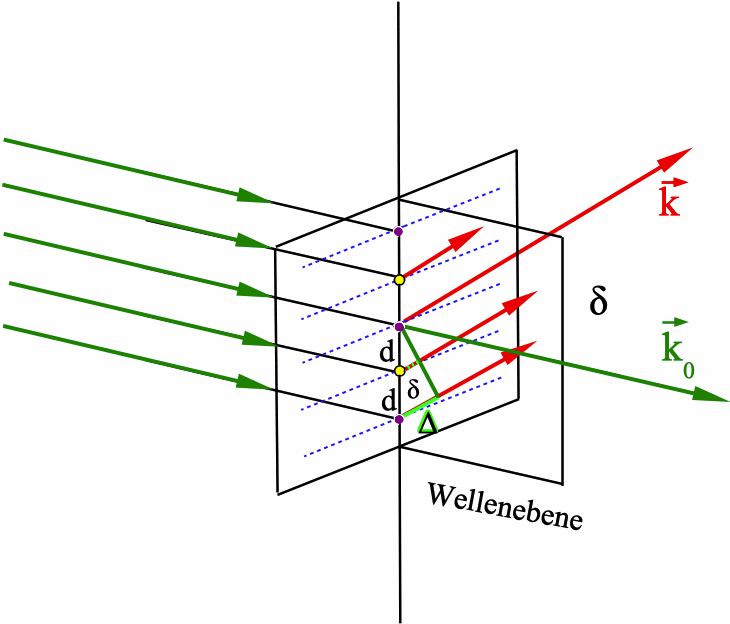
Es soll versucht werden, das folgendermaßen plausibel zu machen mit einer Überlegung, die sich an der schulischen Argumentation für die Bragg-Reflexion orientiert (und ähnliche Schwierigkeiten aufweist): Es wird die Tatsache benutzt, dass der auf das Kreuzgitter senkrecht eintretende Wellenvektor k₀ und der austretende, k, in einer Ebene senkrecht zum Kreuzgitter (Abb. 3), liegen, der Wellenebene. (In der gleichen Ebene liegt auch der zugehörige reziproke Gittervektor G.)

Abb. 3: Bildung von Maxima durch Interferenz „benachbarter“ Strahlen in der „Wellenebene“. Strahlen von parallelen Wellenebenen interferieren unter den gleichen Winkeln.

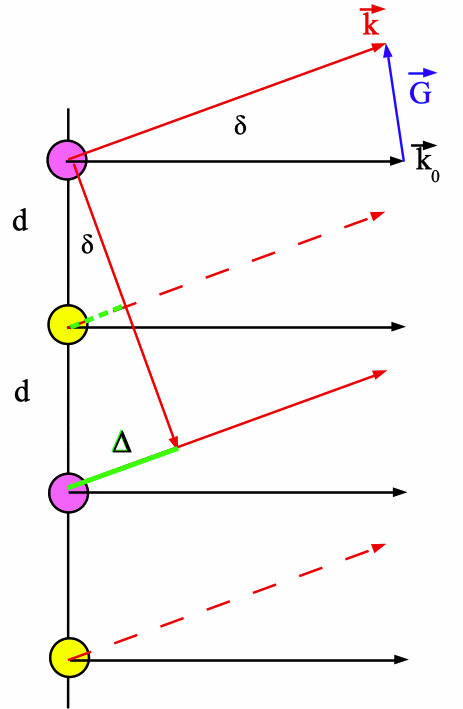
Senkrecht zur Wellenebene und senkrecht zu G - in der Ebene des Kreuzgitters - verlaufen die zugehörigen Netzlinien im Abstand d (für Graphen könnte d = d₁ oder d = d₂ sein). Nach Beugung der Welle an jedem Gitterpunkt in der Wellenebene findet Interferenz statt. Wichtig ist vor allem die von gebeugten Strahlen in der Wellenebene, die parallel zueinander verlaufen. Träfen die einfallenden Wellen in dieser Ebene auf Gitterpunkte (violett und gelb) in direkt aufeinander folgenden Netzlinien im Abstand d (Abb. 4), wäre der Gangunterschied ∆ = d·sin(δ). Dann entstünde ein Maximum, wenn ∆ = n·λ wäre (n ε Z), und wir hätten sin(δ) = n·λ/d, wie bei Rode.

Abb. 4: Interferenz in der Wellenebene. Nur in jeder 2. Netzlinie liegt bei Graphen ein wirksames Streuzentrum (violett gezeichnet). Alle Wellenvektoren liegen in der Wellenebene und „schneiden sich im Unendlichen“.

Die gestreuten, parallelen Wellen überlagern sich „im Unendlichen“ und bilden dort ein Maximum. Das gilt für alle parallelen Wellenebenen und Streuung an allen in ihnen liegenden Streuzentren.

Die Bedingung – Beugung an Streuzentren in einer Wellenebene und in direkt aufeinander folgenden Netzlinien – ist bei dem Graphen-Gitter aber nicht erfüllt: Erst Gitterpunkte (violett) auf Netzlinien im Abstand 2·d haben analoge Lagen und führen zur Interferenz, scheinbar wieder mit dem Gangunterschied ∆ = m·λ (m ε Z). Es folgt: sin(δ) = m·λ/(2·d) (m ε Z) wie bei einem Strichgitter mit der Gitterkonstanten 2·d.

Aber Rode'sche Winkel erhalten wir erstmals mit der Ordnung m = 2. m = 1 führt – wie die Laue-Theorie lehrt - genauso wie alle anderen ungeraden m nicht zu einem der möglichen Vektoren des reziproken Gitters, und damit nicht zu einem erlaubten Ablenkungswinkel. Das kann wohl in der schulischen Herleitung nicht begründet werden; man braucht dazu die obigen Kenntnisse über die möglichen Vektoren des reziproken Gitters. Hätten wir mit dem Impulsübertrag ∆p gearbeitet, könnten wir jetzt auch argumentieren, dass die Ablenkung gemäß m = 1 mit einem Impulsübertrag ∆p verbunden wäre, „den das Kreuzgitter nicht aufnehmen kann“. Setzen wir dagegen n = m/2 (n ε Z) erhalten wir wieder die Rode-Formel, wie bei einem Strichgitter mit der Gitterkonstanten d: sin(δ) = m/2·λ/d = n·λ/d ( n = m/2 ; n ε Z), also die Rode-Formel für beliebige ganzzahlige Ordnung n.

Das Problem mit den evtl. fehlenden Streuzentren in direkt aufeinander folgenden Netzlinien kann entsprechend auch bei der schulischen Herleitung der Bragg-Beziehung auftreten. Beim Kreuzgitter könnte es ebenso - wie es dort in der Schule üblich ist - übergangen werden. Für negative n wurden in Abb. 4 keine Strahlen gezeichnet.

Man könnte das – versuchsweise - auch so auffassen: Die gesamte Netzlinie wirkt jeweils als Streuzentrum. Offenbar spielt es dabei keine Rolle, dass zwei benachbarte (unendlich lange) Netzlinien etwas gegeneinander versetzt sind.

So kann man also dem Autor gut glauben, dass in den Elektronenbeugungsröhren der Lehrmittelfirmen eher Kreuzgitter-Interferenz an ebenen Schichten von Sechsecksringen als Bragg-Reflexion an Raumgittern stattfindet. Dass man deshalb das „Bragg-Verfahren ignorieren sollte“ (Zitat), halte ich für fragwürdig. Denn die Theorie der Kreuzgitter-Interferenz ist m.E. selbst auf schulischem Niveau nicht einfacher als die der Bragg-Reflexion, und es ja auch nicht auszuschließen, dass in anderen Fällen Bragg-Reflexion tatsächlich stattfindet.

Rode kann wohl - nach persönlicher Mitteilung - mit seinem „geschickten Werkzeug“ (Geogebra) den Rode-Winkel δ = 46,3⁰ numerisch für wenige C-Atome in der Sechsecks-Struktur reproduzieren, den er auch für Röntgenstrahlen mit λ = 154 pm gemessen hat.

Literatur

Trauzettel, B. (2007). Von Graphit zu Graphen, Physik Journal 6 (2007), S. 40

Kittel, Ch. (1968). Einführung in die Festkörperphysik, R. Oldenbourg Verlag, München, S. 79

Hübel, H. (2023). Elektronenbeugung am ebenen Kreuzgitter