I.5.1 Fragestellung	Wir hatten schon festgestellt, dass die Natur auf alle Fragen antwortet, die wir in Form eines Experiments an sie stellen. (Siehe Grundfaktum Ib: Messbarkeit aller klassisch denkbaren Eigenschaften) So war es durchaus möglich, beim Doppelspalt einen Durchtrittsort eines Teilchens festzustellen, ebenso wie - in einem anderen Experiment - die Häufigkeit für den Nachweis von Teilchen in der Umgebung einer bestimmten Stelle der Interferenzfigur. Es war aber nicht möglich, für ein bestimmtes Teilchen aus seinem Durchtrittsort abzulesen, ob es in einem Maximum oder nahe einem Minimum die Interferenzfigur erreichen wird. Von welcher Art die Antworten der Natur generell sind, wollen wir jetzt etwas genauer untersuchen. Dazu sollen Experimente mit einzelnen Photonen in einer Anordnung mit einem Polarisator PO und einem Analysator AN dienen. In der Schule können sie in der Regel nicht mit einzelnen Photonen durchgeführt werden, sondern nur mit sehr vielen, also mit normalem Licht. Man muss auf der Ebene des klassischen Lichts bleiben und es dann leider in Kauf nehmen, nach den Lichtversuchen die Ergebnisse mit einzelnen Photonen nur mitzuteilen, es sei denn, man hat geeignete Simulationsprogramme zur Verfügung. Wenn erschwingliche Zähler für einzelne Photonen einmal an Schulen verfügbar wären, könnte sich die Situation ändern.
I.5.2 Polarisationsexperimente mit einzelnen Photonen . . I.5.2.1 Definition der "Polarisation eines Photons" . . 1.5.2.2 Messen einer Eigenschaft eines quantenphysikalischen Systems heißt "einen Messwert be-stimmen" . .	I.5.2.1 Was soll die Polarisation eines Photons sein? Man definiert: Ein Photon, das ein Polarisationsfilter passiert hat, soll die gleiche Polarisation haben wie der elektrische Vektor der zugehörigen Lichtwellen, also wie das verwendete Polarisationsfilter*). Damit ist aber auch klar: Wenn das Photon den Polarisator PO passiert hat, weiß man, welche Polarisation es nach dem Passieren hat. Das Photon könnte durch den Polarisator treten, weil es schon vorher die "richtige" Polarisation gehabt hat. Es könnte aber auch passieren, weil es vorher zwar eine dazu geneigte Polarisation hatte, aber seine evtl. "geringe Chance genutzt hat" (Ingold), trotzdem zu passieren (Vgl I.2.3). Man weiß dann also in keinem Fall, welche Polarisation es vorher hatte. Man sagt, die Polarisation des Photons ist durch den Polarisator be-stimmt worden. Vorher hätte sie sogar un-be-stimmt sein können. Durch die gar nicht dudengemäße Schreibweise soll auf die besondere Bedeutung des Worts "be-stimmt" hingewiesen werden. Damit soll ausgedrückt werden, dass jetzt die Polarisation einen bestimmten Wert hat. Es soll auch darauf hingewiesen werden, dass dieser Wert erst durch die Messung festgesetzt, hergestellt, ..., eben bestimmt worden ist. Und es soll darauf hingewiesen werden, dass jetzt die Polarisation im besprochenen Sinn gemessen, also bestimmt, wurde. 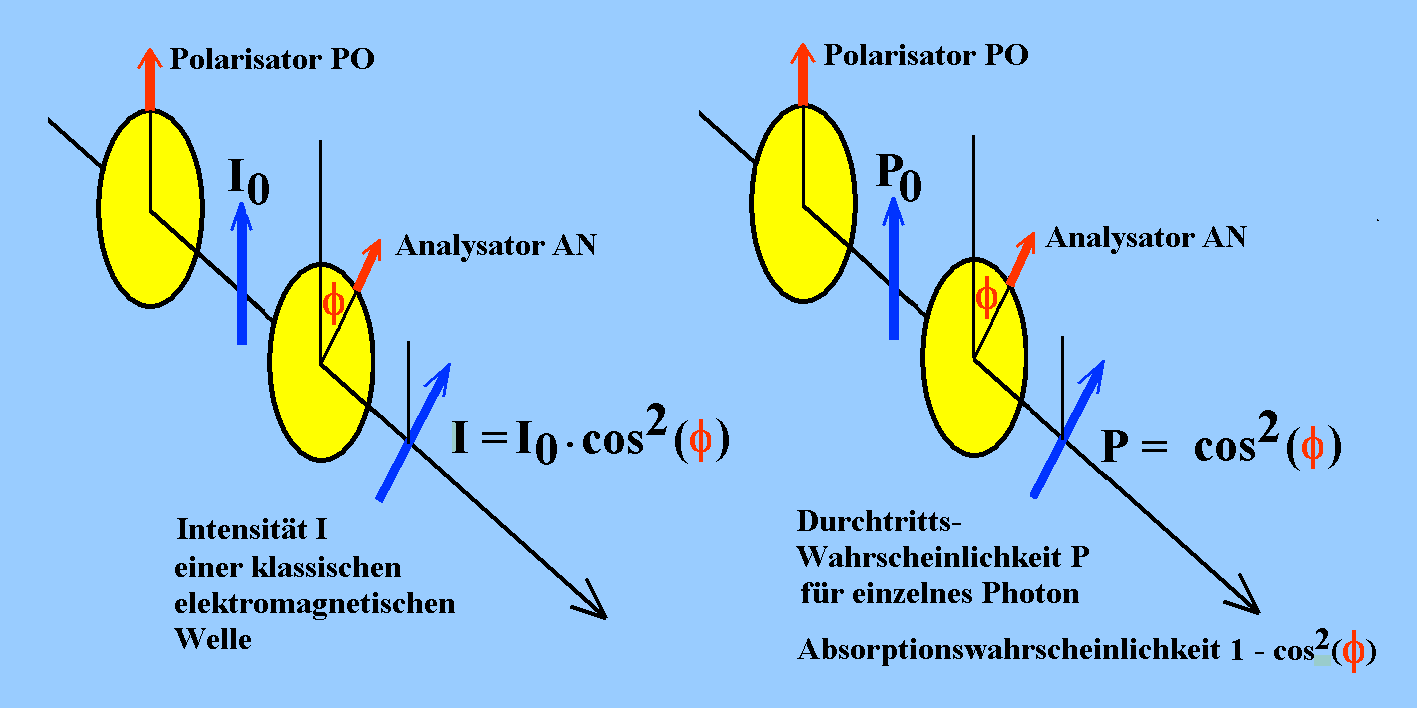1.5.2.2 Bezüglich einer gewählten Polarisationsrichtung kann das Photon be-stimmte Polarisation haben. Dann hat es entweder (nach dem Durchtritt) die gleiche Polarisation wie das Polfilter, erkennbar am Durchtritt durch das Polfilter, oder dazu senkrechte Polarisation, erkennbar an der Tatsache, dass das Photon von einem idealen Polfilter reflektiert oder absorbiert wird, also nicht durchtritt. An einem Polarisator wird die Polarisation eines Photons be-stimmt, be-stimmt im Sinn von eingestellt, hergestellt, festgelegt. Wie auch immer die Polarisation eines Photons vor dem Durchtritt war, nach dem Durchtritt durch ein Polarisationsfilter ist sie gleichgerichtet mit der Polarisationsrichtung des Filters. Ganz Ähnliches gilt für alle klassisch denkbaren Eigenschaften eines quantenphysikalischen Systems. Die zugehörigen Messwerte können durch eine Messung be-stimmt werden. Messen einer Eigenschaft eines quantenphysikalischen Systems heißt "einen Messwert be-stimmen". *) Eine u.U. bessere Definition der Polarisation von Photonen hängt mit der sogenannten Helizität zusammen. Das ist die Spinkomponente in Ausbreitungsrichtung. Bei Photonen stellt es sich heraus, dass die Helizität nur in Bewegungsrichtung oder entgegengesetzt dazu orientiert sein kann. Das hat etwas mit links- und rechtszirkularem Licht zu tun. Zur Spinkomponente +1 gehört rechtszirkulares, zur Spinkomponente -1 linkszirkulares Licht.
I.5.3 Der Messprozess (1) . .Polarisator und Analysator parallel; mit Licht und einzelnen Photonen . .Ein be-stimmter Messwert wird reproduziert. . .Ohne eine Messung hat es keinen Sinn, von Eigenschaften eines Systems zu sprechen. . .Komplementäre Eigenschaften sind nicht gleichzeitig erfüllt/be-stimmt . I.5.3 Der Messprozess (1) . .Polarisator und Analysator parallel; mit Licht und einzelnen Photonen . . . . . . . . I.5.3 Der Messprozess (1) . .Polarisator und Analysator parallel; mit Licht und einzelnen Photonen . . . .	(1) Exp. 1: Polarisator PO und Analysator AN parallel; mit Licht und einzelnen Photonen 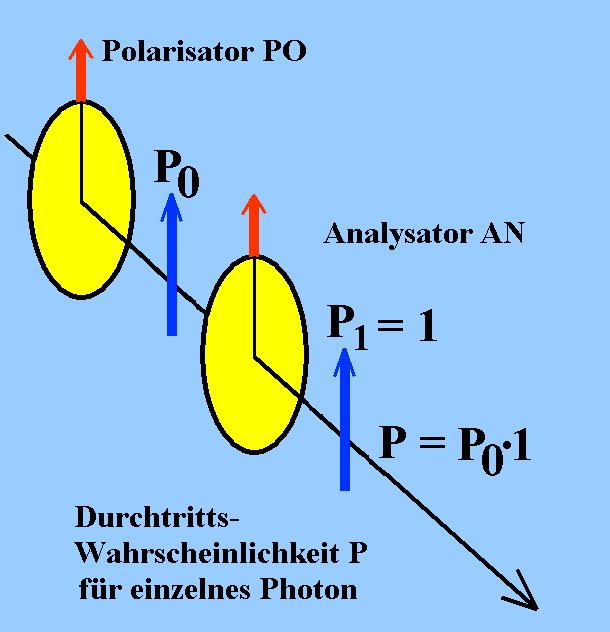Photonen, die den Polarisator PO passiert haben, können stets (bei idealen Polarisatoren) auch den parallel ausgerichteten Analysator AN passieren. Zum Verständnis: (a) Mit Hilfe eines Polarisators und später, eines Analysators, lässt sich die Polarisation des Photons nach dem Durchtritt durch das jeweilige  Polfilter be-stimmen. 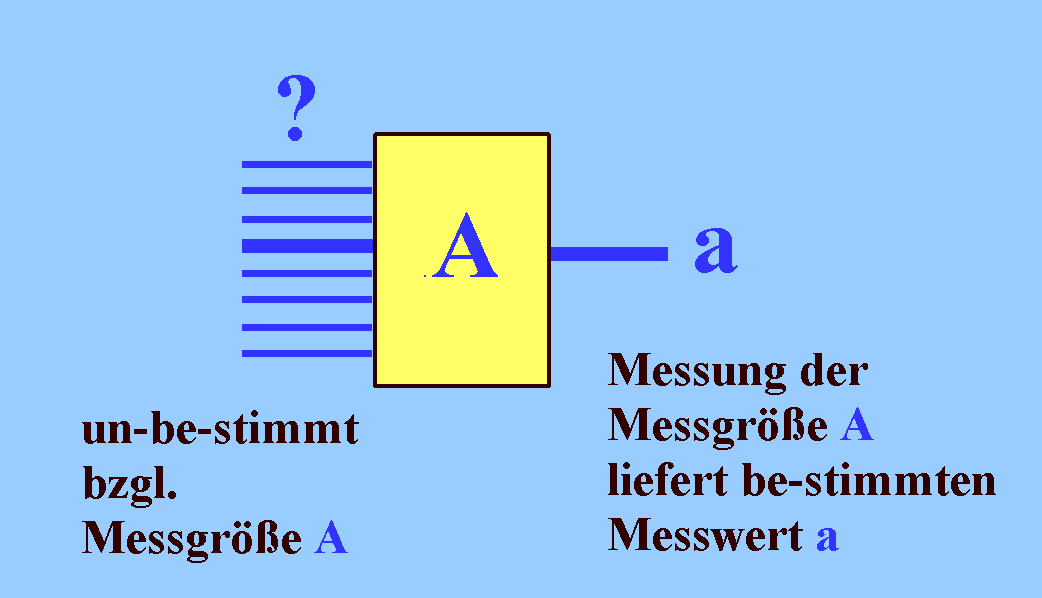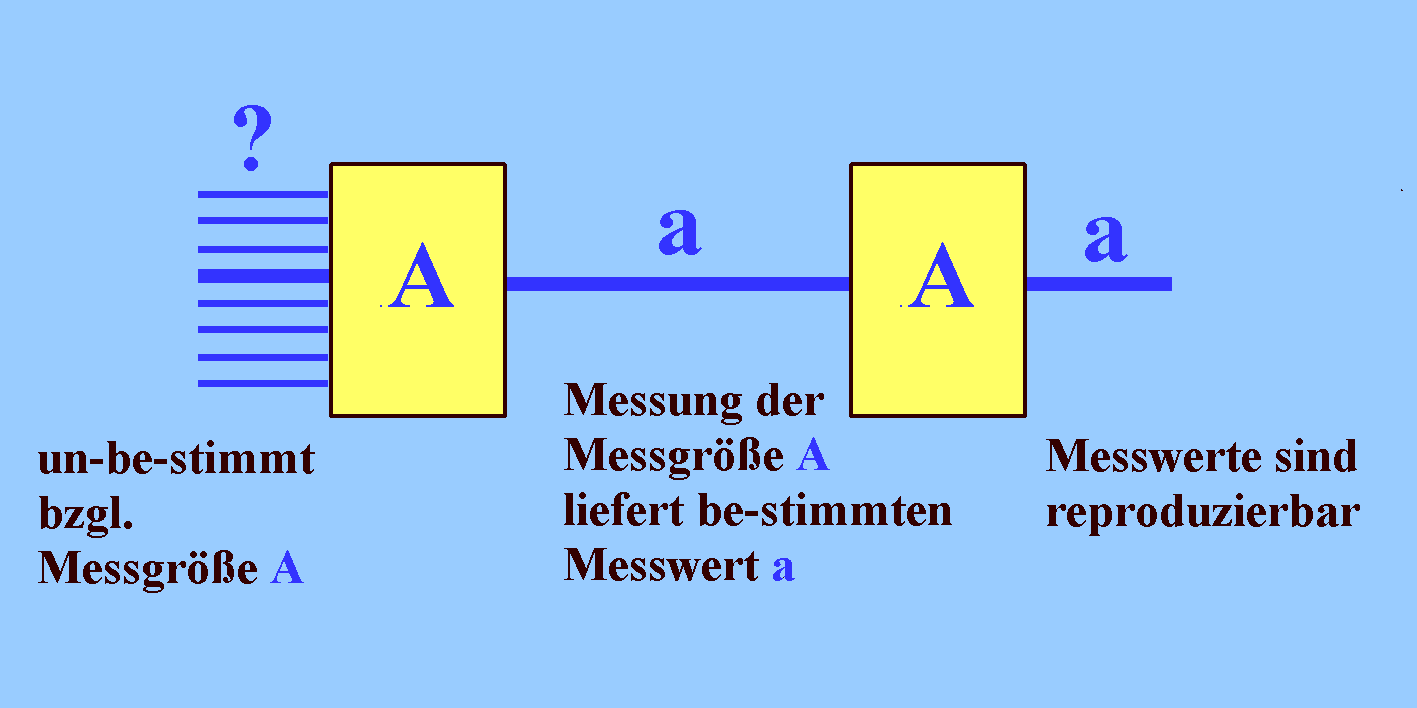(Siehe Grundfaktum IVa: Alle makroskopisch sinnvollen Eigenschaften sind messbar) (b) Eine Messung für eine Messgröße A (hier die Polarisation) liefert immer ein be-stimmtes Ergebnis; das wissen wir bereits. Eine nachfolgende Messung für dieselbe Messgröße liefert das gleiche be-stimmte Ergebnis, wenn sich das System nicht in der Zwischenzeit verändert hat (jeweils mit Licht oder mit einzelnen Teilchen). (Siehe Grundfaktum IVb: "Messergebnisse sind  auch in der Quantenphysik reproduzierbar"). Die Schreibweise "be-stimmt" wird hier angewandt,  damit das Wort nicht mit dem umgangssprachlichen "bestimmt" verwechselt wird. "Be-stimmt" heißt, dass durch die Messung der spezielle Wert der Messgröße "be-stimmt geworden", also sozusagen "hergestellt", "be-stimmt gemacht" worden ist. Der Wert der Messgröße ist dann auch "be-stimmt worden" im Sinn von "gemessen worden". Wenn ein Photon ein Polarisationsfilter passiert hat, hat es die Eigenschaft "be-stimmte Polarisation parallel zum Polfilter". Diese Eigenschaft wird ihm durch nachfolgende gleichartige Messungen nicht mehr genommen (vorausgesetzt, das Photon hat sich in der Zwischenzeit nicht verändert). Nach dem ersten Passieren des Polarisators PO ist ja klar, dass es nicht gleichzeitig die Eigenschaft "be-stimmte Polarisation senkrecht zum Polfilter" hat. (c) Folgerung: Welche Polarisation vor dem ersten Polarisator PO vorlag, ist nach dem Durchtritt durch den Polarisator PO gleichgültig. Sie wirkt sich in keiner Weise aus. Wir können sie auch in keiner Weise feststellen. Wir folgern verschärfend: Vor einer Messung besitzt ein Photon i.A. nicht die Eigenschaft "be-stimmte Polarisation". (Siehe Grundfaktum Id: objektive Un-be-stimmtheit einer Eigenschaft vor einer Messung). Nach Durchgang eines Photons durch ein Polarisationsfilter besitzt es die Polarisationsrichtung des Filters und hat damit be-stimmte Polarisation bzgl. dieser Richtung. Genauso hat auch im allgemeinen Fall ein Quantensystem eine Eigenschaft i.A. nicht, wenn sie nicht gemessen ist. Die Eigenschaft heißt dann objektiv un-be-stimmt. (Siehe Grundfaktum Ia: Nichtexistenz aller klassisch denkbaren Eigenschaften gleichzeitig) Beachten Sie auch hier die gewählte Schreibweise (entgegen der Vorschriften des DUDEN): "be-stimmt" soll immer heißen, dass eine Be-stimmung durch eine Messung vorausging (also eine "Einstellung" des Messwerts) oder dass das System so präpariert wurde, dass eine Messgröße einen festen, scharfen, eben be-stimmten Wert hat. Ohne Bindestrich geschrieben hat das Wort hier immer die umgangssprachliche Bedeutung.
I.5.4 Einschub /E/2 als Maß für die Wahrscheinlichkeit, ein Photon in der Umgebung einer Stelle nachzuweisen	Einschub: Dem Doppelspalt-Versuch und anderen Versuchen mit Licht bzw. der Theorie entnimmt man für die Energiedichte  ρ grob: ρ prop. E2 + B2 .  ρ  ist die klassische Energiedichte in der Umgebung einer Stelle und damit auch proportional zur Wahrscheinlichkeit, dort ein Photon zu finden. (E ist dabei die elektrische Feldstärke der elektromagnetischen Welle und B ihre magnetische Flussdichte. In die Wahrscheinlichkeitsdichte für den Nachweis eines Photons selbst geht außer ρ noch die Photonenenergie ein.) Experimente und Theorie zeigen, dass das Ergebnis aus klassischen Überlegungen in den uns betreffenden Fällen im Wesentlichen richtig bleibt, wenn man E bzw. /E/2 quantentheoretisch richtig behandelt. Das soll hier nicht weiter ausgeführt werden.*)   Das ist für viele Experimente auch mit einzelnen Photonen oft eine große Hilfe, weil dann oft Versuchsergebnisse durch klassische Überlegungen vorhergesagt werden können. *) In Ausdrücken wie E2 bzw.  /E/2 (statt /E/2  eigentlich E*. E) müsste E  als Operator  behandelt und Erwartungswerte bzgl. Zuständen, z.B. mit 1 Photon, berechnet werden. Physiker überlegen sich, dass dann auch "Nichtdiagonal-Elemente" von E eine Rolle spielen können, was wichtig ist für Versuche mit einzelnen Photonen. Ähnliches gilt für B. Beide Felder stehen hier als Ausdruck für das Vektorpotential A, das eigentlich eingeht. Darauf soll hier nicht eingegangen werden.
I.5.5 Der Messprozess (2) . . Polfilter-Kombinationen mit gegeneinander geneigten Polarisatoren bei einzelnen Photonen . Messen einer Eigenschaft eines quantenphysikalischen Systems heißt "einen Messwert be-stimmen" . Komplementäre Eigenschaften sind nicht gleichzeitig erfüllt und damit auch nicht gleichzeitig messbar . . I.5.5 Der Messprozess (2) . . Polfilter-Kombinationen mit gegeneinander geneigten Polarisatoren bei einzelnen Photonen . . . . I.5.5 Der Messprozess (2) . . Polfilter-Kombinationen mit gegeneinander geneigten Polarisatoren bei einzelnen Photonen . .	(2) Exp. 2: Verwendet man einen Analysator AN, der gegenüber dem Polarisator PO um einen Winkel φ um die optische Achse geneigt /gedreht ist, so würde man vielleicht erwarten, dass ein Photon, das erst den Polarisator PO passiert hat, vom Analysator AN gesperrt wird, weil es - jedenfalls nach einer klassischen Vorstellung - die "falsche" Polarisation hat. Es hatte ja auf jeden Fall nach dem Durchtritt durch den Polarisator PO eine bzgl. ihm be-stimmte Polarisation. Stattdessen beobachtet man bei einzelnen Photonen mit der Polarisation des Polarisators PO: Manche Photonen werden vom Analysator AN gesperrt, andere gehen durch. Das ist wieder ein ganz zufälliger Vorgang, der darauf hinweist, dass die Photonen die Eigenschaft "polarisiert wie der Analysator AN" vor ihrem Durchtritt nicht besitzen. Die Wahrscheinlichkeit, mit der solche Photonen den Analysator passieren, hängt vom Winkel φ ab: Bei φ = 0 passieren bei einem idealen Analysator alle Photonen, bei φ = 900 ist die Wahrscheinlichkeit für das Passieren 0, bei φ = 450 ist die Wahrscheinlichkeit gerade 1/2. In jedem Fall ist es so, dass die durchgelassenen Photonen dann (uneingeschränkt) die Polarisation des Analysators AN haben. Man könnte versuchen zu argumentieren, dass das passierende Photon schon vorher die be-stimmte Polarisation des geneigten Analysators AN haben musste, damit es passieren konnte. Andererseits hatte das Photon durch den Polarisator PO gerade eine andere be-stimmte Polarisation, eben die des Polarisators PO, erhalten. Beides kann nicht gleichzeitig richtig sein. Es ergeben sich die Folgerungen: (a) Das durchtretende Photon hat durch den Analysator eine neue be-stimmte Polarisation erhalten. Zuvor hatte es be-stimmte Polarisation bzgl. des Polarisators PO und un-be-stimmte bzgl. des Analysators AN. Nach dem Durchtritt durch den geneigten Analysator AN ist die Polarisation bzgl. des Polarisators PO völlig vergessen worden. Die Photonen, die passieren, haben die be-stimmte Polarisation des Analysators AN (und un-be-stimmte bzgl. des Polarisators PO). Die Photonen, die nicht passieren konnten, haben be-stimmte Polarisation senkrecht zum Analysator (erhalten). Durchtretende Photonen hätten vorher jede beliebige Polarisation bzgl. des Polarisators PO haben können; sie sind also un-be-stimmt bzgl. seiner Polarisationsrichtung PO. (b) Der Zustand eines Teilchens, in dem eine Messgröße A be-stimmt ist (hier: die Polarisation bzgl. des Polarisators PO), kann un-be-stimmt sein bzgl. einer anderen, C, hier also der Polarisation bzgl. des Analysators AN. Genauso ist nach dem Durchtritt durch den Analysator AN die Messgröße Polarisation bzgl. des Analysators AN be-stimmt und bzgl. des Polarisators PO un-be-stimmt. Solche Paare von Messgrößen heißen zueinander komplementäre Messgrößen. Ein Quantensystem kann komplementäre Messgrößen nicht zugleich als Eigenschaften haben. Man hat in Experimenten (und auch in der Theorie) ganze Listen von komplementären Messgrößen aufstellen können, bei denen dieses Phänomen eintritt. Wenn eine Messgröße A be-stimmt ist, ist sie bzgl. einer komplementären Messgröße C un-be-stimmt. Einige Beispiele aus der Liste zueinander komplementärer Messgrößen:          . Komplementäre Größen Ortskoordinate x zugehörige Geschwindigkeits- bzw. (Impuls-)Koordinate  vx (bzw. px) y py (bzw. vy) Amplitude einer elektromagnetischen Welle Phase einer elektromagnetischen Welle; vgl. Kohärente Zustände Ex By Impulskoordinate Drehimpulskoordinate unterschiedliche Drehimpulskoordinaten, z.B. Sx und Sy Drehwinkel φ Drehimpuls J in Bahnbewegung bei einer Kreisbahn eines Teilchens (Drehimpulskomponente senkrecht zur Bahnebene) beim H-Atom:  Gesamtenergie E Ekin bzw.  Epot WWI Interferenzfigur Komplementäre Messgrößen  sind   nicht gleichzeitig messbar Man kann sehr wohl die Polarisation des Photons bzgl. des Polarisators PO messen. Misst man dann noch die Polarisation bzgl. des Analysators AN, was gut möglich ist,  hat das Ergebnis der vorherigen Messung keinen Sinn mehr: Das Photon besitzt nicht mehr die vorher gemessene Eigenschaft (PO). Man sagt, Quantensysteme besitzen nicht alle klassisch denkbaren Eigenschaften gleichzeitig, insbesondere können sie komplementäre Messgrößen nicht gleichzeitig als Eigenschaften haben. Bemerkenswert ist, dass auch die Teilchenzahl eines Quantensystems nicht in jedem Fall Eigenschaft des Systems sein muss. Der Experimentator hat es offenbar in der Hand, welche Eigenschaften des Quantensystems er studieren möchte. Indem er unterschiedliche experimentelle Anordnungen wählt (Polarisator PO oder Analysator AN), erhält er Informationen zu komplementären Eigenschaften (hier entweder die Polarisation des Photons bzgl. des Polarisators PO oder bzgl. des Analysators AN). Es hängt von der Willkür des Experimentators ab – von seiner Fragestellung -, ob sich das Quantensystem mit der einen Eigenschaft (z.B. PO) oder der dazu komplementären Eigenschaft (z.B. AN) zeigt. (Siehe Grundfaktum Ia: Nichtexistenz aller klassisch denkbaren Eigenschaften gleichzeitig)
I.5.6 Der Messprozess (3) . .. .   . . .. .   . . . . .  . . I.5.6 Der Messprozess (3) . .   . . .   . . . . . . . I.5.6 Der Messprozess (3) . .   .. .   . . . . . .  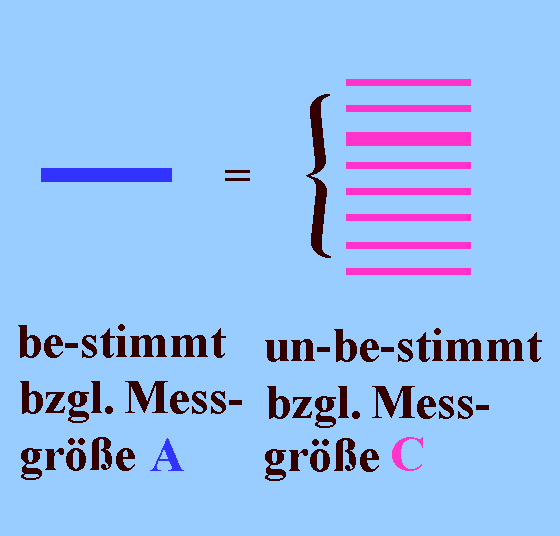 . . . . .	(3) Dies erläutert den Begriff der Un-be-stimmtheit: Ein Zustand eines Teilchens, in dem eine Messgröße A be-stimmt ist, kann zugleich un-be-stimmt sein bzgl. einer anderen dazu komplementären Messgröße C. Wenn die Messgröße A be-stimmt ist, heißt das, dass aufeinander folgende Messungen der Messgröße A immer dasselbe Ergebnis (z.B. a) liefern, wenn keine Änderung des Zustands eintritt. Wenn die Messgröße C un-be-stimmt ist (weil sie keine Eigenschaft des Systems im betrachteten Zustand ist), hat das zur Folge, dass aufeinander folgende Messungen von C streuende Messwerte c liefern. Eine einzelne dieser Messungen für C liefert aber einen be-stimmten Messwert c, z.B. den in das nachfolgende Schema eingetragenen. 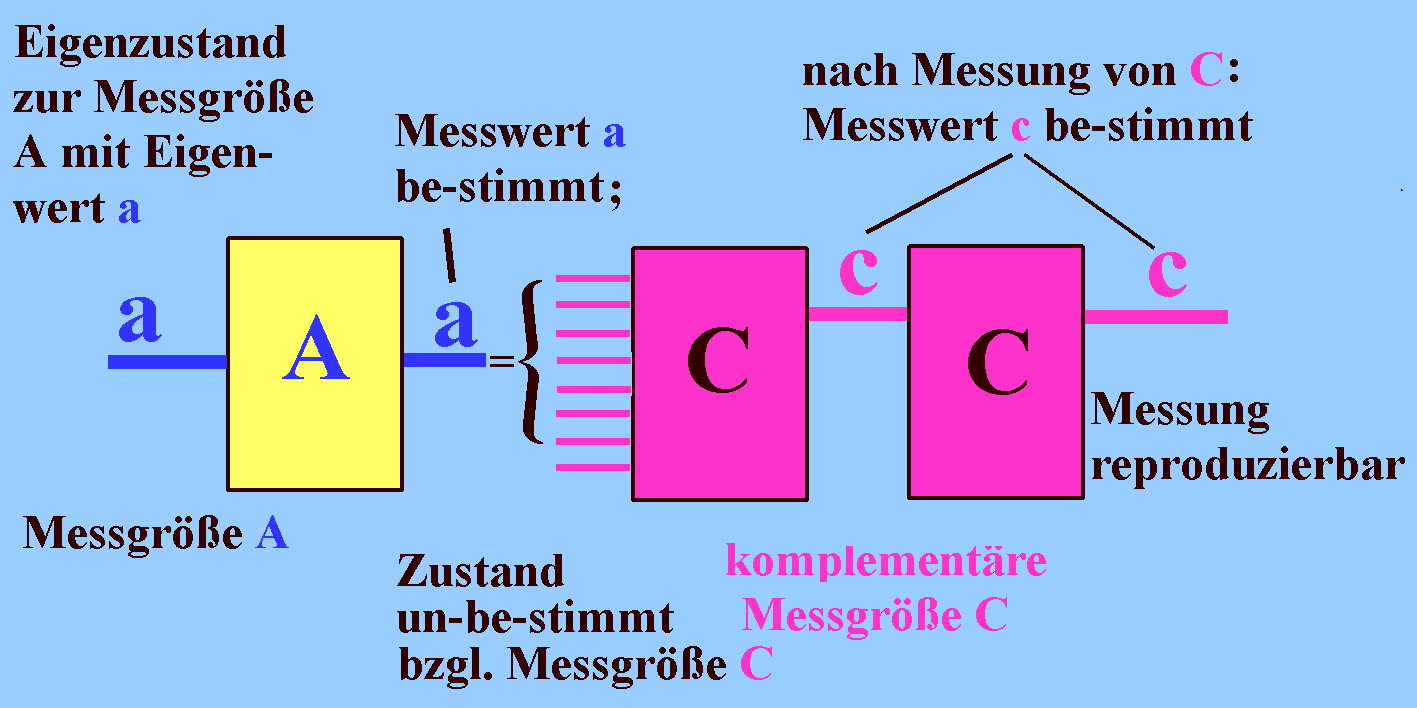Obwohl der Ausgangszustand be-stimmt ist bzgl. Messgröße A und un-be-stimmt bzgl. der komplementären Messgröße C, entsteht nach der C-Messung ein reproduzierbarer Messwert c. 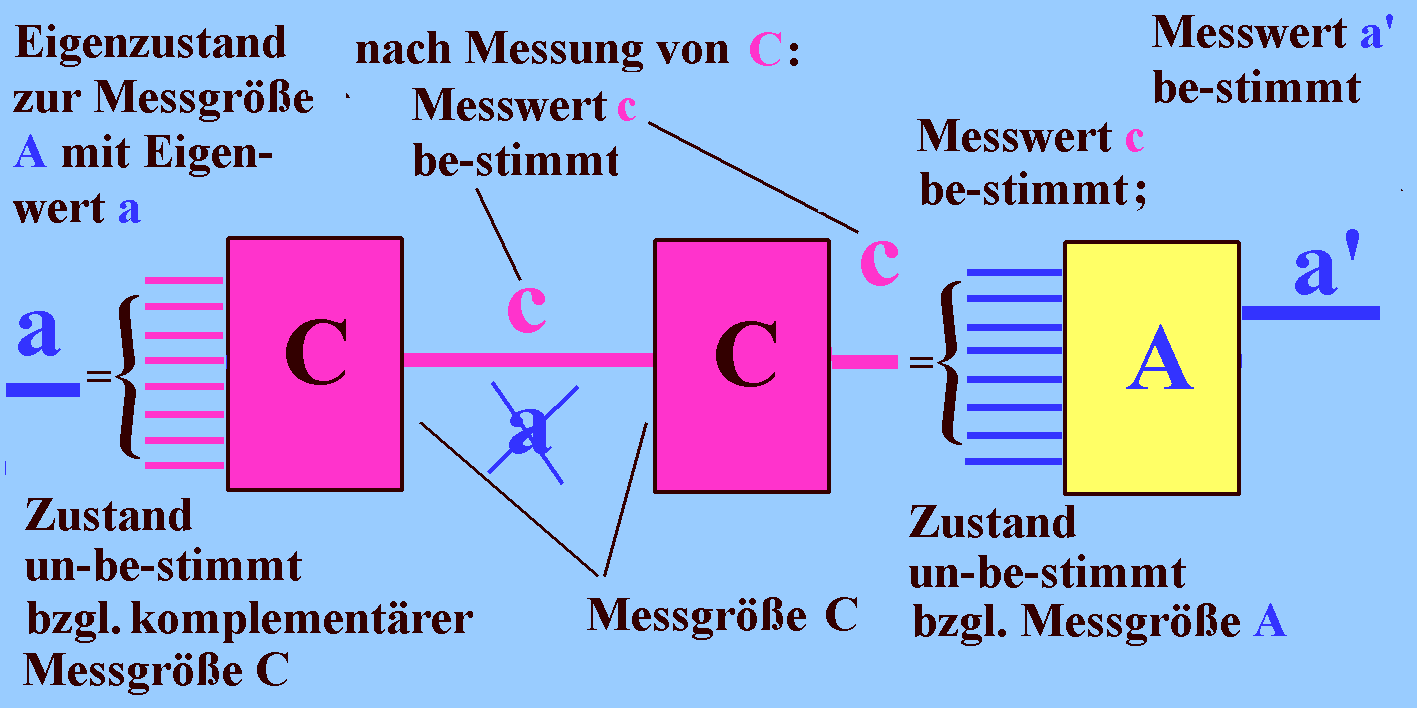Der Ausgangszustand sei be-stimmt bzgl. Messgröße A und un-be-stimmt bzgl. der komplementären Messgröße C. Nach der Messung von C ist der Eigenwert a völlig vergessen worden (ungültig geworden); das System besitzt nicht mehr die Eigenschaft a. Eine erneute Messung von A liefert deshalb i.A. einen völlig anderen Wert a'. Damit ist klargestellt, dass eine Messung einen unvermeidbaren Eingriff in ein Quantensystem darstellt, indem es eine Messgröße be-stimmt macht, die evtl. vorher nicht be-stimmt war, bzw. umgekehrt, dass er eine Messgröße un-be-stimmt macht, die vorher be-stimmt war. (Siehe Grundfaktum IVd: Überlagerungsprinzip) (4) Vor einer Messung besitzt ein Photon i.A. nicht die Eigenschaft "be-stimmte Polarisation". Diese Eigenschaft entsteht i.A. erst durch den Messvorgang. (Ähnlich entsteht der Ort eines Teilchens oder sein Impuls i.A. erst bei einer Messung. Vor der Messung sind Ort und Impuls i.A. un-be-stimmt: Man kann nur eine Wahrscheinlichkeitsverteilung angeben dafür, welche Meßgrößen häufiger oder seltener eintreten werden. Erst, wenn die Messung des Orts vollzogen worden ist, ist ein wohldefinierter (be-stimmter) Ort entstanden, vornehmlich einer, für den die Wahrscheinlichkeitverteilung große Wahrscheinlichkeit vorhergesagt hat. Entsprechendes gilt für eine Messung des Impulses.) (Siehe Grundfaktum Id: objektive Un-be-stimmtheit ) (5) So stellt eine Messung einen in der Regel unvermeidbaren Eingriff in ein quantenphysikalisches System dar, indem eine un-be-stimmte Messgröße in eine be-stimmte überführt wird, wobei in der Regel andere Messgrößen wieder un-be-stimmt werden. Nur in Ausnahmesituationen erfolgt kein Eingriff durch die Messung: Wenn ein System bereits be-stimmt ist bezüglich der fraglichen Messgröße, bleibt es unverändert bei einer zweiten Messung derselben Messgröße, so wie ein Photon, das durch den Polarisator PO getreten ist (Polarisation parallel dazu) auch durch einen Analysator AN tritt, wenn dieser parallel zum Polarisator PO ausgerichtet ist. Das gilt, solange das System zwischen den beiden Messungen nicht verändert worden ist. Um nach dem Durchtritt durch den Polarisator PO die Polarisation bzgl. einer geneigten Richtung zu messen, muss man einen Analysator AN einbauen oder einen ursprünglich parallelen verdrehen, eine deutliche Änderung der Versuchsanordnung. Um den Durchtrittsort beim Doppelspalt zu messen, muss man Detektoren in der Nähe  der beiden Spaltöffnungen aufstellen, man braucht man eine andere Versuchsanordnung, als wenn man die Interferenzfigur ausmessen möchte. Der Wechsel von der einen zu der anderen Anordnung  ist ein ganz radikaler "Eingriff "  in ein quantenphysikalisches System. Allgemein erfordert die Messung der einen Größe (also z.B. des Durchtrittsorts) eine andere experimentelle Anordnung als die Messung einer dazu komplementären Größe (z.B. der Häufigkeitskeitsverteilung innerhalb der Interferenzfigur), ein weiterer Grund, weshalb man aus dem einen Messergebnis nichts für ein dazu komplementäres lernen kann. (6) Polfilter-Beobachtungen sind zudem klassisch deutbar: Das Betragsquadrat der Welle hat etwas mit der Nachweiswahrscheinlichkeit zu tun; der Vergleich mit dem Experiment bestätigt umgekehrt, dass das modellmäßige Denken in "elektromagnetischen Wellen" gemäß I.5.4 oder I.2.3  manchmal ganz nützlich ist. 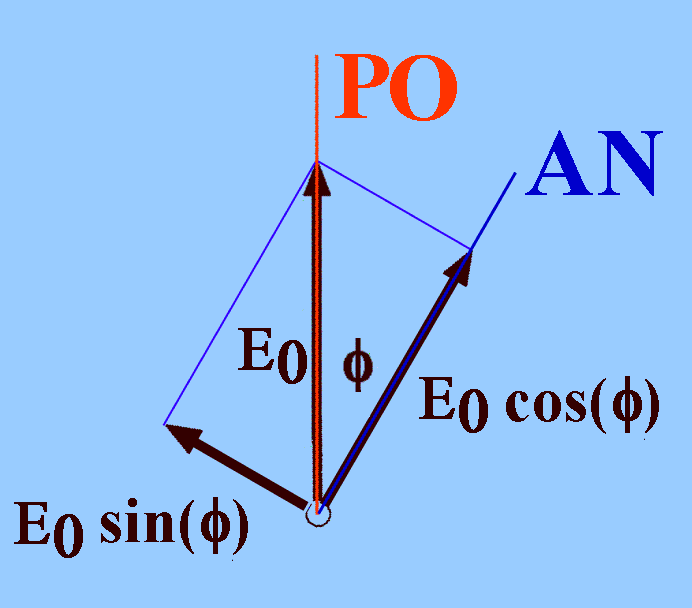Gemäß der klassischen Überlegung zum Durchgang von Licht erst durch einen Polarisator PO und dann durch einen dazu verdrehten Analysator AN wollen wir eine Komponentenzerlegung des Polarisationsvektors durchführen: Wenn der Vektor des elektrischen Felds E nach dem Durchtritt durch den Polarisator (PO) den Betrag E0 erhalten hat, lässt er sich bzgl. der Analysator-Richtung (AN) in eine parallele Komponente E0.cos(φ) und eine senkrechte Komponente E0.sin(φ) aufspalten. Wenn nicht gerade φ = 900 gibt es also immer eine Komponente parallel zum Analysator. Wenn wir jetzt unser "Übersetzungsschema" gemäß I.2.3 anwenden, entspricht das Amplitudenquadrat E02·cos2(φ) der Wahrscheinlichkeit P = cos2(φ) des Durchtritts eines Photons durch den Analysator, wenn der Analysator AN gegenüber dem Polarisator PO um den Winkel φ gedreht ist. Bei einer klassischen elektromagnetischen Welle wäre die Amplitude um den Faktor cos(φ) geschwächt, und damit auch die Intensität des Lichts, die proportional zu E02·cos2(φ) wäre, um den Faktor cos2(φ). Sie würde mit dem Winkel φ gleichmäßig abnehmen. Dem gegenüber gehorcht der tatsächliche Durchtritt von einzelnen Photonen dem objektiven Zufall; auch, wenn eine von Null verschiedene Durchtrittswahrscheinlichkeit besteht, kann es sein, dass ein einzelnes Photon gesperrt wird, während sein genau gleicher Nachfolger durchgelassen wird. (Tatsächlich sind die Verhältnisse auch bei einer quantentheoretischen Betrachtung der elektrischen Feldstärke noch etwas komplizierter, weil bei Fock-Zuständen, wie wir sie für einzelne Photonen brauchen, die Entsprechung der elektrischen Feldstärke ("Diagonalelement" von E) immer 0 ist. Die richtige quantentheoretische Behandlung - sie verwendet dann auch das Vektorpotential A statt E und B - führt aber dennoch zum gleichen Ergebnis. Damit wollen wir uns hier aber nicht beschäftigen.) (7) An einem einzelnen Photon ist so gar nicht feststellbar, welche Polarisation es vor der Messung hatte. Das hatten wir schon früher verschärft zu der Behauptung, dass ein Quantensystem eine Eigenschaft vor ihrer Messung i.A. nicht besitzt. Vor der Messung ist die Polarisation objektiv un-be-stimmt. (Siehe Grundfaktum Id: objektive Un-be-stimmtheit ). Nach dem Durchgang durch den Polarisator hat es sicher die Polarisationseigenschaft, die die Polarisationsrichtung des Polarisators anzeigt.
I.5.7 Hinweis auf analoge Versuche mit Elektronen (Spin)	Die Polarisation eines Photons hängt eng mit seinem Drehimpuls zusammen, der bei Photonen ganzzahlig ist. Freie Elektronen haben ebenfalls einen Drehimpuls, der halbzahlig ist und Spin heißt. Auch hier liefert die  Messung einer Messgröße (Elektronenspin bzgl. einer bestimmten Orientierung, z.B. parallel zur z-Achse) ein be-stimmtes Ergebnis. Bzgl. einer dazu komplementären Messgröße (z.B. Elektronenspin bzgl. einer dazu senkrechten Orientierung, etwa parallel zur y-Achse) sind die Messwerte dann völlig un-be-stimmt. Bei deren Messung ergeben sich dann zufällige Werte: Die Spin-Komponenten bzgl. zueinander senkrechter Richtungen sind komplementär.
I.5.8 diskrete Werte	(8) Vorgreifend wird darauf hingewiesen, dass merkwürdigerweise in vielen Fällen eine Messgröße in einer Messung nur ganz be-stimmte diskrete Messwerte erhalten kann, z.B. die Energie eines H-Atoms oder eines Elektrons in einem Potentialkasten. Diskrete Messwerte sind einzelne Messwerte, die durch "verbotene" Bereiche voneinander getrennt sind. (Grundfaktum IVe: Existenz von diskreten Meswerten) Das ist ein von der klassischen Physik her unerwarteter Effekt, der dem ganzen Fachgebiet den Namen einbrachte: "Quantenphysik", wegen der diskreten Energie-Quanten (Energieportionen, Energiepakete von Quantum = Portion), die z.B. Photonen bei Licht einer bestimmten Farbe haben müssen. Es gibt allerdings ein klassisches Analogon: Schwingende Saiten, schwingende Luftsäulen, wie Orgelpfeifen, oder schwingende Platten und Membranen, wie ein Paukenfell, haben eine oder mehrere Eigenschwingungen mit bestimmten diskreten Eigenfrequenzen. (Würde man solche diskreten Eigenfrequenzen mit dem Planckschen Wirkungsquantum h multiplizieren, so würde man formal zu diskreten Energien kommen.)