 |
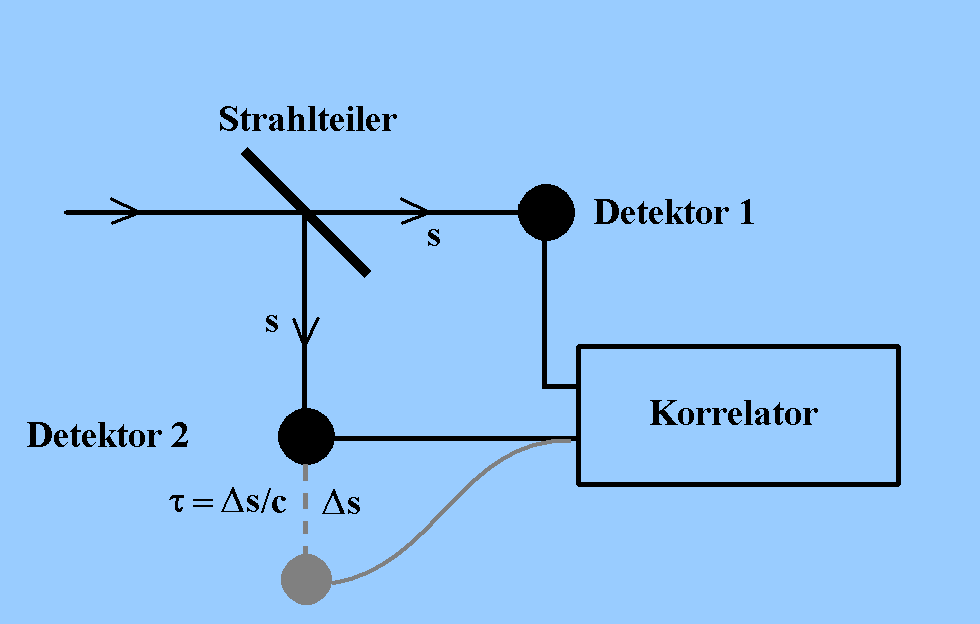
(1) Strahlung einer thermischen Lichtquelle trifft auf
einen Strahlteiler. Jeweils die halbe Strahlungsleistung trifft
auf Detektor 1 bzw. Detektor 2. Die Ausgangssignale beider
Detektoren werden in einem Korrelator miteinander
verglichen.
Ein Korrelator multipliziert beide Signale miteinander
und mittelt sie über ein bestimmtes Zeitintervall T. Bei
thermischem Licht - es mag chaotisch sein wie es will - und bei
gleichen Abständen s der Detektoren vom Strahlteiler sollten die
beiden Signale weitgehend übereinstimmen. Wenn die Photonen
vollkommen zufällig auf den Strahlteiler eintreffen, sollte es
zu zufälligen Koinzidenzen (gleichzeitiges Ansprechen) kommen.
Wenn die Photonen aber "korreliert" sind, sollte es darüber
hinaus zu weiteren Koinzidenzen kommen.
|
| (2) Es handelt sich um "Intensitätskorrelationen", weil
beide Signale proportional zur momentanen Intensität I bzw. zur
Anzahl n der einfallenden Photonen sind.
(3) Detektor 2 kann zusätzlich noch um die Strecke Δs
verschoben werden. Das Licht auf diesem Weg trifft dann -
klassisch argumentierend - um eine Zeit τ = Δs/c verzögert
am Detektor ein.
|
(4) Das Ausgangssignal des Korrelators kann dann
beschrieben werden als proportional zu k =
<I(t)·I(t+τ)>/<I(t)>2. I(t) ist dabei die
momentane Intensität, die spitzen Klammern deuten die zeitliche
Mittelung über ein bestimmtes Zeitintervall T an. Indem durch das
Quadrat der mittleren Intensität dividiert wird, wird "auf 1
normiert": Bei rein zufälligen Koinzidenzen, ohne "Korrelation",
sollte der Ausdruck k = 1 ergeben. |
(5) Der Ausdruck für k bleibt im Wesentlichen
unverändert, wenn man die Intensitäten I durch die zugehörigen
Teilchenzahlen n ersetzt. k ist dann proportional zu
<n(t)·n(t+τ)>/<n(t)>2.
|
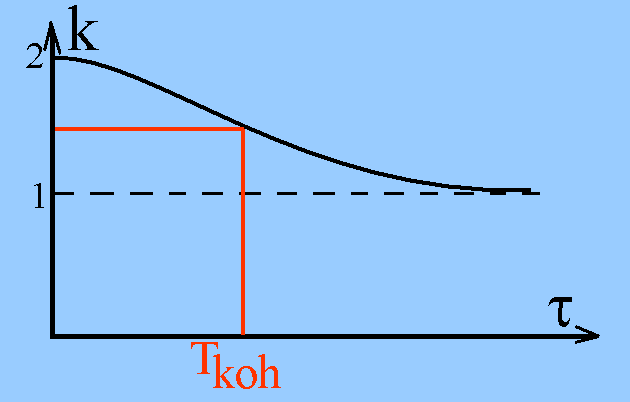
(6) Bei chaotischem und thermischem Licht ergibt sich für
k dem gegenüber eine Kurve gemäß der nebenstehenden Zeichnung. Was
kann man aus ihr herauslesen? Offenbar treten bei kleinen
Verzögerungszeiten τ vermehrt Koinzidenzen ein: Auf ein
nachgewiesenes Photon folgt bei thermischem Licht kurz darauf
mit Vorliebe ein weiteres. Diesen Effekt nennt man "Bunching"
(Häufung). Das ist ein typischer Quanteneffekt, der nichts mit der
Bose-Einstein-Statistik der Photonen zu tun hat, vielmehr Ausdruck
der starken Intensitätsschwankungen von chaotischem Licht ist. Für
sehr große Verzögerungszeiten τ geraten die beiden Photonengruppen
immer mehr "außer Takt" und nähern sich dem Verhalten
unkorrelierter Photonen. Die Korrelation k sollte also für sehr
große τ gegen 1 streben, wie es die Messung auch zeigt. |
| (7) Als Maß für den Bereich, in dem die eintreffenden
Photonen stark korreliert sind, nimmt man die Kohärenzzeit Tkoh,
die sich z.B. wie in der Zeichnung für thermisches Licht bestimmen
lässt. |
(8) Bei kohärentem Laserlicht ergibt sich eine
ganz andere Kurve. Dort ist k immer 1, unabhängig von der
Verzögerung τ! Grund dafür ist die Poisson-Verteilung der
Photonenzahlen bei kohärentem Licht: Hier ist die Photonenzahl
un-be-stimmt. Misst man diese immer wieder, so erhält man die
unterschiedlichsten Poisson-verteilten Ergebnisse.
|
Thermisches Licht zeigt
"Bunching", Laserlicht nicht!
|
Man kann auch "nicht
klassisches Licht" erzeugen, bei dem auf ein
nachgewiesenes Photon erst nach einiger Zeit ein weiteres Photon
folgt. Diesen Effekt für nicht klassisches Licht heißt man "Antibunching".
|

