(1) Nach der Quantentheorie des Lichts sind Teilchenzahl (Photonenzahl) und Phase einer elektromagnetischen Welle nicht gleichzeitig messbar. Für beide Messgrößen besteht also eine Un-be-stimmtheits-Relation (HUR). Insbesondere bei chaotischem Licht, das etwa von einer thermischen Lichtquelle ausgeht, sind Intensitäts- und Phasenfluktuationen leicht einsichtig wegen der endlichen Emissionsdauer der Atome, und weil sehr viele Atome beteiligt sind, die unabhängig voneinander strahlen. Auch die Polarisationsrichtung der ausgesandten Photonen fluktuiert.

(2) Führt man einen Hanbury-Brown/Twiss-Versuch (HBT) mit solchem (thermischem) Licht durch*), beobachtet man ein völlig zufälliges Ansprechen der Detektoren, aber auch eine starke Korrelation zwischen den Ereignissen der beiden Detektoren: Wenn ein Detektor ein Photon nachweist, wird mit erhöhter Wahrscheinlichkeit gleich darauf auch durch den zweiten Detektor ein Photon nachgewiesen: Die starken Fluktuationen wirken sich offenbar so aus, dass Photonen gern "gebündelt" auftreten. Man spricht von Photonen-"Bunching". Zugrunde liegt die Bose-Einstein-Statistik für Photonen. Sie bewirkt, dass Photonen vor allem die niedrigsten Energiezustände einnehmen, mit Vorliebe sogar die gleichen.

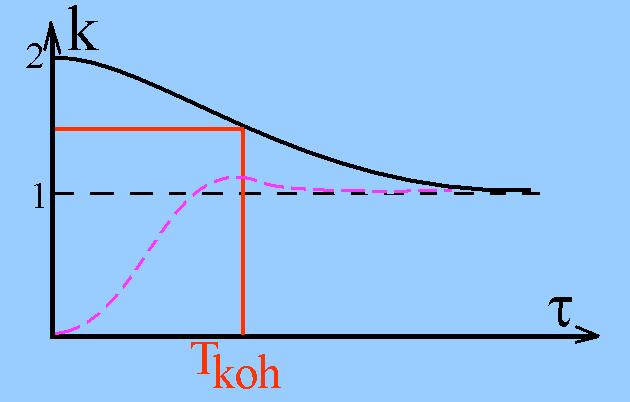
Korrelationsfunktion k in Abhängigkeit von der Verzögerungszeit t bei thermischem Licht (schwarz). Das Maximum bei t = 0 zeigt eine erhöhte Wahrscheinlichkeit für das Auftreten zweier Photonen mit sehr geringem Zeitabstand t an.

(3) Führt man aber einen HBT-Versuch mit Laserlicht durch, erhält man ein völlig anderes Verhalten: Die einzelnen Photonennachweise erfolgen auch hier zufällig, aber völlig unkorreliert. Es ist vollkommen gleichgültig für die Nachweiswahrscheinlichkeit, ob gerade ein Photon nachgewiesen wurde: "Laser-Photonen haben keine Geschichte". Jeder Zeitabstand zwischen zwei Photonen ist gleich wahrscheinlich. Das hängt damit zusammen, dass Laserlicht sehr gut durch kohärente Zustände beschrieben wird. Das sind Zustände, bei denen die Photonenzahl (in einer bestimmten Zeit oder in einem Laserpuls) einer Poisson-Verteilung genügt (und also un-be-stimmt ist). Bei einer großen mittleren Photonenzahl sind Photonenzahl und Intensität recht scharf um einen bestimmten Mittelwert konzentriert: Die relativen Intensitätsfluktuationen sind recht gering. In der Abbildung entspricht die für Laser-Photonen zuständige Korrelationsfunktion der gestrichelten horizontalen Linie.

(4) Bei klassischem Licht ist für die Korrelationsfunktion nur der Bereich >= 1 erlaubt. Die violette Kurve ragt aber in den Bereich <1 hinein. Die Wahrscheinlichkeit für den Nachweis eines weiteren Photons ist dort also geringer als bei reinem Zufall. Für kleine Zeiten t folgt dann auf ein nachgewiesenes Photon zunächst kein weiteres. Solches Licht nennt man nichtklassisches Licht. Es kann künstlich hergestellt werden durch nichtlineare optische Prozesse. Aber auch schon ein einzelnes Ion in einer Falle strahlt bei Resonanzfluoreszenz mit eingestrahltem Laserlicht nichtklassisches Licht aus.

Die Photonenfolgen für die drei Arten von Licht zeigt schematisch die nachfolgende Abbildung:

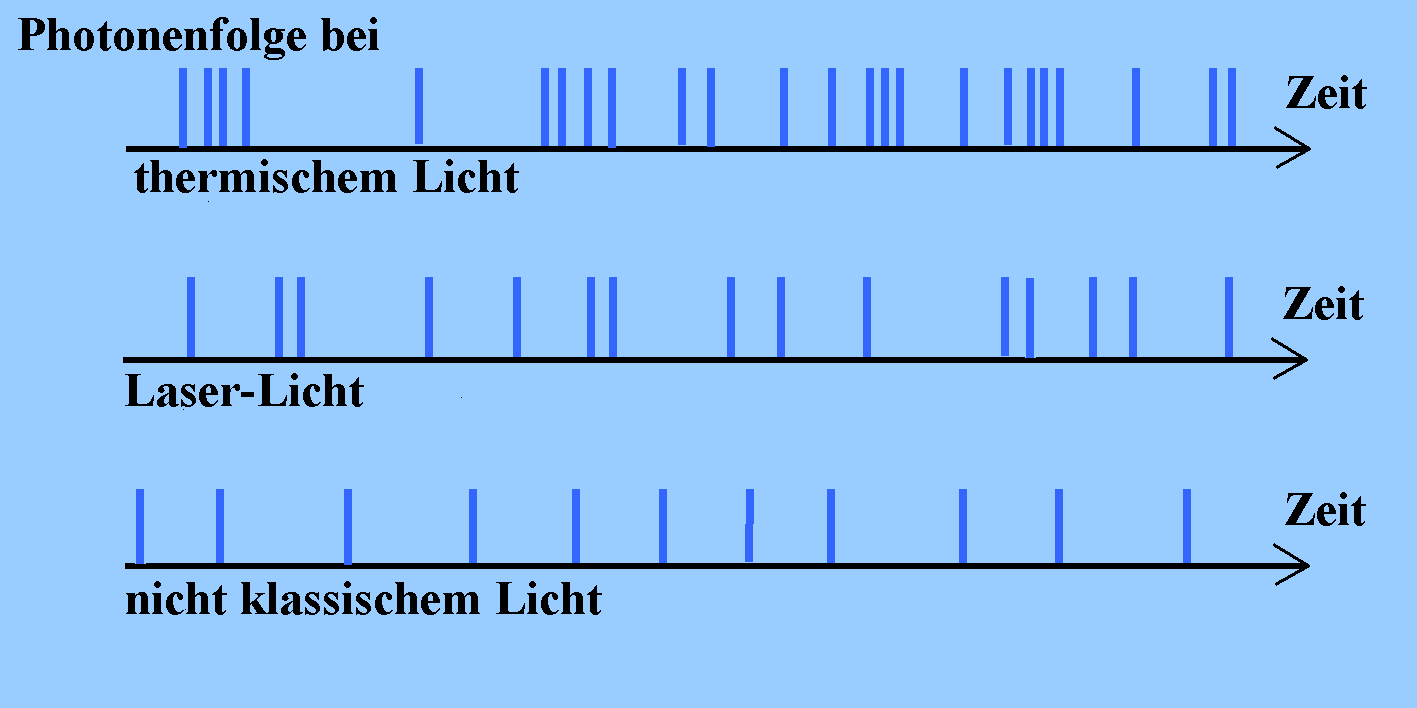Man erkennt das Bunching bei thermischem Licht also Folge der starken Intensitätsfluktuationen. Bei klassischem Laserlicht sind die Intensitätsfluktuationen relativ gering. Die Zeitabstände zwischen zwei aufeinanderfolgenden Photonen sind ähnlich verteilt wie beim radioaktiven γ-Zerfall. Bei nichtklassischem Licht tritt tendenziell nach jedem Photonen-Nachweis erst einmal eine Pause ein (antibunching). Das hängt auch hier mit sehr geringen Intensitätsfluktuationen zusammen. Bei einem einzelnen Ion in einer Falle ist das anschaulich verständlich: Nach einem Emissionsvorgang muss das Ion erst wieder Energie aus dem anregenden Laser aufnehmen . Die ausgesandten Photonen halten sich so zeitlich auf Abstand.

^*) Eigentlich möchte man mit einem einzigen Detektor die Photonenfolge vermessen. Weil aber jeder Detektor nach einer Messung erst einige Zeit "tot", also unempfindlich ist, wendet man den Trick mit der HBT-Anordnung an. Es besteht dann eine gewisse Chance, dass nach dem Photon, das mit Detektor 1 nachgewiesen wurde, ein Photon folgt, das am Strahlteiler den zweiten Weg wählt.

=> Klassisches und nicht klassisches Licht (2)