Das Michelson-Stellar-Interferometer ist ein Gerät zur Bestimmung von großen Sterndurchmessern und zur Unterscheidung zwischen Sternen und Doppelsternen.

Basis ist ein abgewandelter Doppelspalt-Versuch mit Licht aus dem optischen Bereich. Die Prinzip-Funktion soll jetzt schrittweise erläutert werden, wobei das Ziel ist zu verstehen, wie prinzipiell der (Winkel-)Abstand zweier punktförmiger und monochromatischer Lichtquellen bestimmt werden kann.

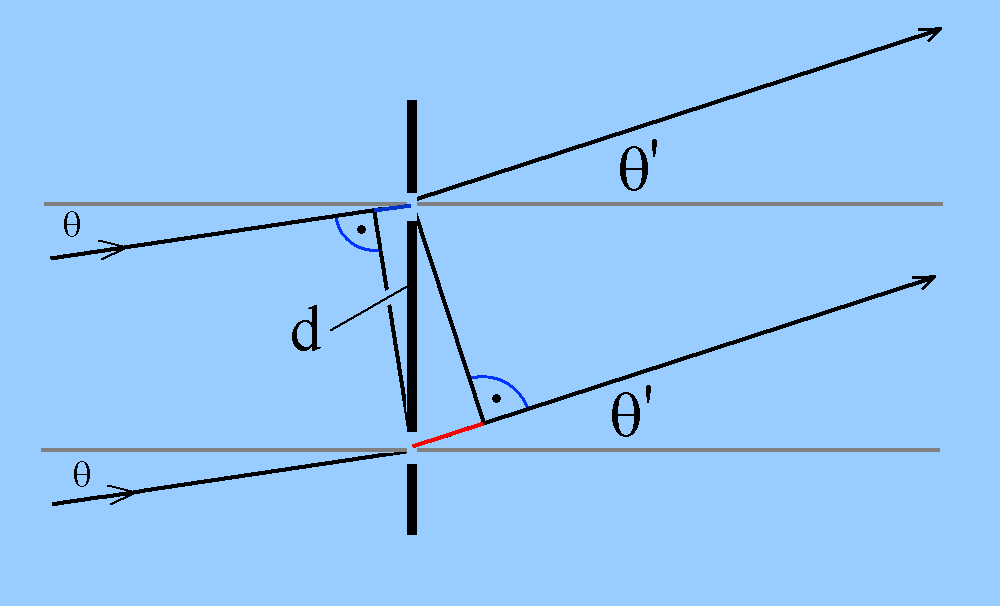
(1) Von einer punktförmigen Lichtquelle soll monochromatisches Licht der Wellenlänge λ unter einem Winkel θ gegenüber der Symmetrieachse auf einen Doppelspalt mit Spaltabstand d einfallen. Die Spaltöffnungen verlassen jetzt Kreiswellen mit vielen Wellennormalen, u.a. die eingezeichneten parallelen Strahlen mit einem Winkel θ' gegenüber der Symmetrieachse. Sie überlagern sich im Unendlichen. Zwischen den zwei gezeichneten Strahlen entstehen zwei Gangunterschiede Δs1 = d·sin(θ) und Δs2 = d·sin(θ'), zusammen also der Gangunterschied ΔS = d·[sin(θ) - sin(θ')], oder in Kleinwinkel-Näherung: ΔS = d·[θ - θ'] .	(2) Nehmen Sie an, dass jetzt zwei punktförmige Lichtquellen mit den Einfallswinkeln θ1 und θ2  ihr Licht gegen den Doppelspalt senden. Für die Lichtquelle 1 soll unter dem Winkel θ' gerade das 1. Maximum liegen. Dann gilt:             ΔS(1) = d·[ θ1 - θ'] = k·λ  (k = 1) Unter dem gleichen Winkel θ' soll aber von der Lichtquelle 2 gerade das 0. Minimum (neben dem zentralen Hauptmaximum) liegen, also             ΔS(2) = d·[θ2 - θ'] = λ/2 . Dann heben sich unter diesem Austrittswinkel θ' Maximum und Minimum gerade auf. Ähnliches passiert bei allen anderen Stellen früherer Maxima bzw. Minima. In dieser Situation gibt es keine Interferenz, obwohl jede Lichtquelle für sich ein Interferenzbild geben würde.
(3) Aus den Gangunterschieden errechnen Sie:  d·( θ1 - θ' ) = 2·d·(θ2 - θ' ) = λ  oder   θ1 - θ2 = λ/(2·d). Das ist gerade der Winkelabstand Δθ der beiden punktförmigen Lichtquellen. Er erfordert für eine bestimmte Wellenlänge λ einen bestimmten Spaltabstand d, damit die Interferenz verschwindet. Im Prinzip könnte man zur Bestimmung des Winkelabstands Δθ der beiden punktförmigen Lichtquellen also so vorgehen: Von sehr kleinen Werten d ausgehend wird d so weit vergrößert, bis das erste Mal die Interferenz verschwindet. Diesen Abstand d nennt man auch die transversale Kohärenzlänge des Lichts. Nach der Formel Δθ  = λ/(2·d) erhält man  dann den Winkelabstand aus dem so gemessenen d und der Wellenlänge λ.	(4) Leider ergibt sich bei typischen Werten von d = 0,1 m und λ = 500 nm eine Winkeldifferenz von ca. 0,5" . Weil so große Sterne (außer der Sonne) nicht bekannt sind, ist die Methode so also noch ungeeignet um Sterndurchmesser zu bestimmen. Eine höhere Winkel-Auflösung würde sehr viel größeres d (einige Meter) erfordern mit dem Nachteil, dass dann der Streifenabstand zu gering wäre. Die Interferenz kann ins Endliche geholt werden, wenn die Parallelstrahlen durch eine Linse in ihre Brennebene fokussiert werden.
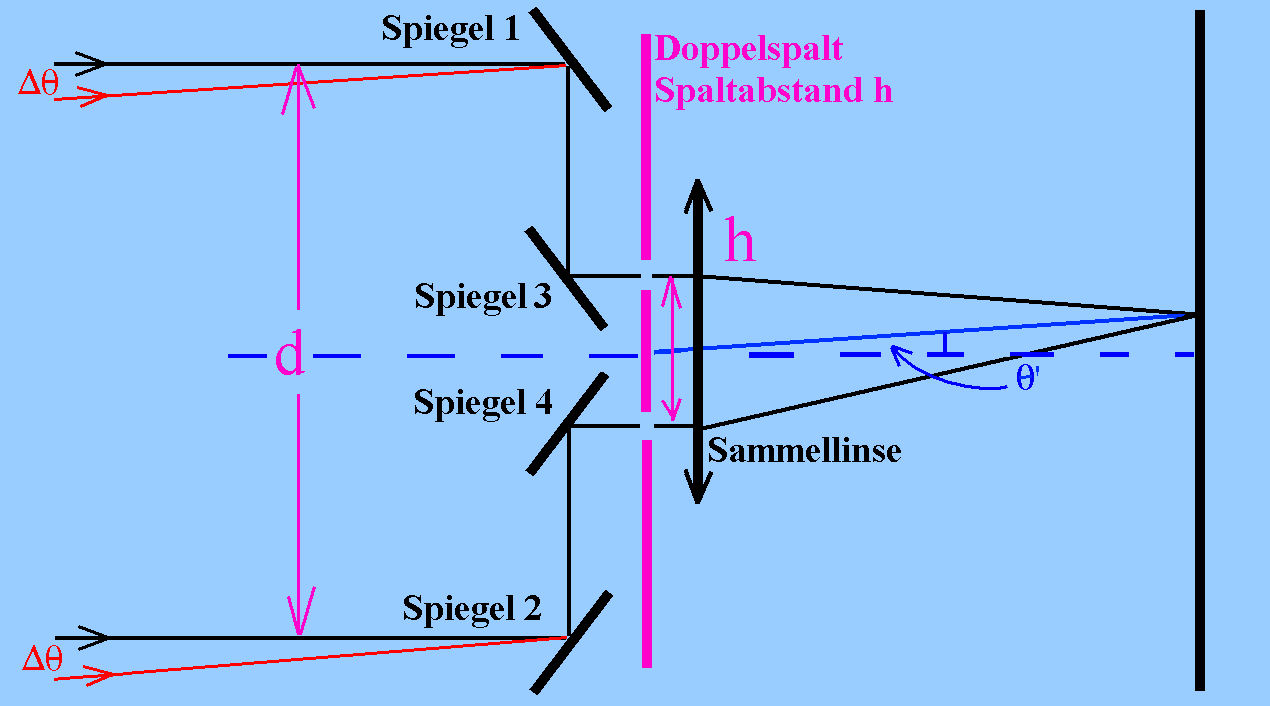
	(5) Michelson hatte die Idee, die Auflösung durch ein großes d zu steigern und trotzdem noch den Streifenabstand relativ groß zu halten. Das gelingt mit einen kleinen Spaltabstand - er soll jetzt h heißen. Dazu setzte er Umlenk-Spiegel vor die Linse mit ihrem Doppelspalt, durch die die Öffnung des Interferometers deutlich gesteigert wurde. Der unveränderte Spaltabstand h bestimmt den Linienabstand in der Beobachtungsebene, die Auflösung wird durch d bestimmt.
(6) Bei der Messung des Winkelabstands zweier Doppelsterne beginnt man also mit kleinem d. Dabei sollte man ein klares Interferenzmuster beobachten. Dann erhöht man d bis das Interferenzmuster das erste Mal verschwunden ist und misst den dazu gehörigen Abstand d der Eintrittsstrahlen (die transversale Kohärenzlänge des Lichts). Wie oben erhält man den Winkelabstand Δθ, leider immer noch nur für große Sterne (bis herunter zu 0,02"), weil d aus Stabilitätsgründen beschränkt ist. Atmosphärische Störungen und das Wellenlängenspektrum "verschmieren" die Interferenz ebenfalls, so dass der Nutzen des Geräts beschränkt ist. Auch mit dem Hanbury-Brown/Twiss- Stellar-Interferometer wird primär die transversale Kohärenzlänge ermittelt, allerdings mit "Intensitätskorrelationen" statt mit Interferenz.	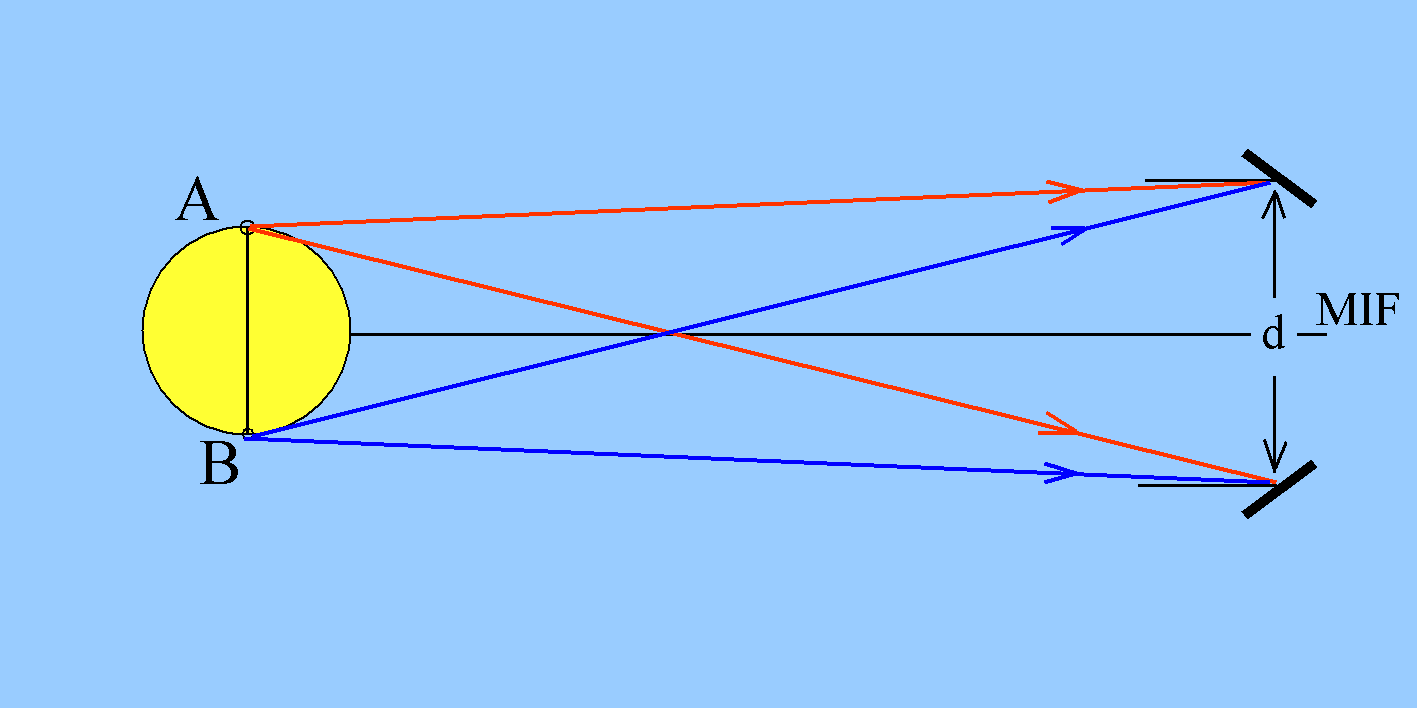(7) Wie ist es überhaupt möglich, dass Licht von einem ausgedehnten Stern interferiert? Das Bild zeigt es: Die gleichfarbigen Strahlen interferieren im rechts weggelassenen Fernrohr, wenn ihr Gangunterschied geringer als die Kohärenzlänge (und in der Größenordnung von wenigen Wellenlängen) ist. Wenn die Kohärenzbedingungen erfüllt sind, könnten z.B. beide Strahlenpaare zu einem Maximum beitragen. Zur Messung des Winkeldurchmessers muss man durch Veränderung von d die Situation einstellen, wo das eine Strahlenpaar zu einem Maximum beiträgt, das andere zu einem Minimum an gleicher Position.

E

1. Mit Hilfe von Doppelspalt-Interferenz lässt sich der Winkeldurchmesser großer Sterne (Roter Riesen) und der Winkelabstand von Doppelsternen messen. 2. Genutzt wird dabei die übliche Interferenz, die im klassischen Fall als Interferenz von elektrischen Feldstärken (bzw. ihrer Amplituden) gedeutet werden kann.