Fließt ein Wechselstrom auf oder durch den
Kondensator? |
Häufig wird für einen Wechselstrom oder auch den Ladestrom (Gleichstrom) in einem Stromkreis mit einem Kondensator Folgendes behauptet: Es handle sich um einen unterbrochenen Stromkreis. Ein Strom komme deshalb nur dadurch zustande, dass in einer bestimmten Zeitphase Ladungen auf die eine Kondensatorplatte fließen, während gleichzeitig von der anderen Platte Ladungen wegfließen. Durch den Kondensator können keine Ladungen fließen. Der Vorgang ist offenbar richtig beschrieben. Eine falsche Behauptung entsteht aber, wenn behauptet wird, dass durch den Kondensator kein elektrischer Strom fließe.
.
Denn: Neben dem mit dem Transport von Ladungen verbundenem Leitungsstrom gibt es andere elektrische Ströme, die nicht unbedingt mit dem Transport von Ladungen verbunden sind, z.B. ein Magnetisierungsstrom oder Polarisationsstrom in Materie, oder ein Verschiebungsstrom im Vakuum ganz ohne Ladungstransport, wenn sich das elektrische Feld dort zeitlich ändert.
Es gilt die Maxwell-Gleichung:
(3) rot B = µ0 j mit der Stromdichte
j, wobei
Dabei ist die Dichte des Verschiebungsstroms gegeben durch:
Zur Kontrolle [ε0 ] = As/V·m, [dE/dt] = V/m·s, also [jV] = A/m2 , wie es bei einer Stromdichte sein muss.
(Hinweis: Es gilt µ0
· ε0 = 1/c2 mit
der Lichtgeschwindigkeit c. Eine andere Form der Maxwell-Gleichung (3) ist
also: rot B = - 1/c2 · dE/dt , die zusammen
mit dem Induktionsgesetz für die Ausbreitung elektromagnetischer Wellen
zuständig ist.).
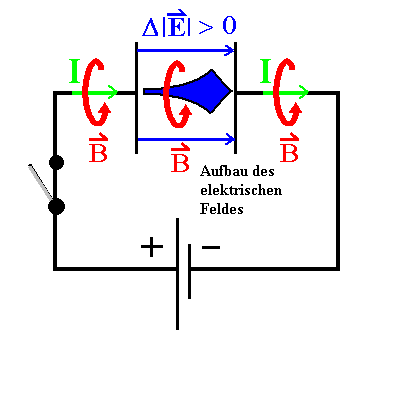 |
Abb. 1: Der sich weitende Pfeil für die elektrische Feldstärke deutet an, dass sich das (homogene) elektrische Feld der eingezeichneten Richtung im Laufe der Zeit verstärkt. Betrachten wir einen Kondensator mit Vakuum zwischen den Platten.
Es gilt Q = C·U bzw. dQ/dt = Iext = C·dU/dt
= ε0 ·A/d· dU/dt
= ε0·A·dE/dt
= jV·A = I (jeweils mit Beträgen).
Iext soll dabei der Strom "auf" den Kondensator oder "vom" Kondensator sein, der Lade- bzw. Entladestrom oder Leitungsstrom.
Durch die kleine Rechnung hat es sich also herausgestellt, dass dieser Strom von gleicher Größe wie der Verschiebungsstrom IV durch den Kondensator ist.
|
Beim Laden und Entladen eines Kondensators fließt außerhalb
des Kondensators ("auf" den Kondensator und "vom" Kondensator) ein Leitungsstrom
Iext und zwischen den Kondensatorplatten ("durch" den Kondensator)
ein Verschiebungsstrom IV gleicher Größe, der nicht
mit dem Transport von Ladungen verbunden ist. |
Beide Ströme erzeugen ein Magnetfeld entsprechend dem Ampere'schen
Gesetz bzw. Biot-Savart-Gesetz. Das Magnetfeld werde gemessen auf einem
konzentrischen Kreisring mit dem Radius r um den Leiter. Wenn der Strom
vollständig erfasst wird, entsteht bei gleichem Radius r in beiden
Fällen ein gleich starkes Magnetfeld. Innerhalb des Kondensators hat
man die Möglichkeit, den Kreisring kleiner zu wählen, so dass nur
ein Teil des Stroms erfasst wird. Dann erhält man auch ein kleineres
Magnetfeld. So könnte man im Prinzip die Magnetfelder experimentell
unterscheiden, die durch den Leitungsstrom und den Verschiebungsstrom erzeugt
werden.
Dass der Strom auf den Kondensator auch durch den Kondensator weiterfließen
muss, ist eine Folge der Kontinuitätsgleichung.
