|
SG111 Wie sollten wir die Kapazität des Plattenkondensators definieren? ©
H. Hübel Würzburg 2013
|
Impres-sum |
Mehr hierzu in:
 |
Abb. 1: Im Schülerversuch soll ein Probe-Kondensator C' (z.B. 1 µF) bei einer bestimmten Ladespannung U geladen werden. Über einen Ladungsmesser wird der Probe-Kondensator wieder entladen und die gespeicherte Ladungsmenge Q gemessen. Fragestellung: Wie hängt die Ladung Q auf dem Probe-Kondensator von der Ladespannung U ab? Das Versuchsergebnis legt die Definition einer Kapazität C = Q/U nahe. |
 |
Ein Ladungsmesser für
Schülerversuche (Abb. 2)
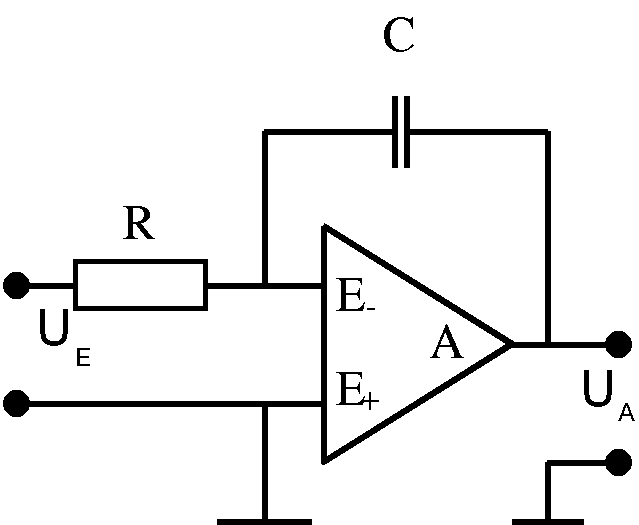
Grob vereinfacht funktioniert er folgendermaßen nach zwei allgemeinen Prinzipien bei Operationsverstärkern: 1. Durch den beschalteten OV wird die Spannung zwischen den Eingängen E- und E+ so geregelt, dass sie nur um wenige mV voneinander abweicht. Vereinfacht geht man davon aus, dass sie Null, dass beide Eingänge auf "virtueller Masse" liegen. 2. Der Eingangswiderstand ist beliebig hoch: es kann kein Strom in die Eingänge hinein fließen. 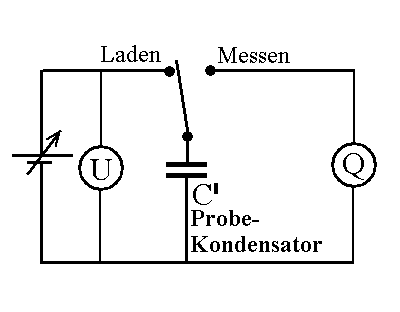Was geschieht nun, wenn eine Spannung zwischen E1 und Masse angelegt wird, weil z.B. beide Pole an einem geladenen Kondensator liegen. Die Ladung muss über R zur Masse abfließen. Es fließt ein Strom durch R, der nur von U und R abhängt: I = U/R Aber dieser Strom kann wegen des beliebig hohen Eingangswiderstands nicht in den OV hineinfließen. Er muss über den Rückkopplungszweig auf den Mess-Kondensator C fließen, der sich dadurch auflädt. Der Vorgang ist beendet, wenn alle Ladungen vom externen Kondensator abgeflossen sind. Zwischen Ausgang und (virtueller) Masse liegt dann die Ladespannung von C. Diese ist ein Maß für die Ladung auf dem externen Kondensator. 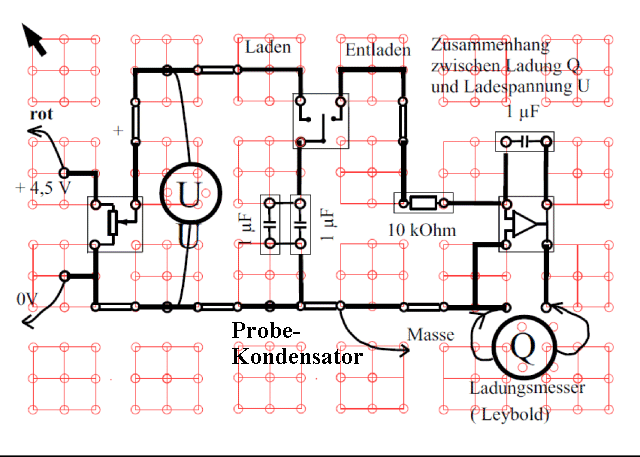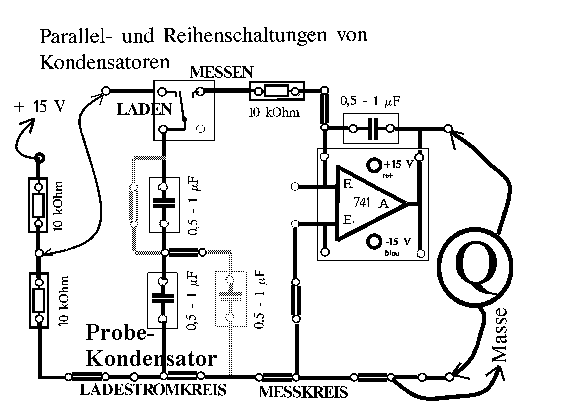Ein solcher Ladungsmesser ist in der Regel unempfindlicher als ein handelsüblicher von einer Lehrmittelfirma. Er ist für einen Schülerversuch dagegen leicht und kostengünstig aufzubauen, und für viele Situationen reicht seine Empfindlichkeit aus. C sollte für diesen Versuch in der Größenordnung von C' sein, aber C =/= C'. Wenn C = 1 µF lassen sich Ladungsmengen in der Größenordnung von 1 µAs nachweisen. Vgl. auch: Test des Ladungsmessers |
 |
Abb. 3: Im Schülerversuch lässt sich der
Zusammenhang zwischen Ladung Q und Ladespannung U leicht
untersuchen (Auflageblatt für die Leybold-Rastersteckplatte)..
In der Schaltung links wird als Ladungsmesser eine bestimmte Operationsverstärker-Schaltung ("Integrator") verwendet. Diese Schaltung pumpt alle Ladungen, die ihm angeboten werden, auf einen Mess-Kondensator und misst anschließend verlustlos die Ladespannung als Maß für die geflossene Ladung. Mit dem Potentiometer wird bei Schalterstellung "Laden" die Ladespannung U eingestellt. In der Schalterstellung "Entladen" wird die Ladung Q auf dem Probekondensator gemessen und durch ein Messgerät angezeigt. Die positive und die negative Betriebsspannung ist hier nicht eingezeichnet. |
Ergebnis:
Der Versuch zeigt eine Proportionalität zwischen Ladespannung U und Ladung Q.
| Die konstante Steigung
des U-Q-Graphen (Q nach oben, U nach rechts) wird als
Kapazität C definiert:
C = Q/U |
mit der Einheit
[C] = 1 A·s/V = 1 F (Farad) nach Michael Faraday.
 |
Abb. 4: In einer Versuchsvariante wird ganz
entsprechend die Kapazität von Parallel- und Reihenschaltung
von Kondensatoren untersucht (Auflageblatt für die
Leybold-Rastersteckplatte).
Der Versuch könnte so auch die Definition von C = Q/U vertiefen, obwohl hier eine theoretisch Herleitung naheliegend ist. |
 |
Abb. 5: Schülerversuchs-Anordnung - die
Ladespannung U wird mit einem Spannungsteiler aus der
positiven Betriebsspannung abgeleitet (rotes Kabel).
Probekondensator C'.
Der OV wird hier über die Lehrsaal-Verkabelung mit der positiven und negativen Betriebsspannung und Masse versorgt. |
.
( Juni 2014 )