Mit einer Stromwaage wird die Kraft auf einen
stromdurchflossenen Leiter im Magnetfeld gemessen. Daraus ergibt sich
die Definition der magnetischen Flussdichte B.
In der Regel beschränkt man sich in der Schule auf
Situationen, bei denen die Richtung des Magnetfelds B und die
Stromrichtung (I) aufeinander senkrecht stehen. Die magnetische
Kraft F auf den stromdurchflossenen Leiter ist in jedem Fall
senkrecht zu B und zu I.
Sind B und I parallel, entsteht keine magnetische
Kraft.
| Wenn B nicht parallel zu I: F
senkrecht B, F senkrecht I.
Wenn B senkrecht I: F maximal.
Wenn B parallel zu I: F = 0 (keine
Kraft)
|
 |
Abb. 1: Nachweis: F prop. I bzw.
Windungszahl n bei konstanter magnetischer Flussdichte B
mit einer Digitalwaage (Auflösung 1 g Masse entsprechend einer
Kraft von 10 mN). Es wird eine Rahmenspule von 100 - 300 Windungen
verwendet.
Hier wie in der Anordnung von Abb. 2 ist die Spule bzw. der
Leiterbügel fest und es wird die Kraft auf den (beweglichen)
Magneten gemessen. Der Magnet sitzt auf der darunter stehenden
Digitalwaage auf.
Keine Kraft entsteht, wenn der Strom parallel zu
den Magnetfeldlinien fließt.
Die Kraftrichtung genügt der 3-Finger-Regel
der rechten Hand, die mit der technischen
Stromrichtung arbeitet.
(Es kann eine Digitalwaage zur Kraftmessung
verwendet werden, weil diese üblicherweise die Gewichtskraft
misst, aber für "übliche Orte" Gewicht in Masse umrechnet, die
dann angezeigt wird. Hier wird die Anzeige wieder zurück
gerechnet in die ursprünglich gemessene Kraft.)
|
 |
Abb. 2: Stromwaage: Nachweis F prop. I und
Bügellänge ℓ mit einfachem Stromleiter (auf Platine; 1 Windung)
und hochempfindlicher Digitalwaage (Auflösung 0,01 g Masse
entsprechend einer Kraft von 0,1 mN).
Der Schieberegler im Hintergrund dient zur
Feinjustierung der Stromstärke bzw. als Vorwiderstand zur
Strombegrenzung. Ein kleineres Bauteil (genügend belastbar)
würde nicht den Blick auf die wichtigeren Teile der Anordnung
verstellen.
|
Ergebnis:
Dies gilt insbesondere, wenn die Windungszahl n = 1
ist, wie in Abb. 2. Die Proportionalitätskonstante hängt offenbar vom
Magnetfeld ab. Deswegen ist es naheliegend, hierfür eine magnetische
Flussdichte B zu definieren:
mit der Einheit [B] = 1 N/A·m oder, da 1 N·m = 1 J = 1
V·A·s: [B] = 1 V·s/m2
Der Vektor B ist die eigentliche magnetische
Feldstärke. Der Name ergibt sich daraus, dass 1 V·s auch
magnetischer Fluss genannt wird, bezogen auf 1 m2 Fläche also
Flussdichte 1 V·s/m2. Aus historischen
Gründen ist mit dem Namen "magnetische Feldstärke" leider eine andere
Größe (H) belegt.
|
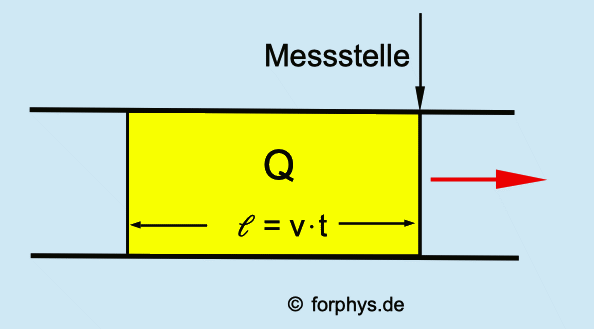
Abb. 3: Die magnetische Kraft auf den
stromdurchflossenen Leiter kommt durch die vielen Lorentz-Kräfte
auf die in ihm bewegten Ladungen zustande. Für eine einzelne
Ladung q gilt ja FL = q·v·B.
Bei einer Stromstärke I schiebt sich eine Ladungsmenge Q in der
Zeit t mit der Geschwindigkeit v durch einen Leiterquerschnitt,
also I = Q/t .
Q ist die Ladungsmenge, die in einem Zylinder der Länge
ℓ = v·t
enthalten ist: alle Ladungen in diesem Zylinder schieben
sich in der Zeit t an einer Messstelle vorbei.
Insgesamt ergibt sich F = Q·v·B
= Q/t·v·t·B
= I·ℓ·B
= B·I·ℓ
.
I · ℓ heißt manchmal "Stromelement". B = F/(I
· ℓ) ähnelt dann der Definition E = F/q für das elektrische
Feld, wenn die Ladung q durch das Stromelement I
· ℓ ersetzt ist.
|
.
( Juni 2014 )


