1. Eine äußere Kraft F greift an einem Ende der Feder an. Das
andere Ende der Feder ist frei. Die äußere Kraft F beschleunigt
die Feder als ganze (abgesehen von anfänglichen Trägheitseffekten).
2. Eine äußere Kraft F greift an einem Ende der Feder an. Das
andere Ende der Feder ist befestigt, wie etwa bei einer aufgehängten
Feder, an deren unterem Ende eine dehnende Kraft F angreift.
| |
|
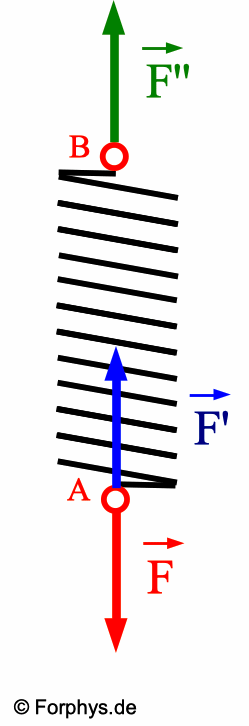
Die dehnende Kraft F ist die Ursache
einer Dehnung. Sie greift am Punkt A an. Sie allein könnte aber
die Feder nicht dehnen; sie würde die Feder als ganze nur in
ihre Richtung beschleunigen. Die Feder muss am Punkt B mit einer
Kraft F" festgehalten werden. F" wird "Haltekraft"
genannt. F und F" müssen entgegengesetzt
gleich sein, weil die Feder als ganze ruht
(Kräftegleichgewicht mit der als starren Körper aufgefassten
Feder zwischen der Haltekraft F'' und der dehnenden
Kraft F).
Woher kommt die Haltekraft F"? Am Punkt B herrscht Kräftegleichgewicht
zwischen F" und der an den Punkt B verschobenen
Kraft F. B wird nicht beschleunigt.
[ Nahe B kann man es auch anders
sehen: F als actio zieht nämlich auch an
der (nicht gezeichneten) Aufhängung (oberhalb von B) und
verformt sie. Es entsteht eine Reaktionskraft F"
gleichen Betrags. Sie greift am Punkt B an und hält ihn fest.
(Die actio F greift auch an der Aufhängung an und
verformt sie. Ihre Reaktionskraft gleichen Betrags greift am
Punkt B an und hält ihn fest.) ]
Beim Federpendel, bei dem eine Feder mit einem
Pendelkörper der Masse m belastet ist, ist es manchmal
sinnvoll, statt der dehnenden Kraft F eine
rücktreibende Kraft F' zu betrachten. Beide greifen
am gleichen Punkt A (bzw. der Masse) an. Statt von einer
Dehnung s spricht man hier von einer Auslenkung x. Man
stellt sich ein Koordinatensystem vor, dessen Ursprung in
die Ruhelage der Pendelmasse gelegt wird. x ist dann die
Koordinate des Orts längs der Feder. Wenn der Pendelkörper
durch eine dehnende Kraft F festgehalten wird, also
bei Kräftegleichgewicht, sind beide Kräfte
entgegengesetzt gleich: F = - F'.
Deshalb gilt für die rücktreibende Kraft ganz ähnlich:
und sogar vektoriell mit der Rückstellkraft
F' und dem Ortsvektor x:
Das Minuszeichen besagt: Rückstellkraft
F' und Ortsvektor x sind stets
entgegengesetzt gerichtet. Nur, wenn x
= 0, wenn sich also der Pendelkörper in der Ruhelage befindet,
verschwindet die Rückstellkraft. Sonst wirkt stets je nach der
Position x des Pendelkörpers wirkt eine Rückstellkraft
F' mit der Richtung und dem Betrag der
Gesetzmäßigkeit. Das gilt auch dann, wenn keine äußere Kraft F
vorhanden ist.
F' heißt Rückstellkraft, weil sie versucht, den
Pendelkörper stets in seine Ruhelage (x = 0)
zurückzustellen.
|
3. Keine äußere Kraft F: Bewegung unter dem
Einfluss der Rückstellkraft F'
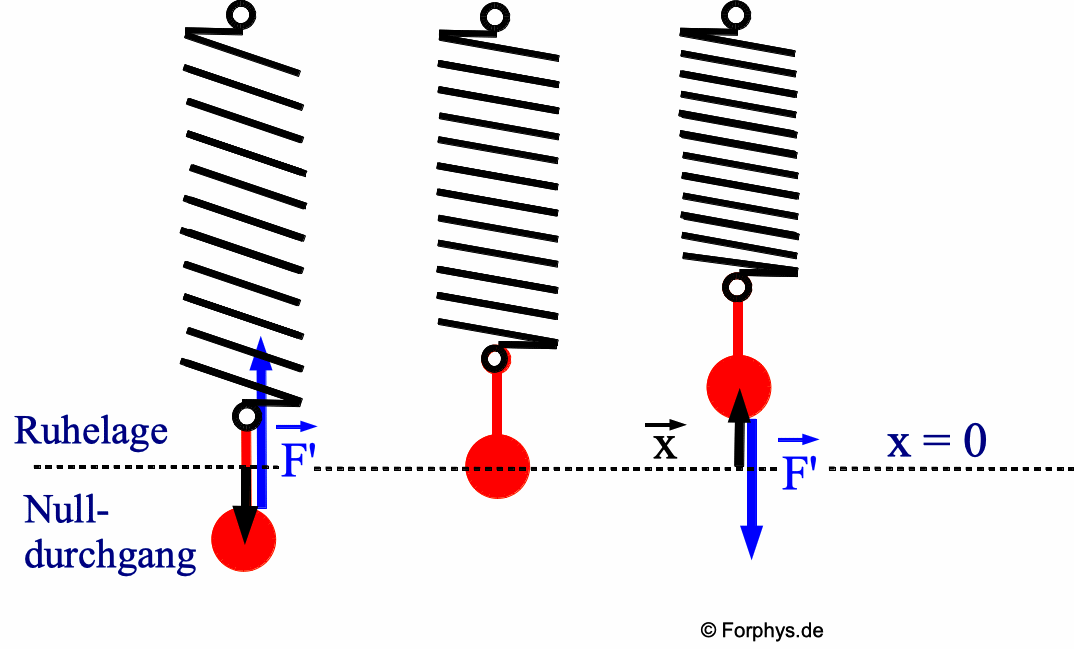 |
Die Rückstellkraft (rücktreibende
Kraft; blau) versucht stets, eine aus der Ruhelage ausgelenkte
Pendelmasse in die Ruhelage zurückzustellen. Ortsvektor x
(schwarz) und Vektor der Rückstellkraft (blau) sind stets
entgegengesetzt gerichtet. Wie ist die Rückstellkraft beim
Durchgang durch die Ruhelage ("Nulldurchgang")? |
Ohne die äußere Kraft F, also z.B. bei einer schwingenden
Pendelmasse im Fall des Federpendels, gilt immer noch actio
gegengleich reactio. Dabei greift F' als actio an der
schwingenden Masse (bzw. am Punkt A) an und beschleunigt diese.
Gleichzeitig wirkt die Reaktionskraft -F' auf den Punkt B (bzw.
die Aufhängung der Feder). Wenn zu einem bestimmten Zeitpunkt die
Kraft F' z.B. nach oben wirkt und die Pendelmasse nach oben
beschleunigt, greift an der Aufhängung die Reaktionskraft -F'
an, die die Aufhängung (Punkt B) nach unten zu ziehen versucht. Das
ist sehr ähnlich wie bei einer freien Feder, bei der zwei Körper an
ihren Enden entgegengesetzt zueinander beschleunigt werden (vgl. Bilder,
wobei die Feder hinzu gedacht wird).
Deshalb kann man beim Federpendel mit einem Sensor in der Aufhängung
auch die Kraft F' messen, mit der die Pendelmasse beschleunigt
wird.
Hinweis:
Zwei entgegengesetzt gerichtete Kräfte können am gleichen Punkt bzw.
Körper angreifen. Wenn sie gleichen Betrag haben, existiert Kräftegleichgewicht.
Die entgegengesetzt gerichteten Kräfte von "actio gegengleich
reactio" greifen an verschiedenen Körpern an. Sie haben
immer gleichen Betrag.
(vgl. SG072 Hooke'sches Gesetz).
*) Die Wirkung
einer Kraft hängt auch vom Angriffspunkt ab.
( April 2013)

