|
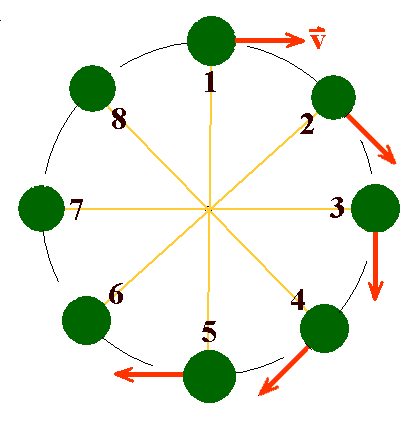
Eine gleichförmige Kreisbewegung liegt vor, wenn der Betrag v der Bahngeschwindigkeit v konstant ist. |
|
SG050 Kreisbewegung eines Massenpunktes ©
H. Hübel Würzburg 2013
|
Impres-sum |
Bei einer Kreisbewegung bewegt sich ein Massenpunkt auf einem Kreis. Die wichtigste Form der Kreisbewegung eines Massenpunktes ist eine so genannte gleichförmige Kreisbewegung.
 |
Der Vektor der Geschwindigkeit
("Bahngeschwindigkeit") v ändert sich ständig. Grund ist
eine ständige Beschleunigung a.
|
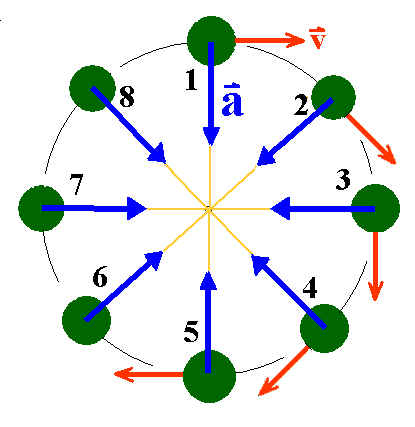 |
Bei einer gleichförmigen Kreisbewegung ist der
Beschleunigungsvektor a (blau) und damit auch die
wirkende Kraft F immer zum Zentrum der Bewegung hin
gerichtet (Zentralkraft, Zentralbeschleunigung). Mit a
hängen die ständigen Richtungsänderungen von v zusammen.
Hierbei wird der Geschwindigkeitsvektor v ständig geändert. Es findet also eine Beschleunigung statt. Trotz des Namens:
Bei einer gleichförmigen Kreisbewegung stehen a und v immer senkrecht aufeinander. Daraus folgt, dass der Körper seine (kinetische) Energie unverändert beibehält. Der Betrag der Geschwindigkeit ist also konstant. |
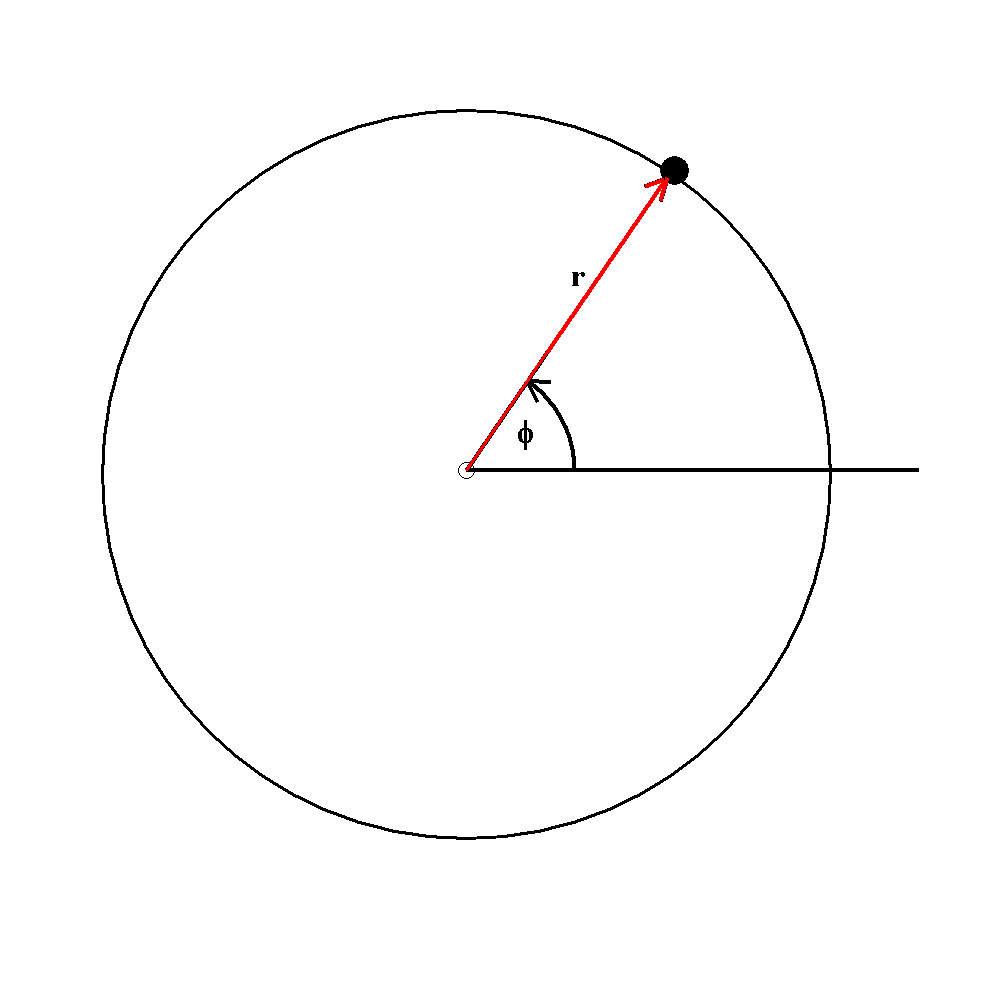 |
"Angepasste
Koordinaten" bei einer Kreisbewegung in einer Ebene.
Bei einer gleichförmigen Kreisbewegung sind diese besonders zweckmäßig, weil der Radius konstant ist. Man braucht dann also nur die Änderung der Winkelkoordinate φ betrachten. Für den Winkel φ und den Betrag der Bahngeschwindigkeit gilt dann: = ω·t , wobei ω die konstante Winkelgeschwindigkeit ω = /t ist v = r·Δφ/Δt = r·ω Für die Zentralbeschleunigung a findest du: a = v2/r = ω2·r Ganz entsprechend für die Zentralkraft ("Zentripetalkraft"): FZ = m·a = m·v2/r = m·ω2·r Der in der Abbildung gezeichnete Radiusvektor, der sich beim Umlauf mit dem Körper bewegt, heißt auch Fahrstrahl (rot). |
:
( September 2013)