Z.B. indem solche Wellen in einen Resonator eindringen und (möglichst verlustlos) mehrfach hin und her reflektiert werden, entstehen "stehende Wellen". Ein solcher Resonator könnte ein Seil sein, dessen eines Ende periodisch hin und her bewegt wird. Für das Entstehen von stehenden Wellen ist es egal, ob das andere Ende irgendwo befestigt ist oder nicht. Für die Resonanzfrequenz dagegen ist das sehr wichtig. Allgemein beobachtet man stehende Wellen, wenn sich zwei gegenläufige Wellen gleicher Wellenlänge (bzw. Frequenz) und gleicher Schwingungsrichtung "überlagern" (addieren). Stehende Wellen enthalten Energie, übertragen aber i.A. - anders als fortschreitende Wellen - weder Energie noch Impuls.

Abb. 1: Hier werden durch zwei Wellenzentren an den Enden des Federwurms gegenläufige Wellen erzeugt. Die Wellen überlagern (addieren) sich. Voraussetzung für das Entstehen von stehenden Wellen ist hier, dass beide Wellenzentren durch die Handbewegung mit der gleichen Frequenz schwingen, was im Foto noch nicht exakt erreicht ist. Wäre schon eine stehende Welle entstanden, gäbe es Punkte dauernder Ruhe, so genannte Knoten.

Da kannst es wie im Foto mit einem Federwurm oder auch mit einem Seil ausprobieren. Wenn du gleichmäßig "schüttelst" entstehen nur bei bestimmten Frequenzen regelmäßige und ortsfeste "Knoten" und "Bäuche" bei evtl.  riesigen Amplituden. Dann stimmt die Frequenz deiner Schüttelbewegung mit einer der Resonanzfrequenzen überein. Die Schüttelfrequenz heißt auch Erregerfrequenz (weil eine stehende Welle "erregt" oder "angeregt" wird), die Resonanzfrequenzen heißen auch "Eigenfrequenzen", weil sie dem Resonator oder schwingungsfähigem System "eigen" sind. Die Eigenfrequenzen hängen z.B. von der Seillänge ab, und ob das Seilende fest oder lose ist, vielfach auch von der Art der Energiezufuhr. Häufig besitzen Resonatoren mehrere verschiedene Resonanzfrequenzen.

Bei stehenden Wellen haben benachbarte Knoten den Abstand einer halben Wellenlänge λ/2. Du könntest mit dieser Kenntnis also die Wellenlänge messen. An der Stelle fester Enden müssen Knoten sein ¹. Das führt dazu, dass in einen Resonator der Länge ℓ eine ganze Zahl von halben Wellenlängen eingepasst werden kann (Methode "Einpassen von halben Wellenlängen").

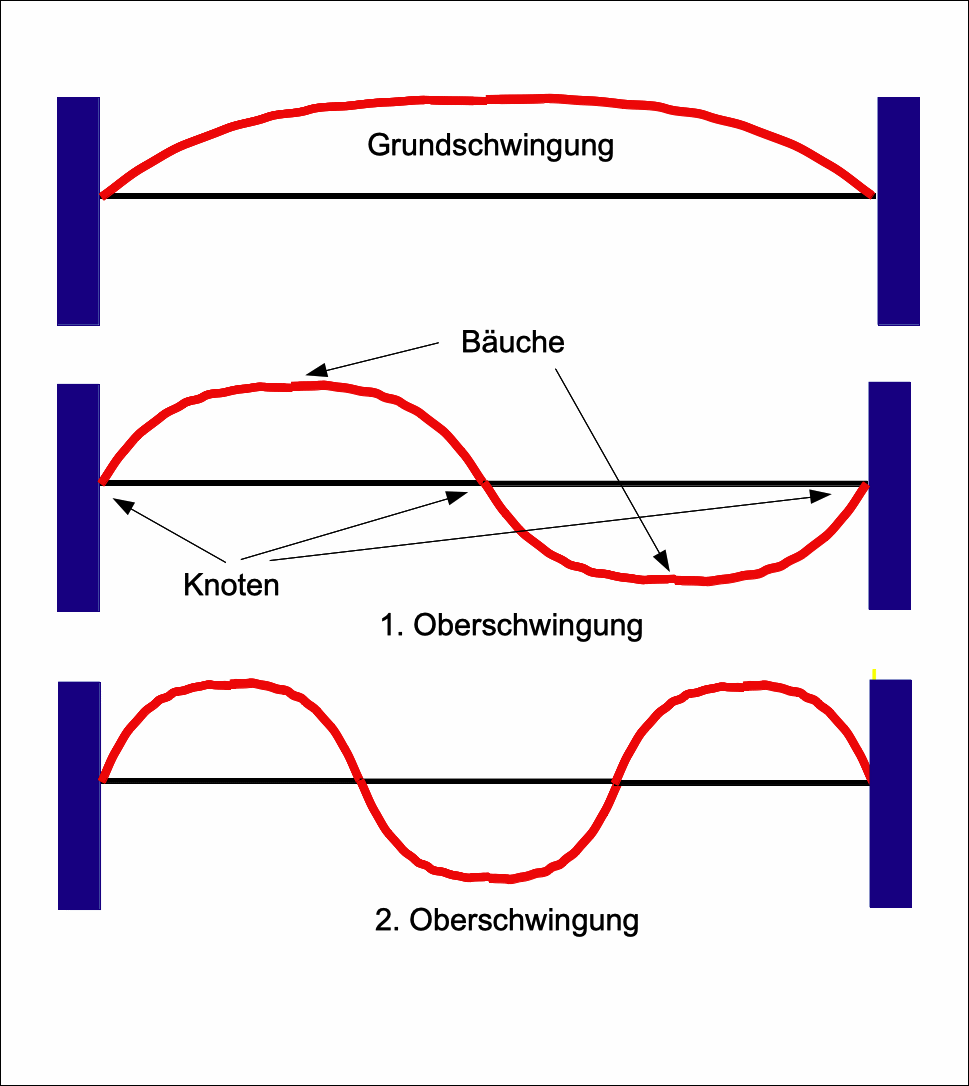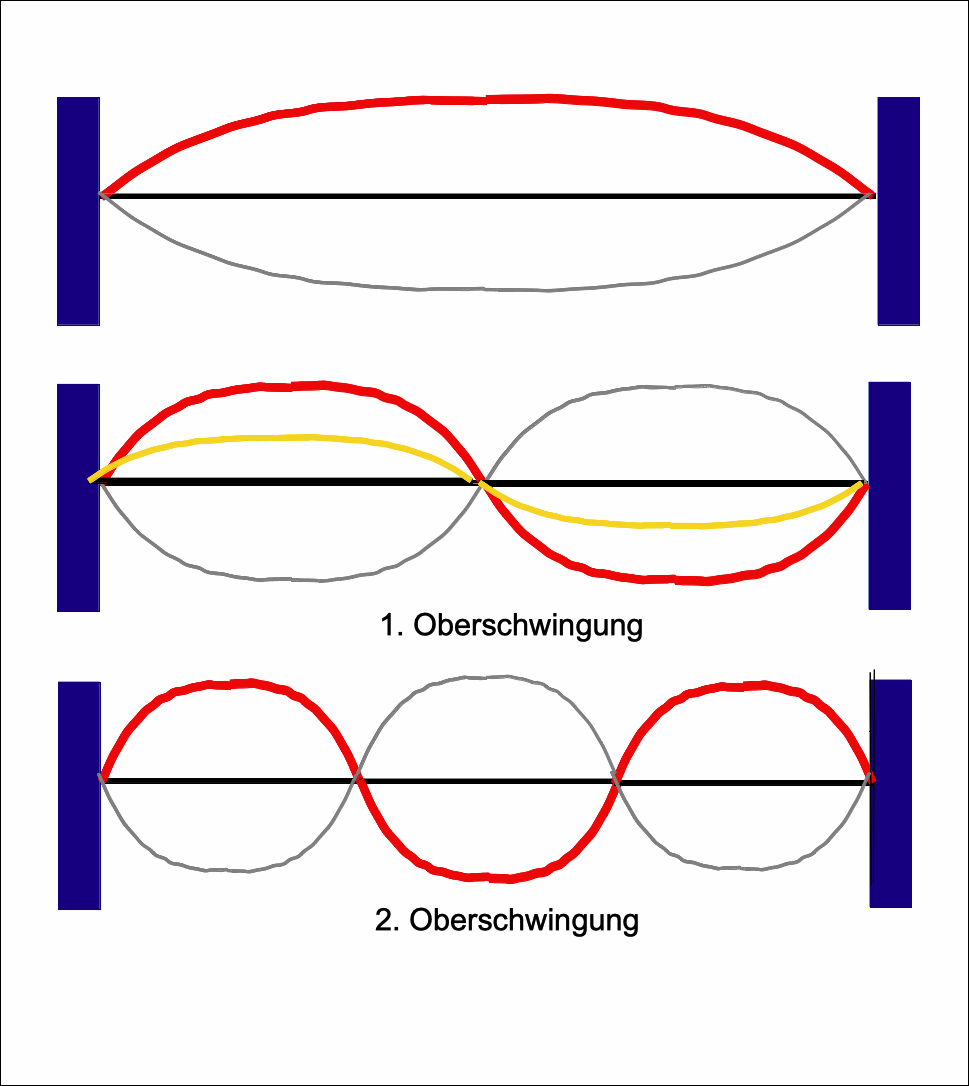
Abb. 2: Knoten und Bäuche bei stehenden Wellen. An den festen Enden links und rechts liegen Knoten. Die Zeichnung zeigt das "Einpassen von halben Wellenlängen" und Grund- und Oberschwingungen. Links: Momentaufnahme; Rechts: Momentaufnahmen zu den zwei Zeitpunkten extremaler Auslenkung. Zu anderen Zeiten wären Zwischenzustände erreicht (z.B. siehe Zeichnung der 1. Oberschwingung, gelb)

Du könntest so also die Wellenlänge λ bei einer der Resonanzschwingungen (Eigenschwingungen) festlegen. Mit der Kenntnis, dass Wellenlänge λ und Erregerfrequenz f mit der Ausbreitungsgeschwindigkeit c über λ·f = c zusammenhängen, könntest du die erforderliche Erregerfrequenz f ausrechnen, und mit T = 1/f die Zeit für eine volle Periode T deiner Handbewegung. Dann hättest du die Garantie, dass eine perfekte stehende Welle zustande kommt, ohne viel Probieren wie in Abb. 1.

Auch die Saiten einer Gitarre oder eines anderen Streichinstruments stellen Resonatoren dar. Ihre Eigenfrequenzen hängen von ihrer Länge ℓ, von ihrem Material (Nylon oder Stahl), ihrer Massenverteilung (dick oder dünn), und ihrer Spannung ab. Beim Stimmen verändert man die Spannung. Bei der Gitarre ändert der Musiker die Tonhöhe, indem er die Saite mit den Fingern auf einen Bund drückt und so den schwingungsfähigen Teil verkürzt.

Resonatoren für Schallwellen sind z.B. offene oder halbseitig geschlossene Röhren, Flaschen oder Orgelpfeifen. Das wird bei Musik-Instrumenten häufig genutzt zur Erzeugung von Tönen mit bestimmter Tonhöhe.

Auch Trommeln, Pauken oder "steel drums" sind Resonatoren mit ganz bestimmten Eigenfrequenzen.  "steel drums" aus der Karibik stellen eine Besonderheit dar. Sie sind aus Ölfässern gebastelt.

Stehende elektromagnetische Wellen werden im einfachsten Fall in quaderförmigen Hohlräumen mit sehr gut elektrisch leitenden Wänden erzeugt, an denen sie möglichst verlustlos hin und her reflektiert werden ("Hohlraumresonatoren").

Eine einfache Methode zur Untersuchung von stehenden Wellen bei beidseitig festen Enden besteht im "Einpassen von halben Wellenlängen"  λ/2 (Abb. 2). Betrachte etwa ein Seil der Länge ℓ. Du kannst n = 1, 2, 3, ... halbe Wellenlängen so einpassen, dass an den Enden jeweils ein Knoten liegt. Dementsprechend gilt λ/2·n = ℓ bzw. λ =  2·ℓ/n.

Beispiel: Bei einem Seil der Länge ℓ = 6 m soll vor dem Versuch die Periodendauer T für die Bewegung der Hand abgeschätzt werden. Die Wellenlänge für beliebiges n kennst du schon: λ = 12 m/n. Um auf Frequenz f und Periodendauer T zu kommen, brauchst du die Ausbreitungsgeschwindigkeit c, die von Seil zu Seil unterschiedlich ist. Du kannst sie mit einer einfachen Beobachtung abschätzen: Spanne das Seil wie beim eigentlichen Versuch und schlage dann mit dem Finger kräftig auf das Ende, quer zum Seil. Du siehst eine Störung längs des Seils laufen. Nehmen wir an, dass sie nach 1 s das Seilende erreicht. Dann gilt: c = 6m/1s = 6 m/s. Dann erhältst du f = c/λ = 6/12 1/s n und die Periodendauer T = 1/f = 2s / n . Für die Grundschwingung (n = 1) erhältst du also T = 1 s, für die 1. Oberschwingung (n =2) T = 0,5 s, usw.

Wenn ein Ende lose ist, musst du noch mit einer Viertel-Wellenlänge λ/4 korrigieren. Es gilt dann λ/2·n + λ/4 = ℓ (n = 0, 1, 2, ... ).

Wenn du verstehen möchtest, wie eine stehende Welle durch Reflexion an einem losen oder festen Ende zustande kommt, solltest du hier klicken.

¹ Das Ende, an dem Energie zugeführt wird, kann nur näherungsweise (trotz einer kleinen Öffnung) ein festes Ende sein, weil der Resonator andernfalls keine Energie aufnehmen könnte. Die in einer Periode zugeführte Energie kann gering sein im Vergleich zur gesamten Energie, die schließlich - nach vielen Perioden - in einem Resonator gespeichert ist.