Eine Stahlkugel oder ein Gummiball soll aus einer Höhe h auf eine horizontale elastische Platte fallen, von ihr reflektiert werden und wieder nach oben springen. Beim Aufprall soll jeweils 10 % der Energie "verloren gehen".

Eine beliebte Frage ist nach dem t-x-Diagramm bzw. dem t-s-Diagramm dabei, also die Frage, wie der Ort x der punktförmig angenommenen Kugel bzw. der von ihr zurück gelegte Weg s von der Zeit abhängt.

Es ist klar, dass die jeweiligen Orte x nur zwischen dem Startort und dem Reflexionsort auf der Platte variieren, also zwischen 0 und h. Auch ist klar, dass der zurückgelegte Weg s nach jeder Richtungsänderung weiter wächst. Ohne Energieverluste würde für jeden Abschnitt von oberem Umkehrpunkt über den Reflexionspunkt zum Wiedererreichen des oberen Umkehrpunkts jeweils der Weg 2·h zurückgelegt werden, bei n solchen Abschnitten also der Weg n·2·h (n = 1, 2, 3, ... ): der zurückgelegte Weg würde immer weiter anwachsen.

Weiter ist klar, dass bei dem Energieverlust von 10% bei jeder Reflexion die jeweils neu erreichte Höhe nur mehr 90% der vorausgehenden betragen kann.

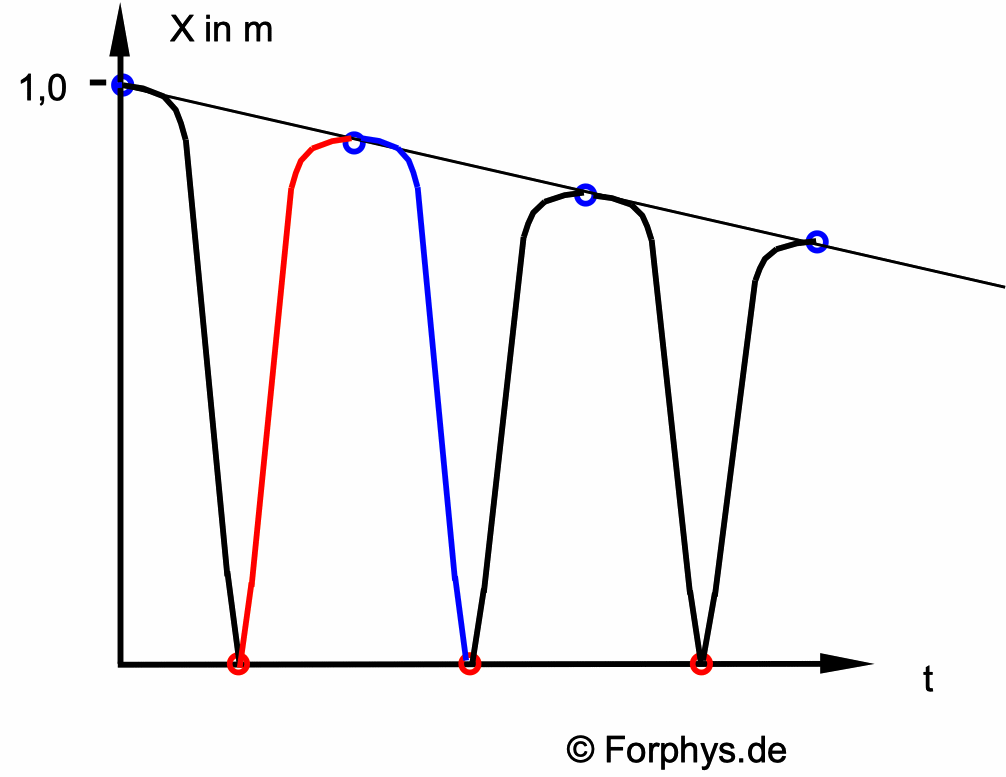
Abb. 1: Schematische Skizze des t-x-Diagramms der hüpfenden Kugel. Die jeweils 10%ige Abnahme der maximalen potenziellen Energie und damit der erneuten Steighöhe nach jeder Reflexion ist angedeutet. Wegen der konstanten Beschleunigung ist der Graph aus vielen Parabelstücken zusammengesetzt. Am Vorzeichen der Steigung des t-x-Graphen erkennst du Abschnitte mit positiver Geschwindigkeit (Aufwärtsbewegung; rot) und mit negativer Geschwindigkeit (Abwärtsbewegung; blau).

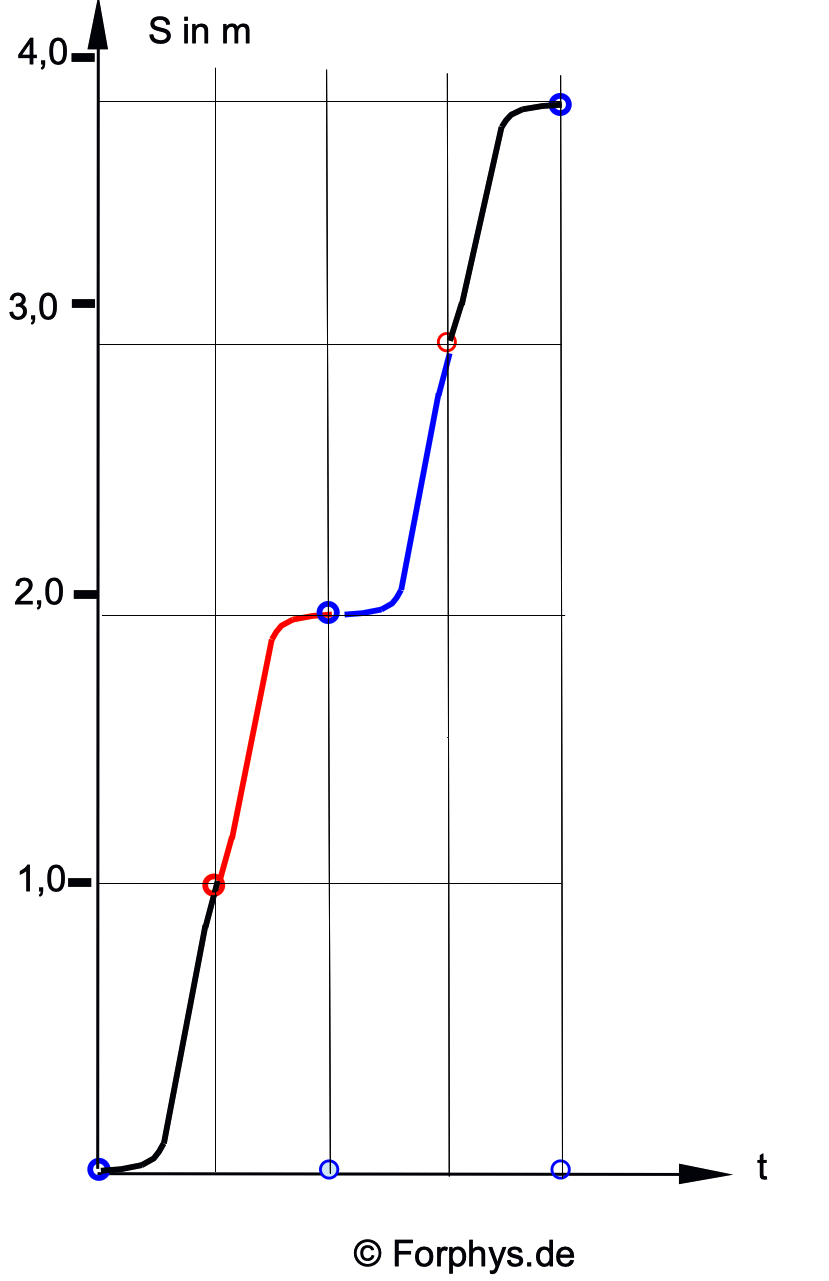Abb. 2: Schematische Skizze des t-s-Diagramms der Hüpfbewegung für zwei Perioden. Der zurückgelegte Weg seit Beginn der Bewegung wächst stets, unabhängig von der Bewegungsrichtung. Blau sind wieder die oberen Umkehrpunkte, rot die unteren Reflexionspunkte. Der zurückgelegte Weg s kann nie negativ sein und im Laufe der Zeit niemals kleiner werden. Aus der Steigung des t-s-Graphen kann man hier höchstens etwas über das Tempo ablesen, nicht über die Bewegungsrichtung und das Vorzeichen der Geschwindigkeit.

Hinweis: Hier wird sorgfältig zwischen Ort x und Weg s unterschieden. Es gibt auch Autoren, die von Weg s reden, aber Ort x meinen. Wenn sie nach dem t-s-Diagramm fragen, erwarten sie eine Antwort nach Abb. 1.