|
. . |
Physik für Schülerinnen und Schüler Die elektrische Spannung © H. Hübel Würzburg 2013 |
Empfohlene Glossarthemen: |
Impres-sum |
Das Kapitel über den Stromkreis solltest Du verstanden haben.
Die Spannung einer Stromquelle/Energiequelle
Auf den meisten Energiequellen ist die Spannung aufgedruckt, z.B. 1,5 V bei einer Monozelle, oder 4,5 V bei einer Flachbatterie oder 9 V bei einem 9V-Block. Das ist nur sinnvoll, wenn die Spannung mehr oder weniger konstant, typisch für die jeweilige Energiequelle ist. Wenn du ein 6 V-Lämpchen nacheinander an eine Monozelle und an eine Flachbatterie anschließt, folgerst du aus dem Leuchten, dass bei der größeren Spannung , bei der Flachbatterie also, ein stärkerer Strom fließt.
Eine Monozelle mit 1,5 V und eine Flachbatterie mit 4,5 V sind offenbar unterschiedlich "stark". Mit einem 9 V-Block solltest du den Versuch nicht durchführen. Dann wäre nämlich die Energiequelle so "stark", dass ein sehr großer Strom fließen würde, der das Lämpchen zerstören würde. Wie groß der Strom ist, den die Energiequelle durch einen Stromkreis pumpen kann, hängt nicht nur von ihrer "Pumpenstärke" ab, sondern auch noch vom Widerstand des Stromkreises.
Die Spannung einer Energiequelle ist eine Eigenschaft dieser Energiequelle allein, unabhängig davon, welcher Strom fließt und welche Ladung von der Energiequelle durch den Stromkreis, also vom Strom, transportiert wird. Auch, wenn überhaupt kein Strom fließt, besitzt die Energiequelle diese Spannung. *) Und du weißt auch, wie man eine solche Spannung mit einem Spannungsmesser misst. Man muss nämlich je einen Anschluss des Spannungsmessers mit dem Pluspol und dem Minuspol verbinden.
(Wenn du das ausprobieren möchtest, solltest du zuvor darauf achten, dass das Messgerät auf einen geeigneten Spannungsbereich eingestellt ist. Wäre es von einer früheren Messung noch auf den Strommessbereich eingestellt, würde das Messgerät, zumindest aber die eingebaute Sicherung, sofort durchbrennen.)
 |
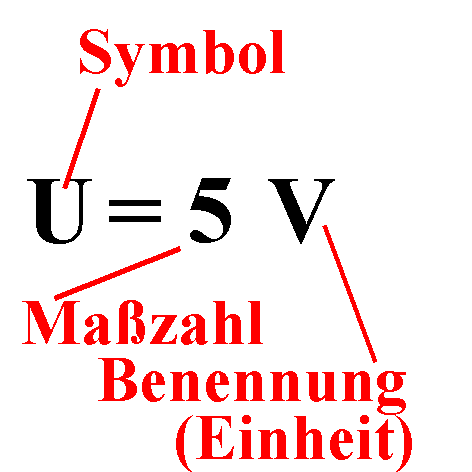
Als Symbol für die physikalische Größe Spannung hat man ein U eingeführt. Den Aufschriften auf Energiequellen entnimmst du, dass Spannungen in V (Volt) gemessen werden. Die Einheit der Spannung ist 1 V, V (Volt) ist die Benennung der Spannung. |
 |
Die beiden Mädchen führen einen Tanz zur Veranschaulichung von
Strom und Spannung auf. Hier also die Spannung, die immer zwischen
zwei Punkten gemessen wird. Es wurde im Fall der Spannung ein sehr ruhiger Tanz! (Vgl. den Stromtanz) |
| Die Spannung einer Energiequelle ist ein Maß für ihre "Pumpenstärke". |
"Pumpenstärke" ist kein offizieller Begriff. Er kennzeichnet aber meines Erachtens ganz gut, was man sich unter der Spannung einer Energiequelle vorstellen kann: Je größer die "Pumpenstärke" (Spannung U) einer Energiequelle ist, desto größer ist der Strom, den sie durch einen gegebenen Stromkreis hindurch pumpen kann.
Stromarbeit im elektrischen Stromkreis
Wenn beim Stromkreis die transportierte Energie eine so große Bedeutung hat, sollten wir sie etwas besser in den Griff bekommen. Vielleicht kennst du die Sprüche "Energie ist gespeicherte Arbeit" oder auch "Energie kennzeichnet die Fähigkeit erneut Arbeit zu verrichten". Damit wurde dir vielleicht ein plausibles Verständnis des Energiebegriffs vermittelt.
Jetzt aber zum Stromkreis: Betrachten wir einmal eine positive Ladung. Mittels der Energiequelle kann eine solche Ladung Q von einem Anschluss des Energiewandlers (z.B. des Lämpchens) bis zum anderen Anschluss hindurch gepumpt werden. Das geht in der Regel nicht von allein. Dazu ist eine Arbeit W nötig. Was geschieht mit ihr? Der Energiewandler erwärmt sich daraufhin und gibt Wärme oder Licht nach außen ab, oder er kann - im Falle eines Elektromotors - mechanische Arbeit verrichten.
Allgemeine Definition der Spannung zwischen 2 Punkten A und B **)
Es ist plausibel: Wenn die doppelte (dreifache, ... ) Ladung Q durch den Energiewandler hindurch gepresst werden soll, wird auch die doppelte (dreifache, ... ) Arbeit verrichtet werden (bei sonst gleichen Bedingungen). Dann ist also die verrichtete Arbeit zur Ladungsmenge Q proportional. Das heißt aber auch, dass der Quotient W/Q (Arbeit pro Ladungsmenge) unabhängig von der transportierten Ladung ist, wie die Spannung der Energiequelle auch.
Ein Energiewandler, der dem gleichen Stromfluss einen größeren Widerstand entgegensetzt, erfordert aber mehr Arbeit, also auch mehr Arbeit pro Ladungsmenge W/Q. Das schafft eventuell nur eine Energiequelle mit einer größeren Spannung U. Man hat deshalb auch dem Quotienten W/Q, also der Arbeit pro Ladungsmenge, einen Namen gegeben, nämlich "Spannung". Für den Fall, dass der Energiewandler der einzige Teil des Stromkreises ist, an dem die Energiequelle Arbeit verrichtet, stimmt die Arbeit pro Ladungsmenge auch zahlenmäßig mit Spannung der Energiequelle überein.
Für diesen Fall haben wir also eine neue Deutung der Spannung U.
(1) Die Spannung U einer Energiequelle ist einerseits eine Eigenschaft der Energiequelle, sozusagen ein Maß für ihre "Pumpenstärke".
(2) Andererseits ist die Spannung U zwischen 2 Punkten A und B diejenige Arbeit pro Ladungsmenge, die zum Transport dieser Ladung zwischen den Punkten A und B verrichtet werden muss**). Und in wichtigen Fällen (oder einer wichtigen Näherung) stimmen beide Spannungsbegriffe sogar überein. Wenn es um Spannung als Eigenschaft der Energiequelle geht, sind dann die Punkte A und B die beiden Pole der Energiequelle. (2) ist also der allgemeinere Spannungsbegriff, der auch im Fall (1) und in allen anderen Fällen anwendbar ist.
Wenn zwischen 2 Punkten A und B also eine Spannung U herrscht und wenn die beiden Punkte durch einen Leiter verbunden werden, dann bewirkt U, dass ein Strom zwischen beiden Punkten fließt. ("Spannung macht Strom")
Wenn die beiden Punkte nicht durch einen Leiter verbunden sind, kann auch kein Strom fließen. Dann ist U = W/Q immer noch durch die Arbeit definiert, die man aufwenden müsste, um eine Ladung Q von dem einen zum anderen Punkt zu verschieben.
Diese verallgemeinerte Spannungsdefinition hat weitreichende Folgen:
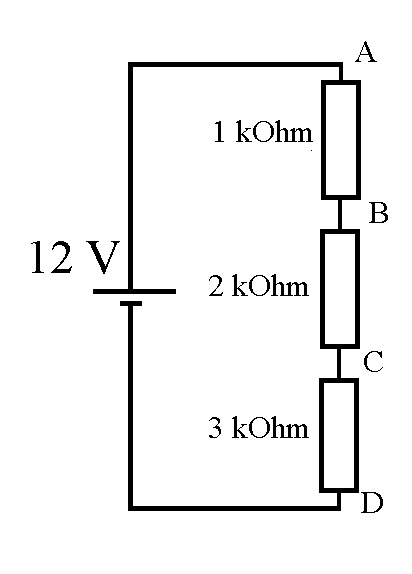 |
Durch die drei in Reihe geschalteten Widerstände fließt ein
Strom. Wenn das der Fall ist, kannst du zwischen je zwei der
markierten Punkte eine Spannung messen. Probier das aus! Für die
Spannung zwischen B und C ergibt sich z.B. 4 V. Man nennt das den
Spannungsabfall an einem Widerstand, wenn dieser von einem
Strom durchflossen wird.
Ganz klar: Zum Transport einer Ladung Q von B nach C muss die Energiequelle eine Stromarbeit W verrichten. Aus UBC = W/Q ergibt sich der Spannungsabfall UBC . Später wirst du erfahren, wie er leicht berechnet werden kann. Hier ist es so, dass zum Transport derselben Ladung von B nach C doppelt so viel Arbeit verrichtet werden muss wie für den Transport von A nach B. Für den Transport von C nach D muss sogar dreimal so viel Arbeit verrichtet werden. Dementsprechend ist die Spannung zwischen B und C doppelt so groß wie die Spannung zwischen A und B, die Spannung zwischen C und D sogar dreimal so groß. Miss es nach!
|
| Eine Spannung wird immer zwischen zwei Punkten gemessen,
die Spannung der Energiequelle also zwischen ihren beiden
Polen. Die Spannung zwischen zwei beliebigen Punkten A und B wird
eben zwischen diesen beiden Punkten gemessen.
Spannung zwischen zwei Punkten A und B ist diejenige Arbeit pro Ladungsmenge Q, die zum Transport dieser Ladung Q zwischen den Punkten A und B vom Strom verrichtet werden muss:
|
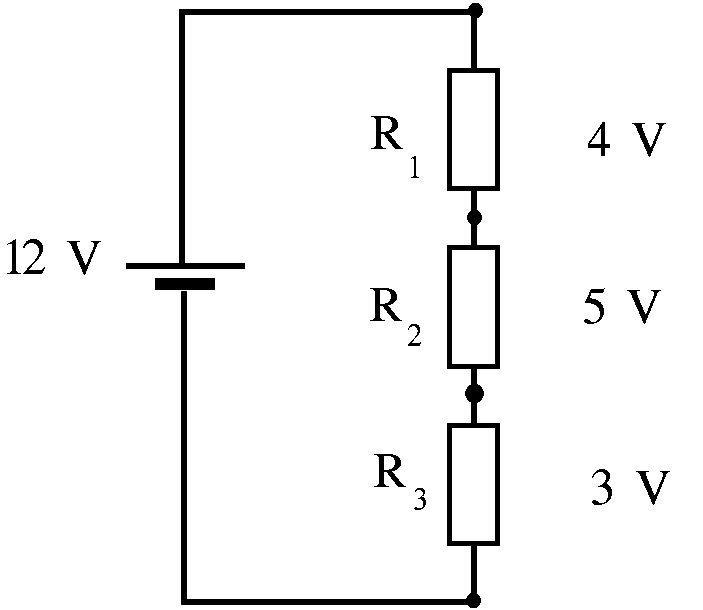 |
Wenn bei einer Kette von Widerständen einer herausgezogen wird,
z.B. R2, bricht mit dem Strom sofort jeder
Spannungsabfall an jedem Widerstand zusammen. Die Spannungen an R1
und R3 werden dann 0 V, die Spannung zwischen den
früheren Anschlüssen von R2 ist dann die volle
Spannung 12 V. Probier's aus!
Klar, denn ohne Strom wird ja auch keine Arbeit verrichtet, um den Strom durch einen Widerstand hindurch zu pressen. Der Spannungsabfall zwischen zwei Punkten A und B ist Arbeit pro Ladungsmenge Q für den Transport der Ladung zwischen den Punkten A und B. Und die genannten 12 V sind gerade die Spannung der Energiequelle. Wenn zwischen zwei Punkten A und B ein Strom fließt, obwohl zwischen beiden Punkten ein Widerstand liegt, muss zwischen beiden Punkten eine Spannung U entstehen ("Strom macht Spannung"). (Widerstände hier anders als im letzten Bild) |
( Einfluss vom Verlauf des Weges zwischen den beiden Punkten (Diesen Abschnitt könntest du zunächst einmal übergehen)
In einigen wichtigen Fällen (I) kommt es auf den Verlauf des Wegs zwischen den beiden Punkten A und B nicht an. Das ist in der Elektrostatik immer der Fall. Zwischen zwei Punkten A und B wird immer die gleiche Spannung U gemessen, ganz gleich auf welchem Weg die Anschlüsse von A und B zum Spannungsmesser führen.
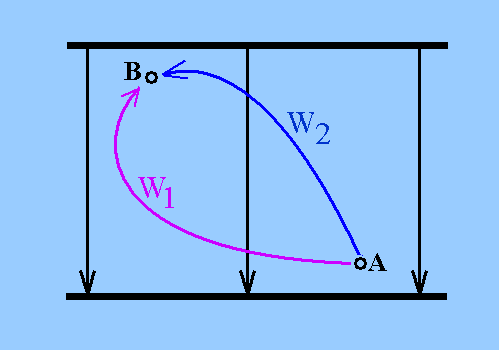 |
Fall I (z.B. bei einer Ladung im Plattenkondensator): Zwischen
den beiden Punkten A und B wird immer die gleiche Spannung
gemessen, ganz gleich wie der Weg zwischen den Punkten verläuft.
Transportiert man die Ladung Q auf dem einen Weg von A nach B und
dann auf einem anderen Weg von B nach A zurück, wird insgesamt
keine Arbeit verrichtet. Die Arbeit, die auf einem Teilweg
verrichtet werden muss, wird auf dem anderen Teilweg wieder
gewonnen. Das gilt so in der Elektrostatik.
(Hier handelt es sich um einen Plattenkondensator mit horizontal verlaufenden Platten. Die Pfeile deuten die Richtung des elektrischen Feldes an. Die beiden Arbeiten W1 und W2 für den Transport einer Ladung von A nach B sind unabhängig vom Weg immer gleich. Die Messung der Spannung zwischen A und B ist allerdings nicht ganz so einfach.) |
In einigen anderen wichtigen Fällen (II) kommt es auf den Verlauf des Wegs zwischen den beiden Punkten A und B sehr wohl an. Dazu gehört z.B. die Spannung bei der elektromagnetischen Induktion. Grob gesagt hängt dort die Spannung zwischen beiden Punkten davon ab, ob der Weg zwischen A und B ein sich änderndes Magnetfeld einschließt oder nicht. Das wirst du später genauer untersuchen.
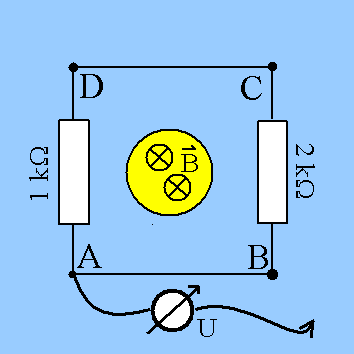 |
Fall II (z.B. bei der elektromagnetischen Induktion): Zwischen
den beiden Punkten A und D (oder C) werden unterschiedliche
Spannungen gemessen, je nachdem, wie der Weg zwischen den Punkten
verläuft. Transportiert man die Ladung Q auf dem direkten Weg von
A nach D (über den Widerstand 1 kOhm) und dann auf einem anderen
Weg über C und B nach A zurück (also über den 2 kOhm-Widerstand),
wird insgesamt eine Arbeit verrichtet oder gewonnen. Die Arbeit,
die auf einem Teilweg verrichtet werden muss, ist verschieden von
der Arbeit auf dem anderen Teilweg. Das ist z.B. bei der Induktion
der Fall, wenn der geschlossene Weg von A über D, C und B
nach A ein sich zeitlich änderndes Magnetfeld einschließt.
Der gelbe Bereich ist hier ein Bereich mit einem sich zeitlich ändernden Magnetfeld. Die Spannung UAC ist dann doppelt so groß wie die Spannung UAD (direkter Weg). Das wirst du in einem späteren Schuljahr genauer verstehen. Wenn das Magnetfeld sich nicht zeitlich ändert, sind natürlich beide Spannungen gleich groß, nämlich 0. |
Die beiden Punkte A und B könnten in jedem Fall sogar zusammenfallen. Das erscheint zunächst ziemlich witzlos. Denn wenn die Spannung nicht vom Verlauf des Wegs von A nach B ( = A) abhängt - wie im Fall (I), kann man ja auch den kürzesten Weg von A nach A wählen (also keinen) und erhält trotzdem das gleiche Ergebnis, nämlich U = 0 V. Aber im Fall (II) könnte einerseits der gleiche kürzeste Weg gewählt werden; man würde auch 0 V erhalten. Oder es könnte ein Weg von A nach A gewählt werden, der ein sich änderndes Magnetfeld ganz einschließt. Dann könnte man eine von 0 V verschiedene Spannung erhalten. Eine solche Spannung (von A nach A) heißt häufig Ringspannung. Damit brauchst du dich jetzt aber nicht weiter herumschlagen, weil du es später genauer kennen lernen wirst. Die Bemerkung hier soll nur ein Warnschild aufstellen: "Vorsicht! Achte bei der Spannung auf den Weg!" )
Folgerungen für Stromarbeit W und Leistung P
Wenn U = W/Q die Spannung ist, die zwischen zwei Punkten A und B (z.B. den Anschlüssen eines Widerstands) herrscht, kann man damit die Arbeit W leicht berechnen, die beim Transport der Ladung Q verrichtet wird:
| W = U·Q |
Diese Arbeit wird in der Regel zum größten Teil nach außen abgegeben. Nehmen wir ein Beispiel: An einem Widerstand liegt die Spannung 230 V. Durch ihn soll ein Strom mit der Stromstärke I = 0,40 A fließen. Dann fließt in 10,0 s eine Ladungsmenge Q = I·t = 0,40 · 10,0 A·s = 4 C hindurch. In diesen 10 s wird also die Arbeit W = U·Q = 230 V· 4 C = 920 V·C = 920 V·A·s verrichtet. Aber eine übliche Einheit der Arbeit (wie auch der Energie) ist doch 1 J (Joule)?
Stell dir vor, der Widerstand wäre ein Tauchsieder, der in einem gut isolierten Gefäß 1 l Wasser erwärmt. Dann könntest du durch die Erwärmung von 1 kg Wasser leicht die verrichtete Arbeit in J (Joule) messen. (Alle Arbeit wird hier in "Wärme" (= "innere Energie") umgewandelt.) Dann bestätigt sich deine Vermutung: Das Wasser nimmt 920 "Wärme" auf; die oben berechnete Arbeit beträgt also ebenfalls 920 J, und du musst dir merken:
| [W] = 1 J = 1 V·A·s |
(Die eckigen Klammern bedeuten "Einheit von". [W] bedeutet also die Einheit der Arbeit W.)
Daraus ergibt sich dann automatisch die Einheit der Leistung P:
| [P] = 1 W (Watt) = 1 J/s = 1 V·A |
Zur Wiederholung: Leistung P ist Arbeit pro Zeiteinheit, also P = W/t. Wird in 1 s die Arbeit 1 J verrichtet, beträgt die Arbeit 1 J/s = 1 W (Watt). 60 W - typisch für eine Haushalts-Glühbirne - bedeutet dann, dass in 1 s die Stromarbeit 60 J verrichtet wird.
Braucht man immer eine Spannung, damit ein Strom fließt?
Die Frage kannst du selbst beantworten, wenn du von der Definition der Spannung ausgehst. Zunächst scheint das so zu sein: Du dürftest bisher kaum mit einer anderen Situation in Berührung gekommen sein. Denn alle Stromkreise, die du kennst, enthalten einen Widerstand. Und wozu braucht man eine Spannung? Damit die Energie, die durch einen Widerstand nach außen abgegeben wird, wieder ersetzt wird, ersetzt wird durch Stromarbeit (bzw. elektromagnetische Energie). Und Spannung ist Stromarbeit pro Ladungsmenge beim Transport dieser Ladungsmenge. Also ganz klar:
| In einem Stromkreis mit einem Widerstand kann kein dauernder Strom fließen ohne eine Spannung. |
Aber, wenn kein Widerstand im Stromkreis ist? Wäre in einem solchen Stromkreis auch eine Energiequelle eingebaut, würde eine Katastrophe passieren: Da kein Widerstand den Strom begrenzt, würde der riesige Strom infolge des Kurzschlusses schnell die Energiequelle und die Leitungen zerstören.
Andererseits, wenn zwischen zwei Punkten A und B im Stromkreis kein Widerstand liegt, wird auch keine Stromarbeit beim Transport einer Ladung verrichtet. Dann braucht man also keine Spannung.
Widerstandslose Materialien wurden 1911 von dem Holländer Kamerlingh-Onnes entdeckt, so genannte Supraleiter. Kühlt man ein solches Metall unter eine bestimmte Temperatur ab, verliert es jeden noch so kleinen Widerstand. (Diese Temperatur liegt nahe beim absoluten Temperaturnullpunkt, aber bei Hochtemperatur-Supraleitern deutlich höher). Wenn in einem solchen Stromkreis ohne Energiequelle ein Strom irgendwie zustande kommt, dann kann er jahrelang verlustlos im Stromkreis fließen.
| In einem Stromkreis ohne Widerstand (mit supraleitenden Verbindungen) kann ein dauernder Strom jahrelang ohne Spannung fließen. |
Du kannst die Verhältnisse im elektrischen Stromkreis jetzt also so beschreiben:
(I) Der elektrische Strom verrichtet an einem Widerstand, einem Lämpchen oder einem Elektromotor, allgemein einem Energiewandler, Stromarbeit. Sie wird ganz in Energie anderer Energieformen umgewandelt, die i.A. nach außen abgegeben werden. Möchte man die Spannung an dem Energiewandler ("zwischen den Enden /Anschlüssen des Energiewandlers") messen, braucht man also nur die Ladung Q kennen und die Arbeit W beim Transport dieser Ladung Q von einem Anschluss des Energiewandlers zum anderen. Dann gilt: U = W/Q
Was ermöglicht es aber dem elektrischen Strom diese Stromarbeit zu verrichten, und wie geschieht das? Das ist in vielen Fällen völlig uninteressant und wird in der Regel offen gelassen. Es ist aber wohl bekannt.
(II) Du könntest aber auch so argumentieren: Aus der Energiequelle fließt elektromagnetische Energie, "wenn ein Energiewandler sie benötigt, und soviel er benötigt". Sie ermöglicht es, dass Stromarbeit verrichtet wird. Stromarbeit wird in Energie anderer Energieformen umgewandelt, die damit letzten Endes aus der elektromagnetischen Energie von der Energiequelle her kommt. Das funktioniert ganz offensichtlich nur, wenn auch ein Strom fließt.
Aufgabe:
Ein kleineres Fluss-Kraftwerk liefert in 1 s die Energie 10 MJ an die Haushalte der benachbarten Stadt. Wieviel Energie liefert es, wenn durch einen Störfall sämtliche Sicherungen in der Stadt "durchgebrannt" sind?
1. Zwischen zwei Punkten A und B herrscht eine Spannung U. 2. Die Stromquelle/Energiequelle besitzt eine Spannung U. 3. Am Punkt B herrscht im Vergleich zum Punkt A eine Spannung U. 4. Am Energiewandler (Widerstand, Lämpchen, ... ) liegt eine Spannung U. |
Hinweise:
1. Die Definition der Spannung, wie sie hier dargestellt ist, entspricht der offiziellen Definition. Sie ist z.B. für industrielle Anwender durch die DIN-Norm 1324 gesetzlich vorgeschrieben. Wenn du sie irgendwo nachlesen würdest, käme dir der Wortlaut allerdings etwas spanisch vor. Erst in einem späteren Schuljahr kannst du verstehen, dass der Wortlaut dort den Erklärungen hier entspricht.
2. Lass' dich nicht durch bestimmte Schulbücher verwirren, die eine Spannung allgemein mit Begriffen wie Trennarbeit oder potenzieller Energie definieren wollen. In einigen - meiner Meinung nach eher seltenen Fällen - kommt dabei sogar die richtige Spannung heraus. Im allgemeinen ist das aber nicht der Fall und es besteht die Gefahr, dass sich dir so Fehlvorstellungen einprägen, z.B. im Zusammenhang mit der Induktion, die du später kennen lernen wirst.
*) Dass es hier einen häufig kleinen Unterschied zwischen der "Quellenspannung" und der "Klemmenspannung" gibt, soll hier vernachlässigt und nicht weiter diskutiert werden.
**) Genau genommen ist der Begriff "Spannung U zwischen 2 Punkten A und B" zu ungenau, weil das Vorzeichen der Spannung nicht berücksichtigt wird. Man müsste also eine "Spannung am Punkt B im Vergleich zum Punkt A" definieren. Für den Anfangsunterricht wurde das übergangen. Es ließe sich leicht in die Ausführungen hier einbauen. ( zurück)