·

Die spezielle Relativitätstheorie Einsteins (1905) macht Aussagen darüber, wie Vorgänge in unterschiedlichen Bezugssystemen beschrieben werden müssen, die im Vergleich zueinander ("relativ zueinander") gleichförmig bewegt sind. Damit ist die Bedeutung des Wortteils "Relativität" erklärt. Der Name hat nichts mit allgemeineren Aussagen zu, dass etwa "alles relativ" sei, dass es etwa keine festen Wahrheiten geben könne. Eine solche Verallgemeinerung, die nach Einstein von Nichtphysikern manchmal gemacht wurden, hat mit der physikalischen Relativitätstheorie nicht zu tun.

1. Die (Vakuum-)Lichtgeschwindigkeit als Grenzgeschwindigkeit für die Ausbreitung von Teilchen und Nachrichten

Die Physiker Kaufmann (1901) und Bucherer (1909) führten bereits früh Experimente mit schnellen Elektronen durch. Sie verwendeten ß-Teilchen, die beim radioaktiven Zerfall entstehen, also sehr schnelle Elektronen. Sie ließen sie durch ein Wien'sches Geschwindigkeitsfilter laufen. Von den durchtretenden Elektronen kannten sie dann die Geschwindigkeit. Anschließend liefen die Elektronen auf einer Kreisbahn durch ein reines Magnetfeld. Aus dem Bahnradius ermittelten sie den Elektronenimpuls p = e·r·B und erhielten damit eine Darstellung, wie der Impuls p von der Geschwindigkeit v abhängt. Nach der klassischen Mechanik sollten beide Größen zueinander proportional sein. Die Messkurve zeigt ein anderes Ergebnis.

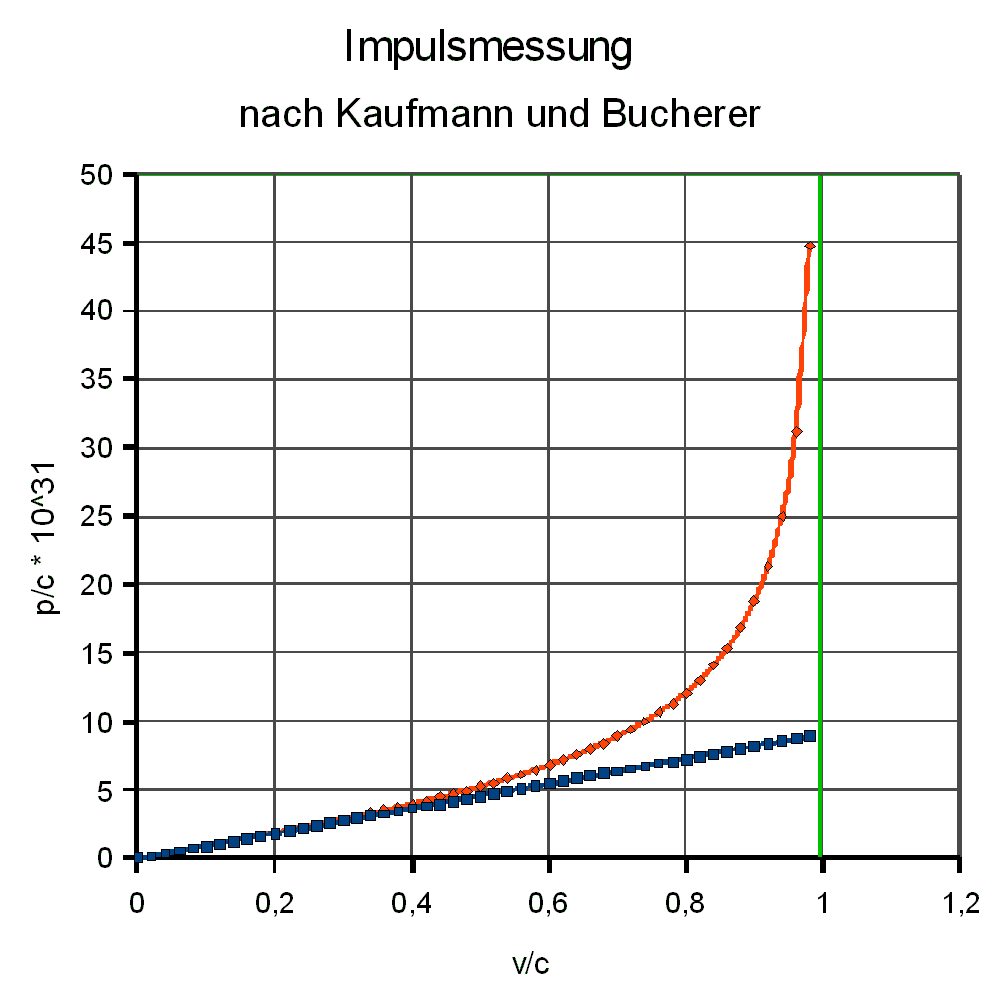Blau: klassischer Impuls p = m·v: p und v sind proportional zueinander. Rot: gemessener relativistischer Impuls: p und v nicht nicht proportional. Ergebnis: 1. Offenbar stellt die Lichtgeschwindigkeit (v/c = 1) eine Asymptote dar (grün). In Realität können die Elektronengeschwindigkeiten diesen Wert nicht überschreiten. 2. Die klassische Impuls-Geschwindigkeits-Beziehung kann nicht mehr gelten; Geschwindigkeit und Impuls sind nicht mehr proportional zueinander. 3. Wenn sich die Teilchengeschwindigkeit v nur geringfügig weiter an die Lichtgeschwindigkeit annähert, wächst der Impuls extrem stark an. Oder umgekehrt: Man muss den Impuls gewaltig ändern, um die Geschwindigkeit noch ein wenig näher an die Lichtgeschwindigkeit heran zu bringen.

Bei einem etwas neueren Versuch beschleunigten Bertozzi und Mitarbeiter (1962) Elektronen aus einer Elektronenquelle durch eine Hochspannung bis in den MeV-Bereich (15 MeV). Anschließend ließen sie die Elektronen durch eine lange evakuierte Röhre laufen. Die kinetische Energie erhielten sie aus der Beschleunigungsspannung. Die Geschwindigkeit v maßen sie durch die Laufzeit zwischen zwei Sensoren. (Wenn die Teilchen mit Lichtgeschwindigkeit liefen, bräuchten sie für die Entfernung von 9 m die unvorstellbar kurze Zeit von 3·10^-8 s; es mussten also extreme Kurzzeituhren verwendet werden). Wenn gelten würde E_kin = m/2 v² müsste die Geschwindigkeit gemäß v = √(2·E_kin /m ) von der kinetischen Energie abhängen. Man bräuchte dann nur die kinetische Energie genügend zu erhöhen um jede beliebige Geschwindigkeit zu erreichen. Das Experiment zeigt aber: Trotz zunehmender kinetischer Energie kann die Geschwindigkeit nie einen bestimmten Grenzwert, die Vakuumlichtgeschwindigkeit c = 3·10⁸ m/s, überschreiten, ja sie sogar nie erreichen.

Du kannst dir das Experiment im Video anschauen: http://education.jlab.org/scienceseries/ultimate_speed.html

Was haben Elektronen mit Licht zu tun? Nichts! Hier versteckt sich stattdessen etwas ganz Grundsätzliches.

Ähnliche Experimente werden heutzutage an den großen Beschleunigeranlagen auf der ganzen Welt, wie in Hamburg bei DESY, oder nahe bei Genf, beim CERN, täglich millionenfach mit noch viel größeren Energien bestätigt. Kein Teilchen mit Masse kann jemals die (Vakuum-)Lichtgeschwindigkeit erreichen.

Es gibt Teilchen mit einer sehr kleinen Masse, die Neutrinos. Ihre Masse ist größenordnungsmäßig 100 000 mal kleiner als die des schon sehr leichten Elektrons. Sie bewegen sich schon bei einer geringen Energie fast mit Lichtgeschwindigkeit, so dass man bis vor wenigen Jahrzehnten angenommen hat, sie hätten überhaupt keine Masse und bewegten sich immer mit Lichtgeschwindigkeit. Wenn in den großen Beschleunigeranlagen Protonen beschleunigt werden, die (in Ruhe) eine ca. 2000 mal größere Masse als ein Elektron haben, muss man ihnen schon sehr große Energie zuführen, damit sie mit der Lichtgeschwindigkeit vergleichbare Geschwindigkeiten erreichen.

Tabelle mit Beispielen zum Größenvergleich

Teilchen (Ruhe-)Masse Ruheenergie kinetische Energie Geschwindigkeit Elektron 9,1·10-31 kg 0,511 MeV 5,1 keV 0,14·c Neutrino <  4.10-39 kg < 0,2 eV (Stand 2011) 1 eV fast c Proton 1,67·10-27 kg 938 MeV 94 MeV 0,14·c C-Kern (Kohlenstoff) 2,0·10-26 kg 18,76 GeV 1,88 GeV 0,14·c

......

1 keV 1000 eV 1 MeV 106 eV 1 GeV 109 eV 1 eV = 1,6·10-19 J

Bei der Ausbreitung von Lichtwellen durch Materie muss man zwischen mehreren Geschwindigkeiten unterscheiden: der Phasengeschwindigkeit, der Frontgeschwindigkeit und der Gruppengeschwindigkeit. Die Phasengeschwindigkeit ist die Geschwindigkeit mit der sich eine bestimmte Wellenphase (z.B. der "Nulldurchgang") ausbreitet (sie heißt in der Schule häufig "Ausbreitungsgeschwindigkeit"). Man kann sich vorstellen, dass sie in Materie dadurch zustande kommt, dass Licht von Atomen absorbiert und phasengerecht wieder emittiert wird, wobei aber ein Phasensprung vorwärts oder rückwärts entstehen kann. Deshalb kann die Phasengeschwindigkeit größer oder kleiner als die Vakuum-Lichtgeschwindigkeit sein. Wie das ist, hängt von den Atomen und der Struktur der Materie ab. Mit der Phasengeschwindigkeit können aber keine Nachrichten übertragen werden. Für die Ausbreitung von Wellenpaketen ("Wellengruppen") und Teilchen ist die Gruppengeschwindigkeit v_g zuständig. Die Frontgeschwindigkeit von elektromagnetischen Wellen (Licht) ist in jedem Medium, nicht nur im Vakuum, gleich der Vakuum-Lichtgeschwindigkeit. Nur, wenn der Brechungsindex in Materie nicht von der Wellenlänge abhängt, stimmen die drei Geschwindigkeiten überein. Ist das nicht der Fall, spricht man von "Dispersion".

Die Aussage der RT bezieht sich also auf die Gruppengeschwindigkeit. Sie ist die ultimative Grenzgeschwindigkeit für Teilchen und Nachrichten (Informationen).

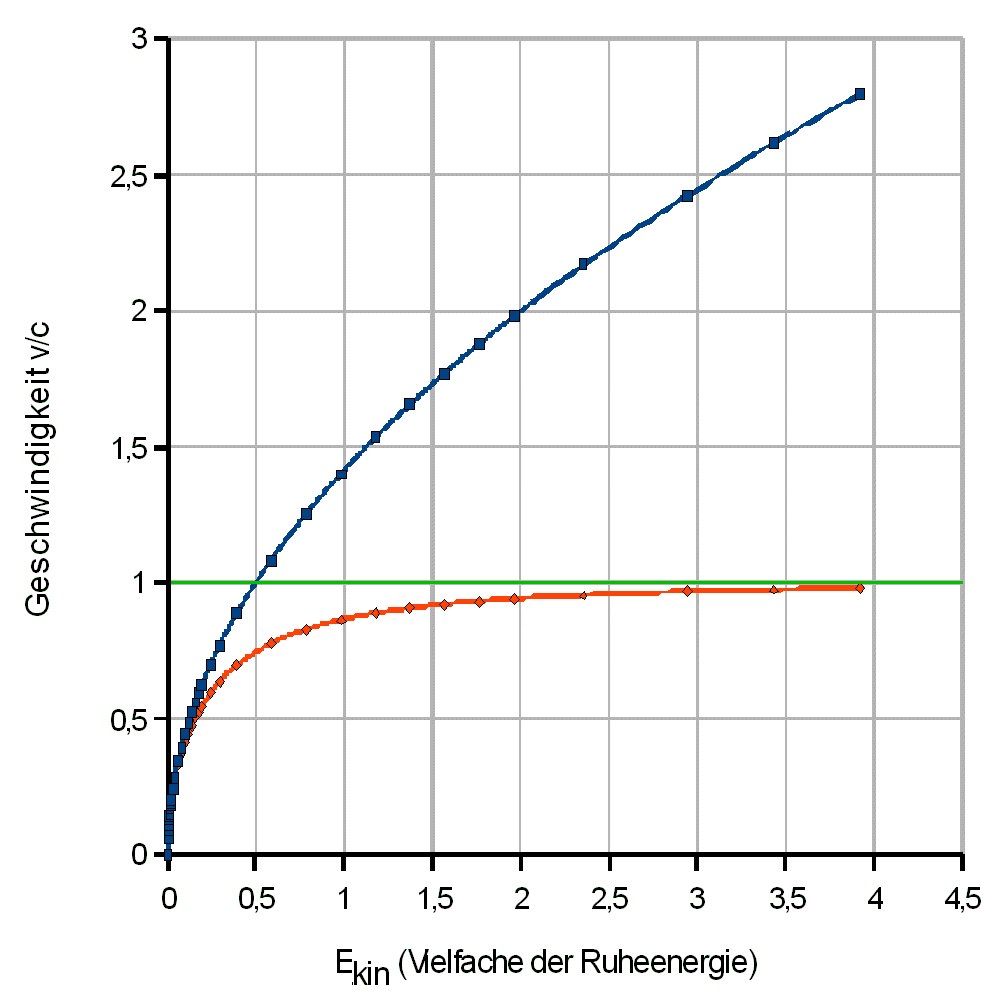Der Bertozzi-Versuch Ergebnis: 1. Die Elektronengeschwindigkeit kann eine bestimmte Grenzgeschwindigkeit, die Vakuum-Lichtgeschwindigkeit c (grün), weder erreichen noch überschreiten. 2. Trotz deutlicher Zunahme der kinetischen Energie ändert sich die Geschwindigkeit v bei Annäherung an die Vakuum-Lichtgeschwindigkeit c nur noch wenig. Blau: nach klassischer Physik Rot:  nach Messung

Tscherenkov-Effekt

Du hast vielleicht schon einmal Fotos von einem Abklingbecken in einem Kernkraftwerk gesehen. Dort werden abgebrannte Brennstäbe aus dem Reaktor nach dem Entfernen aus dem Reaktorkern monatelang in Wasser gelagert, bis die stärkste Radioaktivität abgeklungen ist. Aus den Brennstäben entweichen geladene Teilchen in das umgebende Wasser, die wegen ihrer hohen Energie fast Lichtgeschwindigkeit haben. Im Wasser ist die Phasengeschwindigkeit des Lichts eventuell kleiner als die Teilchengeschwindigkeit. Es passiert jetzt das Gleiche, wie wenn ein Schiff auf einer ruhigen Wasserfläche fährt, wenn die Ausbreitungsgeschwindigkeit von Wasserwellen kleiner als die Schiffsgeschwindigkeit ist: Es entsteht eine Bugwelle. Genauso  erzeugen die Teilchen mit fast Lichtgeschwindigkeit elektromagnetische "Bugwellen", weil die Phasengeschwindigkeit von Licht im Wasser kleiner als die Vakuum-Lichtgeschwindigkeit und damit als die Teilchengeschwindigkeit ist. Du hast das auf den Fotos wahrscheinlich als blaues Leuchten aus der Umgebung der Brennstäbe im Abklingbecken gesehen. Diese Lichtstrahlung heißt Tscherenkov-Strahlung. Wenn im Zusammenhang mit der Relativitätstheorie von Lichtgeschwindigkeit c die Rede ist, ist meistens die Vakuum-Lichtgeschwindigkeit c = 2,99792458 · 108 m/s gemeint. Phasengeschwindigkeiten in Materie können durchaus kleiner oder größer als die Vakuum-Lichtgeschwindigkeiten sein, je nach Material und Lichtfrequenz.

2. Die (Vakuum-)Lichtgeschwindigkeit ist unabhängig von der Bewegung des Senders oder des Empfängers oder der Beobachtungsrichtung.

.

Wenn du in einem  mit der Geschwindigkeit u fahrenden Zug einen Ball in Fahrtrichtung wirfst, der im Vergleich zum Zug die Geschwindigkeit v hat, dann würde ein Beobachter am Bahnsteig die Geschwindigkeit u + v für den Ball feststellen. Entsprechend bei einem Wurf in Gegenfahrtrichtung die Geschwindigkeit u - v. Was aber, wenn du statt des Balls einen Lichtstrahl aussendest? Würde etwa ein Beobachter am Zielbahnhof die Geschwindigkeit u + c feststellen, ein Beobachter am Startbahnhof u - c? Im ersten Fall wäre das sogar Überlichtgeschwindigkeit. Nein! Messungen zeigen: Jeder Beobachter, ganz gleich wie er sich im Vergleich zur Lichtquelle bewegt, stellt immer die Geschwindigkeit c = 2, 99792458 · 108 m/s fest (in der Schule kannst du - bei Beachtung der geltenden Ziffern - getrost mit c = 3·108 m/s rechnen). Auch, wenn die Lichtquelle ruht und der Empfänger in Bewegung ist, er wird immer die gleiche Lichtgeschwindigkeit c feststellen. Bei einer bewegten Lichtquelle oder einem bewegten Empfänger ist allerdings der Doppler-Effekt zu beobachten. Die Frequenz des Lichts ist dann bei Annäherung erhöht ("Blauverschiebung": erhöhte Frequenz => verringerte Wellenlänge) und bei Entfernung verringert ("Rotverschiebung": verringerte Frequenz => erhöhte Wellenlänge). Besonders die Rotverschiebung ist ein wichtiges Hilfsmittel, mit dem die Geschwindigkeit von Galaxien als Lichtquellen im Weltall im Vergleich zu uns gemessen wird.

3. Relativ zueinander gleichförmig bewegte Beobachter sehen Vorgänge unterschiedlich ablaufen.

BZS wird im Folgenden als Abkürzung für Bezugssystem verwendet, in dem ein Beobachter ruht.

• Relativität der Gleichzeitigkeit

  Zwei Ereignisse, die für einen Beobachter (in einem BZS) gleichzeitig, aber an verschiedenen Orten stattfinden, finden für einen relativ dazu bewegten Beobachter zu unterschiedlichen Zeiten statt. (Natürlich musste man für diese Aussage unterschiedlich lange Lichtlaufzeiten von den unterschiedlichen Orten korrekt berücksichtigen.)

• Zeitdilation

  Zwischen zwei Ereignissen, die für einen Beobachter am gleichen Ort stattfinden, vergehe eine Zeitspanne Δt. Man nennt sie auch Eigenzeit τ (eigentlich Eigenzeitspanne). Für einen relativ dazu bewegten Beobachter mit der Geschwindigkeit v vergeht zwischen den selben Ereignissen eine längere Zeitspanne Δt', wobei Δt' = Δt //√[ 1 - (v/c)²]  oder Δt' = τ /√[ 1 - (v/c)²].

  Zwei solche Ereignisse am gleichen Ort könnten z.B. Entstehung und Zerfall eines Müons in großer Höhe über der Erdoberfläche (am Ort des Müons) sein. Die Zeitdauer ist so kurz, dass man meinen könnte, sie reiche nicht aus, dass die Müonen durch die Erdatmosphäre hindurch zur Erdoberfläche gelangen. Ein Beobachter am Boden ist jedoch relativ zum Müon mit der Geschwindigkeit -v bewegt. Er stellt zwischen Entstehung und Zerfall eine längere Zeitdauer fest, die ausreicht, dass viele Müonen die Erdatmosphäre durchlaufen können.

• Längenkontraktion

  Ein Beobachter findet zwischen zwei Ereignissen einen Abstand Δx. Die Längenmessung muss er natürlich richtig durchführen, d.h. die beiden Ereignisse müssen gleichzeitig stattfinden. Ein relativ dazu bewegter Beobachter mit der Geschwindigkeit v findet zwischen den selben Ereignissen jedoch einen kürzeren Abstand Δx' = Δx · √[ 1 - (v/c)²].

  Ein solcher Abstand könnte z.B. die Höhe der Erdatmosphäre sein, gleichzeitig gemessen von einem Beobachter auf der Erde. Ein relativ dazu bewegter Beobachter, den du dir im Müon sitzend vorstellen kannst, findet zwischen den beiden Messereignissen jedoch einen kürzeren Abstand, der ausreicht, dass das Müon ihn in seiner Lebenszeit durchlaufen kann.

• Geschwindigkeit - Additionstheorem

  Wenn James Bond aus seinem Spezialfahrzeug, das mit der Geschwindigkeit v fährt, nach vorne auch noch ein Geschoss mit der Geschwindigkeit u relativ zum Spezialfahrzeug abfeuert, wird ein stehendes Hindernis vom Geschoss mit der Geschwindigkeit u' = v + u getroffen. Wenn das für beliebige Geschwindigkeiten so gelten würde, könnte man sich leicht vorstellen, wie Überlichtgeschwindigkeiten entstehen.

  Da dies nicht möglich ist, fügt das Additionstheorem der Geschwindigkeiten eine Korrektur hinzu. Es gilt tatsächlich u' = (v + u)/( 1 + u·v/c²). Wenn z.B. v = c, gilt u' = (c + u) / (1 + u/c) = c. Selbst dieser Extremfall zeigt: Überlichtgeschwindigkeit ist nicht möglich! Wenn ein fast mit Lichtgeschwindigkeit bewegtes Teilchen zerfällt und nach vorn schnelle Teilchen abstrahlt, werden diese nie die Lichtgeschwindigkeit überschreiten können. Werden so Photonen abgestrahlt, wird jeder beliebige Beobachter für sie exakt Lichtgeschwindigkeit feststellen. Werden Teilchen mit Masse auf diese Weise abgestrahlt, wird jeder beliebige Beobachter eine Geschwindigkeit feststellen, die immer noch ein klein wenig geringer als die Lichtgeschwindigkeit ist.

• Impuls - Energie - Masse

  Zwei Beobachter, von denen sich der eine relativ zum anderen mit der Geschwindigkeit v bewegt, stellen unterschiedliche Impulse und Energien (Massen) fest (Begründung später):

  BZS I	BZS II, relativ zu BZS I mit Geschwindigkeit v bewegt
  Impuls p = 0	p = p0 /√[ 1 - (v/c)2] , wobei p0 = m0·v
  Energie E0 = m0 · c2	E = E0 /√[ 1 - (v/c)2 ]
  Masse m0	m = m0 /√[ 1 - (v/c)2 ]

• elektrisches und magnetisches Feld

  Betrachte eine einzelne elektrische Ladung, die im BZS I ruht. Von ihr geht allein ein elektrisches Coulombfeld aus, kein magnetisches Feld. Ein Beobachter in einem BZS II, das relativ zu dem BZS I mit der Geschwindigkeit v bewegt ist, sieht dagegen, dass sich die Ladung mit der Geschwindigkeit -v bewegt, dass sie also einen elektrischen Strom darstellt. Der elektrische Strom erzeugt ein magnetisches Feld, so dass im BZS II sowohl ein elektrisches Feld als auch ein magnetisches Feld vorhanden ist. Und das ist keineswegs ein Effekt, der nur bei sehr hohen Geschwindigkeiten auftritt. Bei kleinen Geschwindigkeiten (v << c) gilt näherungsweise B' = - v/c² x E . Bei kleinen Geschwindigkeiten v kann es allerdings häufig vernachlässigt werden. Umgekehrt, wenn im BZS I ein magnetisches Feld B herrscht (und möglicherweise kein elektrisches Feld), bemerkt ein Beobachter im BZS II zusätzlich zum magnetischen Feld ein elektrisches Feld E'. Bei kleinen Geschwindigkeiten (v << c) gilt näherungsweise E' = - v x B  (Geschwindigkeit -v !). Und das hat selbst bei kleinen Geschwindigkeiten deutliche Konsequenzen.

  BZS I, in dem die Ladung q ruht	Argu- menta- tions- rich- tung	BZS II, relativ zu BZS I mit Geschwindigkeit v bewegt
  ruhende Ladung q	=>	mit -v bewegte Ladung
  Coulombfeld  E' dieser Ladung	=>	zusätzlich noch magnetisches Feld *)
  Magnetfeld B'	=>	zusätzlich noch elektrisches Feld
  elektrische Kraft auf die Ladung  F' = q·E' , wobei E' =   E - v x B in der Näherung für v << c	<=	externes elektrisches und externes magnetisches Feld => Lorentz-Kraft F = q·( E - v x B) (Geschwindigkeit der Ladung -v !)

  Die Lorentz-Kraft ist in diesem Sinne ein relativistischer Effekt, der bereits bei sehr kleinen Geschwindigkeiten (v << c) eine wichtige Rolle spielt. Für den Beobachter in dem BZS, in dem E und B gemessen werden, und für den sich die Ladung bewegt, handelt es sich um die übliche Lorentz-Kraft. Für einen Beobachter, der mit der Ladung mitbewegt ist, für den also die Ladung ruht, kommt (in nichtrelativistischer Näherung) die gleiche Kraft als elektrische Kraft zustande.

  Die RT kommt nicht erst bei Geschwindigkeiten ins Spiel, die vergleichbar mit der Lichtgeschwindigkeiten sind!

• Induktion

  Das macht sich auch bei der Induktion bemerkbar, wenn ein isolierter Leiterstab der Länge ℓ senkrecht zum Magnetfeld mit der Geschwindigkeit v bewegt ist, so dass der Stab die "Feldlinien senkrecht schneidet". Im BZS I bewegt sich der Leiterstab mit der Geschwindigkeit v und wird das Magnetfeld B gemessen. Hier wird näherungsweise für kleine Geschwindigkeiten v argumentiert.

  BZS I	BZS II
  Magnetfeld B, Leiter bewegt sich mit Geschwindigkeit v	Leiter ruht, Magnetfeld B' = B (in erster Näherung)
  An den Elektronen des Leiters greift eine Lorentzkraft F = q v x B, die die Elektronen verschiebt. Es entsteht ein sekundäres elektrisches Feld Es. Schließlich stellt sich ein Kräftegleichgewicht ein: q·v·B = q·Es . Aus dem homogenen Feld Es kann eine "Induktionsspannung" berechnet werden durch U = Es·ℓ = B·v·ℓ	In diesem BZS entsteht (durch Induktion) ein elektrisches Feld E' = v x B. Es verschiebt im Leiterstab Elektronen durch die elektrische Kraft F' = q v x B. Es entsteht ein entgegengesetztes sekundäres elektrisches Feld Es. Schließlich stellt sich ein Kräftegleichgewicht ein:   q · v · B = q · Es . Weiter wie im BZS I.

• Lorentz-Transformation

  Den Übergang von den physikalischen Größen in einem Bezugssystem zu den entsprechenden im relativ dazu gleichförmig bewegten zweiten BZS vermittelt die Lorentz-Transformation, die hier nicht näher beschrieben werden soll.

  Dass dies möglich ist, scheint mir bemerkenswert zu sein. Alle relativ zueinander bewegten Beobachter sehen zwar ein und denselben Vorgang unterschiedlich. Aber jeder kann einfach nachrechnen, wie ihn jeder andere sehen muss. Da ist kein Raum für Willkür, wie sie etwa in dem missverstandenen Slogan "Alles ist relativ" zum Ausdruck kommt.

4. Äquivalenz von Masse und Energie

• Entdeckung der Ruheenergie E₀

Kaufmann und Bucherer und andere hatten zwischen 1901 und 1909 gefunden, dass der Impuls p schneller Elektronen nicht proportional zur Geschwindigkeit v ist. Es gilt nicht mehr, wie in der klassischen Physik p = m·v. Wertet man die Messkurven aus, so findet man p = m·v/√(1 - (v/c)² ). Das Ergebnis lässt sich unterschiedlich deuten.

1. Die historische Deutung besteht darin, dass man sagt "Wir wollen die alte Geschwindigkeits-Impuls-Beziehung weiterhin benutzen, also p = m·v. Die Abweichungen von der Proportionalität stecken wir ganz in den Faktor m, den wir geschwindigkeitsabhängige Masse m nennen. Die klassische Masse nennen wir dann die Ruhemasse m₀." Damit gilt also

Z.B. die Versuche von Kaufmann und Bucherer zeigen ganz klar, dass der Zusammenhang zwischen Impuls und Geschwindigkeit geändert ist. Dass dies durch eine geschwindigkeitsabhängige Masse ausgedrückt wird, ist eine willkürliche Definition, die man früher für sehr nützlich hielt.

Bilde versuchsweise, ohne zu wissen, wozu das gut sein soll, den Ausdruck E₀ = m₀·c² . Er ist von der Dimension einer Energie. Bilde analog E = m·c² = m₀·c² /√[ 1 - (v/c)²] = E₀/√[ 1 - (v/c)²], ebenfalls von der Dimension einer Energie. Wir wollen E relativistische Energie nennen. E₀  heißt dann dazu passend Ruheenergie. Du hast noch keine Vorstellung, ob das überhaupt eine sinnvolle Energie ist. E geht aber in E₀ über, wenn v gegen 0 strebt. E hängt mit dem Betrag des Impulses zusammen: E =  p(v)·c²/v bzw. p(v) = E·v/c². Die letzte Beziehung gilt sogar für v = 0.

Ein Beispiel

Untersuche nun einen vollständig unelastischen Stoß zweier gleicher Massen, die sich im Schwerpunktssystem (BZS I) mit entgegengesetzt gleichen Geschwindigkeiten v aufeinander zu bewegen sollen. Es soll ein zentraler Stoß sein, d.h. er kann wie der Stoß zweier Massenpunkte behandelt werden. Die beiden Massen bilden nach dem Stoße eine vereinigte Masse, die im SPS ruht. Im SPS gelte, wie in jedem beliebigen anderen Inertialsystem, der Energie- und der Impulserhaltungssatz. Beim Stoß entstehende Wärme bzw. zusätzliche innere Energie ist dann mit eingeschlossen.

Wie sieht das in einem BZS II aus, in dem eine der beiden gleichen Massen vor dem Stoß ruht? Es bewegt sich im Vergleich zu BZS I mit der Geschwindigkeit v. Nichtrelativistisch müsste sich dann die andere (relativ zu BZS II) mit 2.v auf die ruhende zu bewegen. Relativistisch kann das nicht stimmen. Denn, wenn z.B. v = 0,6.c, müsste diese Masse dann Überlichtgeschwindigkeit haben. Es gibt stattdessen ein relativistisches "Additionstheorem", das beschreibt, wie sich die Geschwindigkeit des Teilchens v und des Bezugssystems (v , beide relativ zu BZS I) zu einer Geschwindigkeit u (relativ zu BZS II) addieren. Die bewegte Masse hat danach im Vergleich zum BZS II eine Geschwindigkeit u; die vereinigte Masse bewegt sich in BZS II mit der Relativgeschwindigkeit v des BZS im Vergleich zum SPS. In diesem BZS II gilt also

(1) EES (Energie-Erhaltungssatz):      E(u) + E(0) = E'(v)    

In der nichtrelativistischen Mechanik (und bei einem elastischen Stoß) wären das lauter kinetische Energien, wobei E(0) sogar 0 wäre. Was die Energien in der relativistischen Mechanik sein sollen, wissen wir noch nicht. Außerdem handelt es sich hier ja um einen inelastischen Stoß. Wir dürfen auch nicht davon ausgehen, dass sie etwas mit den oben definierten Größen E zu tun haben.

(2) IES (Impuls-Erhaltungssatz):    p(u) + 0 = p'(v) = M'·v     oder m·u = M'·v  

M'.v soll etwas komplizierter geschrieben werden:    M'·v = m·v + α·v     α ist dabei irgendeine Korrekturmasse.

Wir haben dann m·(u - v) = α·v oder m·(u/v - 1) = α.

Nach dem Additionstheorem der Relativität gilt im mit der Geschwindigkeit v bewegten BZS II für die bewegte Masse:    u = 2·v/(1+ß²)   wobei ß = v/c. Eine etwas längere Rechnung liefert damit (u/v - 1) =  √(1 -  ß'²) , wobei  ß' = u/c. Wir haben also erhalten:  m·(u/v - 1) = m √(1 -  ß'²). Das ist aber m₀ . Das ist wiederum α und wir haben α = m₀   identifiziert.

Was haben wir gewonnen? Aus (2) folgt zunächst M' = m + m₀. Multiplizieren wir beide Seiten mit c², heißt das (bei vertauschten Seiten) E(u) + E₀ = M'c² = E'(v) mit unseren formal definierten Energien. Der Vergleich mit dem Energieerhaltungssatz (1) legt nahe: Die zunächst formalen Größen E können nun mit realen Energien E  identifiziert werden. Das wurde erreicht, indem die Relativität zwischen den beiden Bezugssystemen durch das Additionstheorem berücksichtigt wurde.

E₀ durfte also mit Recht als Ruheenergie bezeichnet werden. Es ist eine neue Energieform, die jeder ruhende Körper besitzt, eine bisher unbekannte Art innerer Energie. E ist dann die relativistische Gesamtenergie. Der EES bei relativistischen Stößen darf nicht mehr mit der kinetischen Energie formuliert werden, sondern nur mit dieser relativistischen Energie. E unterscheidet sich von E₀ gerade durch die kinetische Energie. Bei dem Stoß ist zwar mechanische Energie verloren gegangen, aber der Verlust steckt als eine Art innerer Energie in M'.

M' = m + m₀ ist größer als die Ruhemassen beider Stoßpartner. Auch im BZS I gilt für die hier ruhende Masse M'₀ :  M'₀ = m(v) + m(v) > 2·m₀ . In beiden Fällen kommt der Massenüberschuss von innerer Energie.

Wenn du willst, ist das die Entdeckung der Ruheenergie E₀. Einstein ist in seiner RT allerdings etwas anders vorgegangen.

klassische Physik	relativistische Physik
Ekin = m0/2·v2 Bei (elastischen) Stößen wird der EES mit kinetischen Energien formuliert.	E = m·c2  = E0/√[ 1 - (v/c)2] ; E  relativistische (Gesamt-)Energie , E0 = m0c2 Ruheenergie Ekin = E - E0 Bei Stößen muss der EES mit den relativistischen Energien E formuliert werden.
wobei m0 die übliche Masse ist, die jetzt Ruhemasse genannt wird	wobei m = m0/√[ 1 - (v/c)2]  die so genannte relativistische Masse ist

Weil sich in diesem Sinn relativistische Energie und Masse nur durch den Faktor c² unterscheiden, gelten sie als äquivalent.

E = m·c²  ist die wohl bekannteste Formel von Einstein. Ihre enorme Bedeutung erhält die Beziehung bei anderen Vorgängen, bei denen Masse "verlorengeht". Dann muss ein entsprechender Energieanteil abgegeben werden, z.B. in Form von elektromagnetischer Energie. Das ist z.B. bei der Kernspaltung oder der Kernfusion der Fall.

Umgekehrt: Weil sich relativistische Energie und Masse nur durch den Faktor c² unterscheiden, kann der Energieerhaltungssatz auch als Massenerhaltungssatz aufgefasst werden. So wird das in der Schule häufig gemacht.

.

2. Die heute übliche Deutung der Physiker  ist die, dass man nach wie vor von der einen Masse spricht, also von der Ruhemasse.

Elektronen haben in diesem Sinn eine (nicht verschwindende) Masse, Photonen nicht (Ruhemasse = 0). Photonen bewegen sich deshalb mit Lichtgeschwindigkeit.

Physiker  verzichten heute auf eine relativistische Masse und akzeptieren stattdessen den geänderten Zusammenhang zwischen dem Impuls, der Geschwindigkeit und der (Ruhe-)Masse p = m₀·v/√[ 1 - (v/c)²]. In dieser Deutung lässt man die Null oft auch weg. Zur Energie kommt man wie oben durch E =  p(v)·c²/v bzw. p(v) = E·v/c², jeweils mit dem Impulsbetrag.  Eine andere gleichwertige wichtige Energie-Impuls-Beziehung, die für Physiker mehr Aussagekraft hat ist E² = E₀² + p²c². E₀ ist auch hier die Ruheenergie E₀ = m₀c².

Heutige Auffassung der Physiker
Masse = Ruhemasse	m
Impuls	p = m·v /√[ 1 - (v/c)2]
Äquivalenz von Energie und Masse / Ruheenergie	E0 = m·c2
relativistische Energie	E = E0 /√[ 1 - (v/c)2]
kinetische Energie	Ekin = E - E0

Das frühere Konzept von der geschwindigkeitsabhängigen Masse gilt heutzutage unter Physikern als verpönt, weil sich damit die Gleichungen der relativistischen Physik nicht so schreiben lassen, dass sie in allen Bezugssystemen die gleiche Form haben ("sie lassen sich so nicht kovariant schreiben"). Wenn man glaubt, man könne mit einer geschwindigkeitsabhängigen Masse ein Stück weit noch Newtonsche Mechanik betreiben, müsste man sogar zwischen einer longitudinalen (m = m₀ /√[ 1 - (v/c)²]³) und einer transversalen Masse (m = m₀ /√[ 1 - (v/c)²]) unterscheiden, je nachdem in welche Richtung die Kraft im Vergleich zur momentanen Bewegungsrichtung wirkt. Ein solches Konzept mag historisch eine gewisse Bedeutung gehabt haben, es gilt aber heute als völlig überholt.

Wie man an obiger Tabelle und dem folgenden Abschnitt sieht, gewinnt man sogar einige Vereinfachung, wenn man auf die geschwindigkeitsabhängige Masse verzichtet.  Diesen Umweg kann man sich in allen Fällen ersparen.

5. Energie und Geschwindigkeit

Ein Elektron habe die Ruheenergie E₀ = 0,51 MeV und erhalte durch einen Beschleunigungsvorgang aus der Ruhe heraus eine zusätzliche kinetische Energie E_kin = 5 MeV. Es könnte dabei also durch eine Spannung von 5 MV beschleunigt worden sein. Es hat dann die Gesamtenergie E = E₀ + E_kin = 5,51 MeV.

Die Geschwindigkeit erhältst du dann folgendermaßen:

Es gilt:  E = E₀/√(1 - ß² ),   wobei ß = v/c

Die Beziehung muss jetzt nach ß aufgelöst werden. Quadrieren liefert:  

E² = E₀² / (1 - ß²)  bzw.

1 - ß² = E₀²/E²  oder

ß² = 1 - E₀²/E²

Mit Werten für das Zahlenbeispiel also, gerundet

ß² = 1 - (0,51 MeV/5,51 MeV)²  =  0,9914328

ß = 0,9957

bzw. v = 0,9957 · c

Das Elektron hat also fast Lichtgeschwindigkeit erreicht. Für solche Berechnungen brauchst du also weder die Masse des Elektrons (sie steckt in der Ruheenergie E₀), noch Energieumwandlungen in J.

Wenn ein solches - fast schon mit Lichtgeschwindigkeit sich bewegendes - Teilchen noch einmal durch eine zweite Beschleunigung die zusätzliche Energie E₂ = 10 MeV erhält (es wird dann z.B. zusätzlich noch durch eine Spannung von 10 MV beschleunigt), ergibt die Summe von E und E₂ eine neue Gesamtenergie E', aus der wie oben die Geschwindigkeit berechnet werden kann. Sie wird noch ein wenig näher an der Lichtgeschwindigkeit liegen, aber immer noch knapp unter ihr. (Rechne es nach: Es sollte sich ergeben: v = 0,99946 · c ).

Die Werte für die Ruheenergien eines Elektrons (E₀ = 0,511 MeV) und eines Protons (E₀ = 938 MeV) sich zu merken ist lohnend und nicht schwer. Du kannst dann auch leicht entscheiden, wann du relativistisch rechnen musst, bzw. wann eine nichtrelativistische Näherung genügt. Die Faustregel lautet:

(Bei E_kin =  1 % der Ruheenergie ergibt sich v = 0,14 · c . v ist dann 14 % der Lichtgeschwindigkeit. Die beiden Kriterien im Kasten sind also nicht völlig gleichbedeutend.)

Anhang

Umformung des Additionstheorems in einer speziellen Version

Es gilt für den Spezialfall:  u = 2·v/(1+ß²)   wobei ß= v/c

(1) u/v = 2/(1+ß²)  also u/v - 1 =  (1 - ß²)/(1+ß²) ,   andererseits

(2) u/c = ß' = 2ß/(1+ß²)

Bilde 1 -  ß'²  =  1  - 4ß²/(1+ß²)² = ( (1+ß²)² - 4ß² ) /(1+ß²)² = (1 - ß²)² / (1+ß²)² = (u/v - 1)², also

(u/v - 1) =  √(1 -  ß'²) , wobei  ß' = u/c

*) Nicht jedes magnetische Feld entsteht so durch Wechsel in ein Bezugssystem, in dem die Ladung sich bewegt. Bereits ein einzelner ruhender Elektronenspin erzeugt ein Magnetfeld, ebenso ein Verschiebungsstrom (zeitliche Änderung eines elektrischen Felds) und ein Magnetisierungsstrom von vielen wechselwirkenden Spins in einem Festkörpermagneten. In all diesen Fällen entsteht ein Magnetfeld ohne bewegte Ladungen.  (zurück)

( 2012 )

( März 2016: einige Formatierungskorrekturen)