Versuch:

Qualitative Erkenntnisse über das Impulsspektrum eines Quantenteilchens im unendlich hohen Potenzialkasten

Beim linearen Potenzialkasten mit unendlich hohen Wänden ergeben sich stationäre Zustände, also solche mit  be-stimmter Energie, so als könne man ganzzahlige Vielfache einer halben Wellenlänge l  in die Breite des Potenzialkastens 2.d einpassen. Also n.l/2 = 2.d bzw. l = 4.d/n ( n = 1, 2, 3, ... ). In der Schule wird dann oft so argumentiert: Diese Wellenlänge l  hänge mit dem Impuls p nach der deBroglie-Beziehung zusammen: p = h/l, und daraus erhalte man den Impuls und mittels E = p²/2m die Energie E =  h² /(32.d².m) . n² ( n = 1, 2, 3, ... ). Das Ergebnis ist richtig, aber die Behauptung, dass zu einem stationären Energie-Zustand ein be-stimmter Impuls p (oder zwei be-stimmte, durch das Vorzeichen unterschiedene) ist sicher falsch. Deswegen sollte man hier lieber von einem "klassisch denkbaren Impuls" sprechen, den ein klassisches Teilchen mit der gleichen Energie hätte. Allerdings kann man annehmen, dass Abweichungen von dieser Annahme umso geringer ausfallen, je höher das Teilchen angeregt ist (also für n => unendlich).

Mit einem Analogie-Versuch wollen wir uns einen Überblick über das tatsächliche Impulsspektrum verschaffen.

Dazu erzeugen wir uns der Soundkarte und einem geeigneten Programm, wie z.B. GOLDWAVE, akustische Wellenpakete mit unterschiedlichen Längen, zunächst zur gleichen Grundfrequenz f₀.

Mit einem Programm wie GRAM.exe erstellen wir dann ein Sonogramm (Spektrogramm). Dabei gelten die Analogien:

l  entspricht der Wellenlänge der in den Potenzialkasten eingepassten Sinus- oder Cosinusfunktion,

t   entspricht dem Ort x längs des Potenzialkastens

f im Frequenzspektrum entspricht dem Impuls p im Impulsspektrum

Es handelt sich um einen Analogie-Versuch, der nichts mit dem quantenmechanischen Problem zu tun hat. Er benutzt lediglich ein sehr ähnliches Verfahren zur Bestimmung des Frequenzspektrums (so genannte Kurzzeit-Fourier-Transformation), mit dem für ein Quantenteilchen das Impulsspektrum berechnet werden könnte (Fourier-Transformation). Zu den dargestellten Frequenzanteilen muss man sich beim Quantenteilchen noch negative Impulsanteile hinzudenken.

Die Programme GOLDWAVE und GRAM können Sie, zumindest in Erprobungsversionen, kostenlos aus dem Internet herunterladen.

Versuch 1:

Frequenzspektrum zu sinusförmigen Wellenpaketen endlicher Länge mit jeweils der gleichen Grundfrequenz f₀

Mit einem Sound-Programm wie GOLDWAVE wird eine Sinusschwingung erzeugt (TOOLS/EXPRESSION EVALUATOR), z.B. mit f₀ = 320 Hz. Aus ihr werden unterschiedlich lange Wellenzüge ausgeschnitten (1/2, 1, 2, 5, 10, 20, ... ) und in eine gemeinsame Datei kopiert (z.B. x1.wav).

Diese Datei wird in GRAM eingelesen und mit GRAM analysiert.

(Die Parametereinstellungen beim Programm GRAM erfahren Sie hier.)

Es ergibt sich ein Bild ähnlich wie dieses:

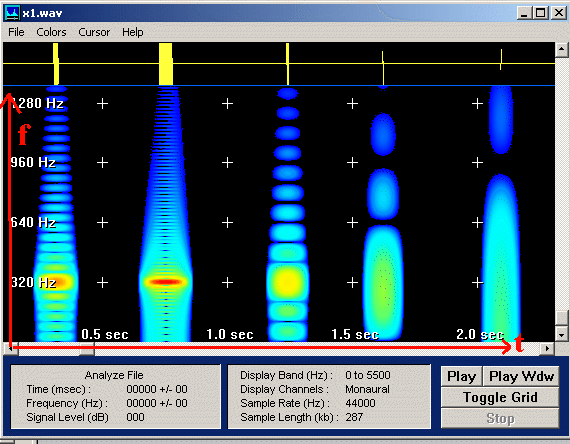In der ersten Zeile des Spektrogramms von GRAM (oberhalb der blauen Linie) kann man den Zeitverlauf der einzelnen Wellenpakete erahnen. In allen Fällen besteht das Frequenzspektrum aus vielen Anteilen, keineswegs nur aus dem ursprünglich erzeugten mit 320 Hz. Bei kurzen Wellenzügen ist die Verteilung  der Frequenzen breit; das Maximum bei  der Grundfrequenz ist nicht sehr ausgeprägt. Je länger der Wellenzug, desto mehr konzentriert sich die Verteilung um die Grundfrequenz (immer mehr durch rot markiert). Bei einem sehr langen Wellenzug wäre die Frequenzverteilung sehr schmal, eng konzentriert um die Grundfrequenz.

Ergebnis:

E

Je kürzer der Wellenzug der festen Grundfrequenz, desto breiter und unstrukturierter ist die Frequenzverteilung. Je länger der Wellenzug, desto  mehr bildet sich ein Maximum der Frequenzverteilung bei der Grundfrequenz heraus. Übertragen auf das Quantenteilchen im Potenzialkasten heißt das: Je tiefer die Energie des stationären Zustands ist ("je weniger halbe Wellenlängen in den Potenzialkasten eingepasst werden"), desto breiter und unstrukturierter ist die Impulsverteilung. Man muss sich die Verteilung symmetrisch vorstellen mit einem Maximum bei p = +/- h/l . Je größer die Energie des stationären Zustands ist ("je mehr halbe Wellenlängen in den Potenzialkasten eingepasst werden"), desto schärfer bilden sich zwei Maxima der Impulsverteilung bei p = +/- h/l  heraus. Der Grenzfall würde einem klassischen Teilchen entsprechen, das sich mit diesen beiden Impulsen im Potenzialkasten hin und her bewegt.

Versuch 2:

Wir erzeugen uns der Soundkarte und einem geeigneten Programm, wie z.B. GOLDWAVE, akustische Wellenpakete mit der Wellenlängen l = l_o/n (n = 1, 2, 3, ... ), also mit den Frequenzen f = f₀.n. Der Einpassung in den Potenzialkasten entspricht, dass wir mit den Copy und Paste-Funktionen des Programms gleich lange Stücke ausschneiden, die "der konstanten Breite des Potenzialkastens entsprechen".

Der weitere Gang des Versuchs geht wie Versuch 1.

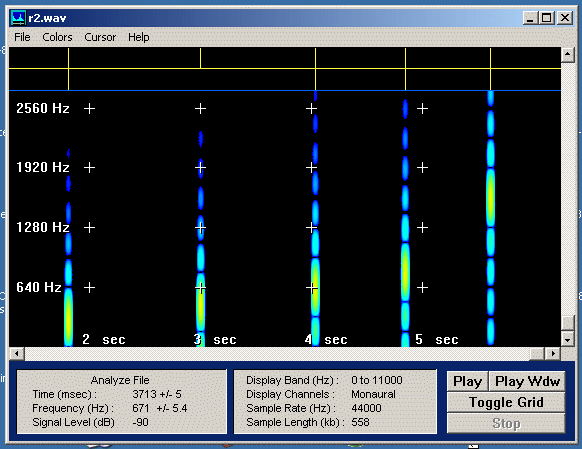Jeweils gleiche Länge des Wellenzugs. Einpassung von zunehmender Zahl von Wellenlängen: Mit zunehmender Grundfrequenz f  nimmt auch das Maximum der Frequenzverteilung zu. Es tritt dabei immer stärker hervor. (Bei sehr viel längeren Wellenzügen sollte man dem so erzeugten Spektrogramm allerdings nicht mehr trauen: Dann macht es sich bemerkbar, dass eine Kurzzeit-Fouriertransformation verwendet wird und keine normale Fouriertransformation.)