Der FKG-Roboter FORPHYS- Mess- Interfaces Forschendes Lernen im Physik-UR Würzburger Quantenphysik- Konzept Grundfakten der Quantenphysik Materialien Physik-UR Physikalische Analysen Experiment des Monats Physik für Schüler Impressum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2012

Ziel:

Eigenschwingungen stellen m.E. die größte Annäherung der klassischen Physik an quantenphysikalische Eigenzustände, z.B. Energiezustände mit diskreten Energien, dar. Diesem Anspruch können m.E. keine klassischen Systeme genügen, bei denen lediglich mehrere Minima der potenziellen Energie vorkommen, wie etwa Verschlüsse von Milchtüten oder Sprungbretter. Es lohnt sich deshalb, dieses Thema im Unterricht genauer zu behandeln.

Das ist nur bei bestimmten Frequenzen möglich, den so genannten Eigenfrequenzen. Das lässt sich für ein System von einzelnen schwingenden Massen auch visuell veranschaulichen.  Dazu könnten gekoppelte Pendel oder eine Simulation mit dem Programm WELLEN dienen. Multipliziert man dieEigenfrequenzen mit dem Planckschen Wirkungsquantum h kommt man formal zu diskreten Energien, wie z.B. für ein Elektron im linearen Potenzialkasten oder im Atom.

Eigenschwingungen sind dennoch etwas völlig anderes als Eigenzustände. Erregt man das klassische System mit einer der Eigenfrequenzen, schwingt es nach dem Einschwingvorgang mit besonders großer Amplitude. Die Eigenschwingung wird so erkennbar. Ein klassisches System schwingt aber mit jeder beliebigen (Erreger-)Frequenz, wenn auch mit u.U. sehr kleiner Amplitude. Die Bedingung "alle Teile schwingen mit gleicher Frequenz" wird aber nur für die Eigenschwingungen eingehalten. Ein Messwert für die Energie eines (abgeschlossenen) Quantensystems kann dagegen nur exakt einer der erlaubten Energie-Eigenwerte sein. Befindet sich das System in einem Eigenzustand, misst man immer die gleiche Energie. Bei Überlagerungszuständen erhält man streuende Messwerte.

Erhält man also in einem quantenphysikalischen Zustand immer die gleichen Messwerte für die Energie, besteht also noch eine weitergehende Analogie zwischen Eigenschwingungen und Eigenzuständen.

Durch diese Versuche sollen Sie

erkennen, dass eine Gassäule viele Eigenfrequenzen besitzt

eine Gesetzmäßigkeit für die Eigenfrequenzen herausfinden

[ die Gesetzmäßigkeit modellmäßig deuten durch das Einpassen von halben Wellenlängen (die Möglichkeit wird hier erwähnt, führt aber m.E. für das Thema Quantenphysik auf Abwege.]

ein "Frequenzniveauschema" als Vorbereitung für ein "Energieniveauschema" kennen lernen und zeichnen

die Bedingung "stets gleicher Messwert" (hier für die Frequenz aller Teile) zum Verständnis von Energie-Eigenwerten vorbereiten

Eine ebenfalls naheliegende Interpretation durch stehende Wellen  ist in dieser Stunde nicht angestrebt, weil für das quantenphysikalische Ziel stehende Wellen im Sinne von hin- und herlaufende Wellen nicht hilfreich erscheinen (Vgl. Wahrscheinlichkeitsinterpretation der Wellenfunktion im Konfigurationsraum und nicht im Anschauungsraum)

Hier werden Eigenschwingungen einer Gassäule in einem beidseitig offenen Rohr der Länge ℓ untersucht. Sie werden durch einen Lautsprecher angeregt, der von einem Funktionsgenerator oder Mikroprozessor versorgt wird. Dazu ist z.B. das FORPHYS-Messinterface geeignet. Das Messinterface ersetzt einen konventionellen Funktionsgenerator mit einstellbarer Frequenz. Als Sensor dient das Ohr. Der Versuch ist also auch mit konventionellen  Mitteln durchführbar. Vorteil des preiswerten Messinterfaces mag sein, dass der Versuch mehrfach von Schülergruppen durchgeführt werden kann, dass die Erregerfrequenz jeweils exakt bekannt ist.

Das positive Rechteckssignal des Mikroprozessors entspricht einem symmetrischen Rechteckssignal gleicher Frequenz mit einem überlagerten Gleichspannungsanteil. Deshalb ist es sinnvoll, den Gleichstromanteil mittels eines Kondensators (C > 1 µF) abzublocken. Es ist belanglos, dass dann der Lautsprecher natürlich nicht mehr mit einem Rechteckssignal betrieben wird. Wenn der Lautsprecher dicht vor die eine Rohröffnung gesetzt wird, entstehen Eigenschwingungen einer halboffenen Röhre.

[ Der Lehrer weiß: Dann gilt: f = f₀.(1 + 2· k)   k ε N₀    wobei für die Grundfrequenz f₀ gilt:  f₀=  c/4· ℓ  

Weil:     λ/4 + k · λ/2 = ℓ , also   λ = ℓ / (1/4 + k/2)   λ = 4ℓ  /(1 + 2· k)   ;  λ₁ = 4ℓ , λ₂= 4ℓ /3 ,  λ₃ = 4ℓ /5   ]

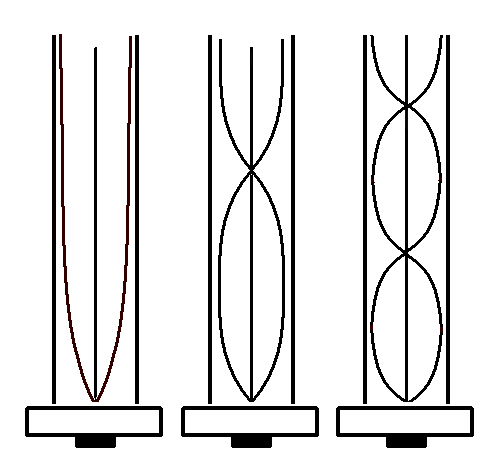Abb. 1: Am offenen Ende bilden sich Bewegungsbäuche (und Druckknoten) aus, Voraussetzung für gute Hörbarkeit. (Im Bild wird die Schallschnelle dargestellt.) Am Lautsprecher  (unten) ist die Situation unschärfer, weil einerseits nur Anregung durch eine sich bewegende Membran erfolgt, andererseits die Membran doch eher wie ein Reflektor wirkt. In guter Näherung entsteht dort ein Druckbauch, wenn der Lautsprecher unmittelbar vor der Rohröffnung steht.

Für das Versuchsziel  sind keine Deutung durch stehende Wellen und keine Hinweise auf longitudinale oder transversale Wellen notwendig oder erwünscht.