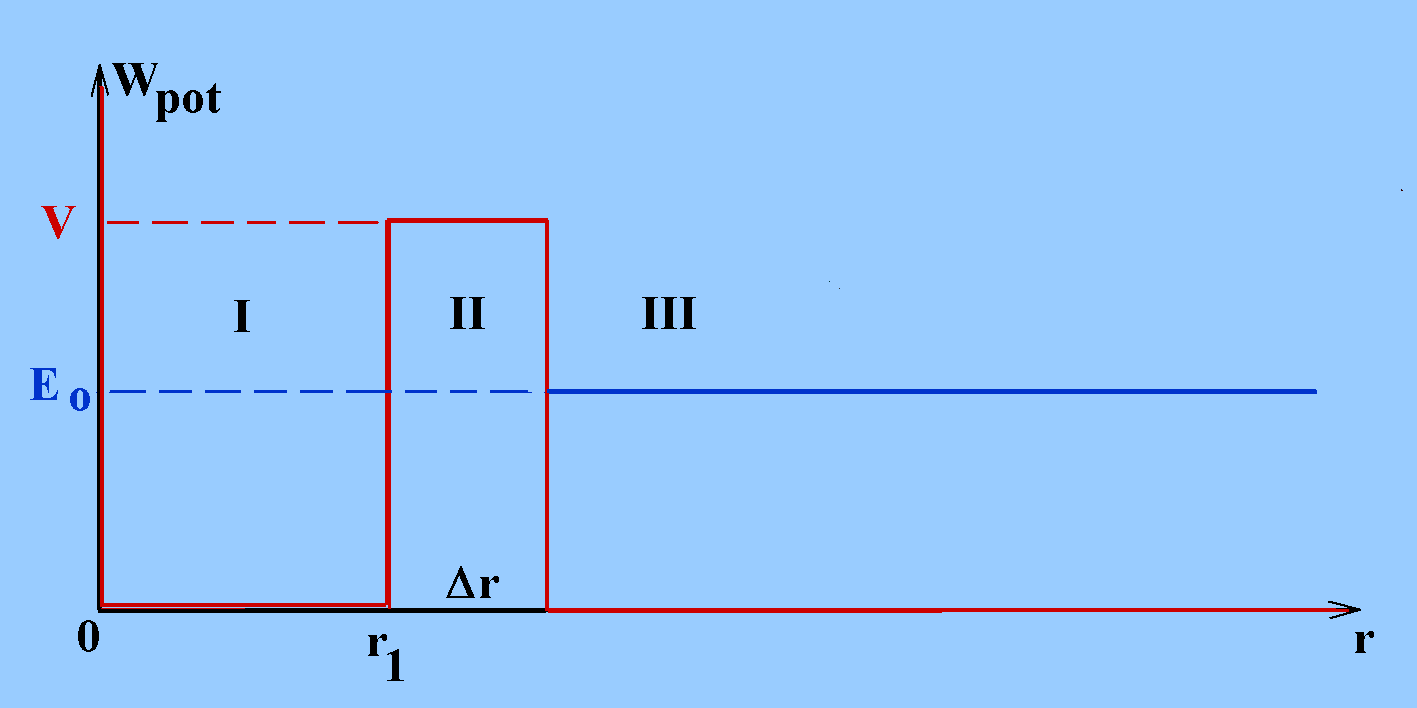
Bereich I stellt einen Potenzialtopf dar, Bereich II einen Potenzialwall.
Außerhalb - weit weg vom Kern - habe das Teilchen die (kinetische) Energie Eo.
|
G83 Der Tunnel-Effekt und der α-Zerfall |
Potenzielle und kinetische Energie Heisenbergsche Un-be-stimmtheitsrelation |
Nach dem Tunnel-Effekt kann ein (Quanten-)Teilchen auch in Raumbereichen nachgewiesen werden, in denen es sich nach klassischer Vorstellung gar nicht aufhalten dürfte. Insbesondere würde eine Potenzialbarriere, ein Potenzialwall bzw. eine Potenzialschwelle in der klassischen Physik den Durchtritt verhindern, wenn die Energie des Teilchens die potenzielle Energie in der Barriere nicht überwinden könnte (siehe auch Potenzialgebirge).
Betrachten Sie ein sehr primitives Modell eines Atomkerns, der α-Teilchen emittiert. Solche Teilchen seien im Kern "locker gebunden". Würden Sie austreten, müssten sie eine Potenzialbarriere der Höhe V überwinden. Klassisch kann man sich vorstellen, dass es α-Teilchen im Kern gibt, deren kinetische Energie im Bereich I zu gering ist, um im Bereich II einen Teil davon in potenzielle Energie umzuwandeln. Oder anders: Die Differenz zwischen potenzieller Energie und Gesamtenergie ist die kinetische Energie. Sie müsste nach dem Energieerhaltungssatz im Bereich II negativ sein, was nicht möglich ist. Solche Teilchen könnten nach klassischer Vorstellung den Innenbereich des Kerns (I) also nicht verlassen. Andere Teilchen mit höherer kinetischer Energie (> V) wären gar nicht gebunden. Sie würden sich von einem einzelnen Kern schnell irgendwo hin entfernen. Teilchen mit negativer (Gesamt-)Energie wären echt gebunden und könnten den Kern ohne äußere Einwirkung überhaupt nicht verlassen. Sie werden im Modell nicht beachtet.
 |
In der Zeichnung sei der Radialanteil der Potenzialfunktion Wpot
eines kugelsymmetrischen Teilchens dargestellt. (Man kann
sich aber auch vorstellen, dass hier ein eindimensionales Problem
vorliegt.) Durch ein "unendlich hohes" Potenzial bei r = 0 wird
verhindert, dass negative r-Werte erreicht werden (im
kugelsymmetrischen Modell ist das selbstverständlich).
Bereich I stellt einen Potenzialtopf dar, Bereich II einen Potenzialwall. Außerhalb - weit weg vom Kern - habe das Teilchen die (kinetische) Energie Eo. |
Im quantenmechanischen Fall müssen wir einige Warnschilder beachten:
Das allein stellt schon die klassische Argumentation in Frage.
Der kritische Bereich ist der Bereich II. Wir wollen mit Hilfe der HUR
hier halbklassisch abschätzen, in welchem Bereich Messungen der
kinetischen Energiezu erwarten sind, nachdem wir ein Teilchen in der
Potenzialbarriere lokalisiert haben. Dann ist der Ort offenbar nur noch
un-be-stimmt innerhalb eines Bereichs Δr. Nach der HUR
in der üblichen Form Δr·Δpr >= ħ
ergibt sich daraus eine (radiale) Impuls-un-be-stimmtheit Δpr
>= ħ
/ Δr. ħ
ist dabei wieder das Plancksche Wirkungsquant h dividiert durch 2p.
Sie führt zu einer Un-be-stimmtheit der kinetischen Energie im Bereich II:
ΔEkin >= p2/2m = ħ2
/ ( Δr2 2m ) *). Das heißt: Wenn
ein Teilchen im Bereich II festgestellt wurde, dann ist erstens seine
potenzielle Energie (als Funktion des Ortes) einigermaßen be-stimmt,
nehmen wir an, sie sei ungefähr V. Zweitens ist seine kinetische Energie
un-be-stimmt innerhalb der Unschärfe ΔEkin. Es wird durchaus
Messwerte geben, die V sogar überschreiten. Wer wollte dann noch
verbieten, dass das Teilchen im Bereich II nachgewiesen wird? In diesem
Fall verbieten nicht einmal klassische Argumente, dass es dann auch im
Bereich III nachgewiesen wird.
[Auch im Bereich I ist die kinetische Energie un-be-stimmt. Nach einer Ortsmessung (es genügt dafür die sichere Kenntnis: "Kern nicht zerfallen") mit der Orts-un-bestimmtheit Δr = r1 erhalten wir für die Energie-un-be-stimmtheit ΔEkin >= ħ2 / ( r12 2m ). Auch sie kann die Höhe der Potenzialfunktion im Bereich II überschreiten und damit das klassische Argument hinfällig machen.]
Die Erscheinung, dass α-Teilchen, deren Energie nach klassischer Vorstellung ein Durchdringen der Potenzialbarriere verhindern würde, nach klassischer Sprechweise wie durch einen Tunnel die Potenzialbarriere durchdringt und so den Kern verlässt, heißt Tunneleffekt. Sie ist der Grund für den α-Zerfall bestimmter Atomkerne. Sie wurde hier durch die HUR (Heisenberg'sche Unbestimmtheitsrelation) erklärt.
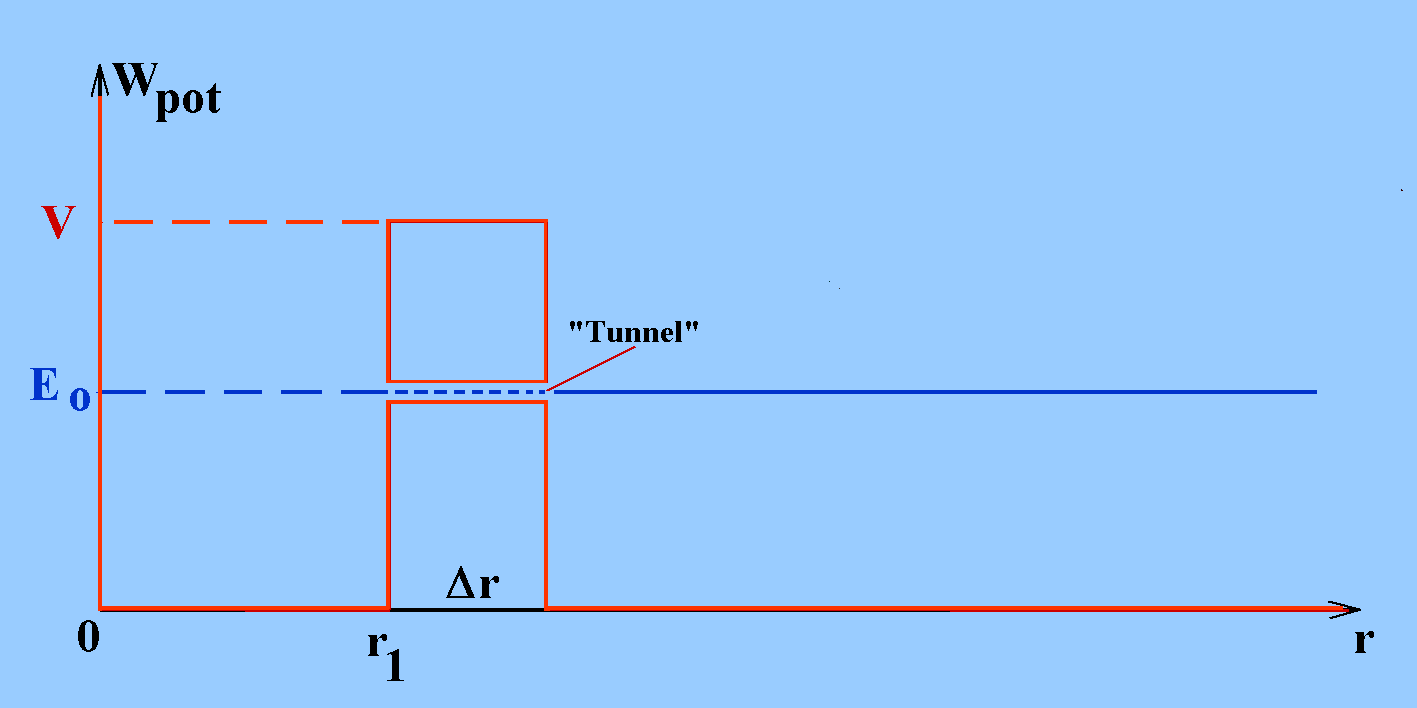 |
Klassisches Bild vom Tunneln eines Teilchens durch eine
Potenzialbarriere.
Quantenphysikalisch sind in der Abbildung sowohl die Annahme einer Bahn des Teilchens wie von einer be-stimmten kinetischen und potenziellen Energie innerhalb der Potenzialbereiche I und II nicht haltbar. Die Energie-un-be-stimmtheit ΔEkin >= ħ2 / ( Δr2 2m ) im Vergleich zur Höhe der Potenzialbarriere V zeigt, dass das Tunneln um so wahrscheinlicher wird, je schmaler der Bereich der Potenzialbarriere Δr und je geringer ihre Höhe V ist. |
Eine Warnung: Die gezeichnete "Potenzialfunktion" Wpot ist nach der Quantenphysik i.A. nicht die potenzielle Energie eines Teilchens. Voraussetzung dafür, dass man für jeden Ort eine potenzielle Energie angeben könnte, wäre, dass gleichzeitig Ort und potenzielle Energie (durch eine Messung) exakt be-stimmt wären. Dann wäre die kinetische Energie beliebig un-be-stimmt. Deswegen wird die obige Abschätzung halbklassisch genannt.
*) Wegen E = p2/2m ergibt sich durch Ableiten ΔE = p/m Δp = √2E/m Δp . Das wäre eine für manche Zwecke günstigere Abschätzung als die verwendete.