Frage
Antwort
Warum können Geschwindigkeiten positiv und negativ sein, während Tempo-Angaben nie negativ sind?
Im Unterschied dazu beschreibt "Tempo" den Betrag der Geschwindigkeit. Eine Richtungsangabe fehlt. Ein Tachometer im PKW zeigt Tempo an. Während umgangssprachlich überwiegend Tempo verwendet wird, in der Physik eigentlich nur Geschwindigkeit, wird in der Didaktik genau zwischen Tempo und Geschwindigkeit unterschieden. Ähnlich werden in angelsächsischen Ländern zwei unverwechselbare Begriffe - speed (Tempo) und velocity (Geschwindigkeit) - verwendet.
In manchen Schulbüchern wird die Gleichung
Eine solche Definition bewährt sich erst dann, wenn man mit ihr etwas anfangen kann. Und genau das entdeckte Newton! Ein Beispiel soll das erläutern. Man lasse einen Körper der Masse m fallen, messe die Fallbeschleunigung und definiere damit die Gewichtskraft F = m.g, die auf den Körper wirkt. Wenn man jetzt beliebige lineare Bewegungen von Körpern mit beliebiger Masse M unter dem Einfluss dieser Gewichtskraft F untersucht, erhält man immer eine Beschleunigung a, die sich aus a = F/M berechnet. Das ist nun wirklich eine gesetzmäßige Folgerung aus dem 2. Newton-Gesetz. Damit gelang es Newton - nach dreidimensionaler Verallgemeinerung - z.B. den Bau unseres Planetensystems aufzuklären.
Wenn du in einer ersten Einführung in die Physik von der Definitionsgleichung erfahren hast, wirst du später die gesetzmäßigen Inhalte des 2. Newton-Gesetzes erfahren, zu dem die gleiche "Formel" gehört, aber viel mehr Bedeutung.
Dagegen ist die Masse wirklich Eigenschaft eines Körpers. Die Masse eines Körpers ist ein Maß für seine Trägheit, aber auch seine "Gravitationsladung". Wegen der letzteren Eigenschaft hängt die Anziehungskraft von zwei Sternen von ihren beiden Massen und ihrem Abstand ab. Genauso hängt die Gewichtskraft, die auf einen Körper mit der Masse m wirkt, von dieser Masse, aber auch der Masse der Erde und dem Abstand der Zentren beider Körper ab.
Schulbücher, in denen von "der Gewichtskraft eines Körpers" die Rede ist, sollten korrigiert werden zu "Gewichtskraft, die auf einen Körper wirkt".
Warum kann ein Akku oder eine Batterie i.A. keine potentielle Energie produzieren?
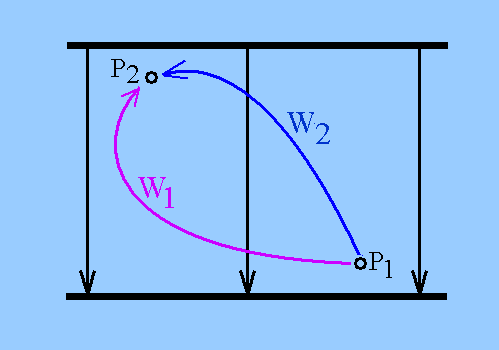 |
Im geladenen Kondensator sind die
Verschiebungsarbeiten bei beliebigen Wegen zwischen
Ausgangspunkt und Endpunkt gleich: Es lässt sich
eine potenzielle Energie der verschobenen Ladung
angeben, die (bei festem Bezugspunkt P1)
allein eine Funktion des Orts P2 ist.
Die Wegunabhängigkeit der Verschiebungsarbeit begründet hier die Existenz eines Potenzials. Ein typisches Anwendungsbeispiel ist die Umwandlung von potenzieller Energie einer Ladung in kinetische Energie bei der Bewegung in dem vorgegebenen Potenzialfeld des Kondensators.
|
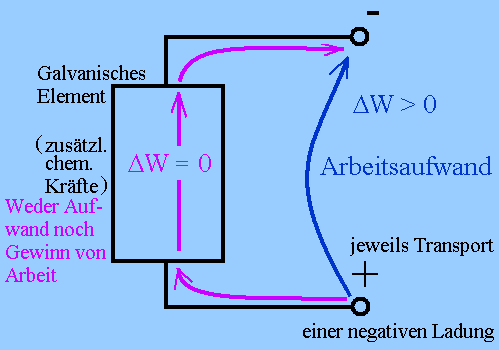 |
Bei Verschiebung einer negativen Ladung von P1
nach P2 im Außenraum eines galvanischen
Elements (oder einer anderen Stromquelle) ist
Arbeitsaufwand nötig, nicht dagegen für eine
Verschiebung zwischen den gleichen Punkten, wenn die
Verschiebung durch das galvanische Element hindurch
erfolgt. In diesem Fall heben sich die chemischen Kräfte
und die elektrische Abstoßungskraft ungefähr auf.
Trotz gleichen Anfangs- und Endpunkts der Verschiebung ist die Verschiebungsarbeit unterschiedlich. Es lässt sich - streng genommen - keine potenzielle Energie als Funktion des Orts allein definieren. Bei Stromfluss wirken i.A. zwei nichtkonservative Kräfte: die chemischen "Kräfte" in der galvanischen Zelle und die dissipativen Kräfte in den stromdurchflossenen Widerständen. |
Bei einem geladenen Kondensator existiert sicher eine potenzielle Energie. Bei seiner Entladung über einen Widerstand wirken aber auch dissipative Kräfte. Dem widerspricht das obige Argument m.E. nicht, da man die Verschiebung durch den Widerstand (einer der beiden zu vergleichenden Wege) prinzipiell beliebig langsam durchführen könnte, so dass im Widerstand keine Energieverluste auftreten. Auf jeden Fall würde hier bei der Kondensator-Entladung - auf jeden Fall vorher vorhandene - potenzielle Energie (Feldenergie) in Wärme umgewandelt werden.
Es ist keine Aussage über die Temperatur, denn auch andere Systeme als ein ideales Gas können eine Temperatur haben, sogar Systeme, die überhaupt keine kinetische Energie haben. Ein Spinsystem, wie etwa in einem Ferromagneten, oder das Photonengas in einem evakuierten Hohlraumstrahler oder die Hintergrundstrahlung aus einer bestimmten Phase des Urknalls sind Beispiele dafür.
In diesem Sinn kann man auf die Frage, ob ein Vakuum eine Temperatur hat, zwei verschiedene Antworten geben:
- Ein reales Vakuum enthält unvermeidbar Strahlung. Diese hat eine Temperatur, wenn die Strahlung im thermischen Gleichgewicht ist.
- Ein absolutes Vakuum (auch ohne Strahlung) gibt es nicht. Also ist die Frage hinfällig. Und: Temperatur ist ja immer die Temperatur von "etwas".
Hängt nicht auch die potenzielle Energie der Atome des Gases von der Temperatur T ab?
Bei anderen Systemen (z.B. realen Gasen, Festkörpern, Flüssigkeiten) ist auch die mittlere potenzielle Energie von der Temperatur abhängig, in einigen Fällen sogar in der gleichen Weise wie die mittlere kinetische Energie.
Und andere Systeme, wie das Photonengas der Hohlraumstrahlung, haben zwar im thermischen Gleichgewicht eine innere Energie und Temperatur, aber weder kinetische noch potenzielle Energie. Beim Stefan-Boltzmann-Gesetz wird das genutzt.
Warum kann eine Spannung nicht die Ursache für einen Strom sein?
Es gibt einige Beispiel, wo ein Strom ohne eine Spannung fließt. Bei der Supraleitung kann ein Ringstrom in einem geschlossenen Stromkreis ohne eine Stromquelle jahrelang fließen, weil kein Widerstand im Stromkreis vorhanden ist. In einem Wechselstromkreis oder in elektromagnetischen Schwingkreisen gibt es Zeitpunkte, bei denen die Spannung 0 ist, wobei aber gerade maximaler Strom fließt. Und es gibt einige andere Beispiele in der Schulphysik, wo ein Strom sogar gegen eine Gegenspannung fließen kann, beim Photoeffekt etwa.
Beim Spannungsabfall an einem stromdurchflossenen Widerstand ist die Spannung sogar die Folge eines Stroms. Unterbricht man den Strom, dann werden alle Spannungsabfälle sofort zu 0.
Nein, die mit einer Spannung zusammenhängende Energiezufuhr ist nicht dazu nötig den Strom fließen zu lassen, sondern um Energieverluste in Widerständen zu ersetzen.
Zum Ersatz der Energieverluste führt man Energie (Strom-Arbeit) zu, für deren Größe die Spannung ein Maß ist.
Ist ein Strom die Folge einer Spannung oder die Spannung eine Folge des Stroms?
Allerdings würde die Stromstärke in den meisten Fällen wegen der "Stromreibung" u.U. schnell abnehmen. In vielen Fällen werden also Energieverluste durch eine äußere Spannung ersetzt, damit ein stationärer Strom fließt. Das ist die eigentliche Rolle einer Stromquelle in einem normalen elektrischen Stromkreis.
Wenn ein Strom durch Widerstände fließt, dann erzeugt er zwischen deren Enden einen Spannungsabfall, der von der Stromstärke abhängt. Dass hier die Spannung wirklich eine Folge des Stroms ist, erkennt man daran, dass dieser Spannungsabfall verschwindet, wenn man irgendwo im Kreis den Strom unterbricht.
Ist ein elektrischer Strom immer mit einer Trennung von Ladungen verbunden?
Von einer Ladungstrennung beim Stromtransport kann man hier also nicht sprechen. Oder auch anders: In Metallen sind die frei beweglichen Leitungselektronen und die Atomrümpfe nach dem Modell des freien Elektronengases (oder der Fermi-Flüssigkeit) immer "getrennt", ob nun eine Spannung anliegt oder nicht. Auch in Elektrolyten (wie in einer galvanischen Zelle) findet eine Dissoziation in positive und negative Ionen bereits unabhängig von elektrischen Vorgängen statt. Durch elektrische oder chemische "Kräfte" können diese zu entgegengesetzten Polen in Bewegung gesetzt und so räumlich getrennt werden.
In einem homogenen geschlossenen Leiterring aus einem gut leitfähigen Material kann durch ein sich änderndes Magnetfeld ein Induktionsstrom induziert werden. Die Induktion ist hier mit keinerlei Ladungstrennung verbunden. Es gibt nirgendwo einen Pluspol oder einen Minuspol, und doch fließt ein Induktionsstrom!
Entsteht am Hall-Generator oder MHD-Generator potenzielle Energie?
An einem Punkt P1 habe eine Ladung eindeutige Energie, das Magnetfeld sei auf den Bereich des Hall-Plättchens beschränkt, das es senkrecht durchsetze. Bringt man die Ladung zu einem Punkt P2 auf der gegenüberliegenden Seite des Plättchens, die sich durch die Lorentzkraft negativ aufgeladen hat, dann ist die dazu nötige Arbeit abhängig davon, ob man die Ladung außerhalb des Hall-Plättchens/Magnetfelds oder durch das Plättchen zu P2 verschob.
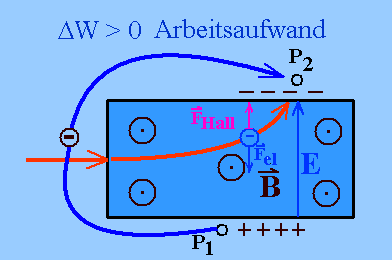 |
Bei einer Verschiebung im Plättchen bzw.
Magnetfeld ist im stationären Fall keine Arbeit
aufzuwenden (ΔW = 0), weil sich die Lorentzkraft FHall
und die resultierende elektrische Kraft Fel
gerade aufheben, wohl aber im Außenraum (auf dem
gezeichneten Weg ΔW > 0).
Trotz gleichen Anfangs- und Endpunkts der Verschiebung ist die Verschiebungsarbeit in beiden Fällen unterschiedlich. Es lässt sich - streng genommen - keine potenzielle Energie als Funktion des Orts allein definieren. |
Früher - als man die Dynamik lieber in Form der damals vertrauteren Statik formulierte - schrieb man das 2. Newton-Gesetz F = m·a auch in einem Inertial-System gern in der Form F - m·a = 0 und nannte - m·a "d'Alembertsche Trägheitskraft". Das ist heute nicht mehr üblich.
Gibt es eine "relativistisch bewegte" Masse, bzw. hängt die Masse von der Geschwindigkeit ab?
Früher dagegen definierte man eine bewegte Masse m = m0 /√[1- (v/c)2] und behielt dann p = m·v bei. Das ist heute in der Schule auch meistens noch so üblich. Leider !
a) durch "Trennarbeit"?
b) durch einen Unterschied in der potenziellen Energie zweier hypothetischer Ladungen an den beiden Punkten?
c) durch die Arbeit pro Ladung, die verrichtet wird, wenn man eine hypothetische Ladung von einem Punkt zum anderen verschiebt?
b) Ja, bringt man eine Ladung Q an einen der beiden Punkte und verschiebt diese dann zum anderen Punkt, so muss Arbeit aufgewendet (oder entzogen werden) - wenn nicht auch kinetische Energien beteiligt sein sollen, beliebig langsam. Bei Arbeitsaufwand ist die Arbeit dann als erhöhte potenzielle Energie in der verschobenen Ladung enthalten. In diesem Fall existiert ja auch ein Potenzial.
c) Ja, ganz entsprechend. Oder, wenn die Ladung ursprünglich eine höhere Energie hat, dann gibt sie Arbeit nach außen ab, wenn sie (beliebig langsam) zu dem Punkt mit der niederen Energie wandert. Durch langsame Bewegungen sorgt man immer dafür, dass nirgendwo kinetische Energien beteiligt sind.
Dennoch kann der fließende Induktionsstrom Stromarbeit verrichten, d.h. nach außen abgeben. Was hat das mit Spannung zu tun?
Bei Stromfluss durch Widerstände längs der Schleife entstehen Spannungsabfälle zwischen 2 Punkten A und B als Folge des Stroms. Diese entsprechen der Arbeit pro Ladungseinheit bei Verschiebung der Ladung (Stromtransport) zwischen den beiden Punkten.
Die durch DIN 1324 festgelegte Definition einer Spannung über die Verschiebungsarbeit pro Ladungseinheit funktioniert in allen Fällen, unabhängig davon, ob ein Potenzialfeld vorliegt oder nicht.
Warum bleibt die Temperatur während des Siedens oder Schmelzens konstant?
Schauen wir uns das beim Sieden an. Durch Energiezufuhr wird Arbeit gegen die Bindungskräfte der Moleküle verrichtet. Die potenzielle und die kinetische Energie einiger Moleküle in der Flüssigkeit steigen schließlich soweit, dass die Bindungskräfte überwunden werden. Die schnellsten Moleküle mit der höchsten Energie verlassen damit die Flüssigkeit ohne zur mittleren Energie der verbleibenden Flüssigkeitsmoleküle beizutragen.
Zur Dampfphase dagegen treten die "abgedampften" Moleküle hinzu, aber immer mit derselben Energie, am unteren Ende der Energieskala. Auch sie können nichts beitragen zur mittleren Energie der Moleküle in der Dampfphase. In beiden Phasen bleiben also die Temperaturen konstant und untereinander gleich, bis alle Moleküle aus der Flüssigkeit in die Dampfphase übergetreten sind.
Durch die Energiezufuhr wird auf jeden Fall die innere Energie beider Phasen zusammen gesteigert, die mittlere Energie (potenzielle wie kinetische) in jeder der beiden Phasen wird nicht geändert, weil Moleküle zwar mehr Energie aufnehmen können, dann aber die Flüssigkeitsphase verlassen, und weil zur Dampfphase nur solche Moleküle hinzutreten, die quasi die Energie der Ablösung von der Flüssigkeitsphase besitzen.