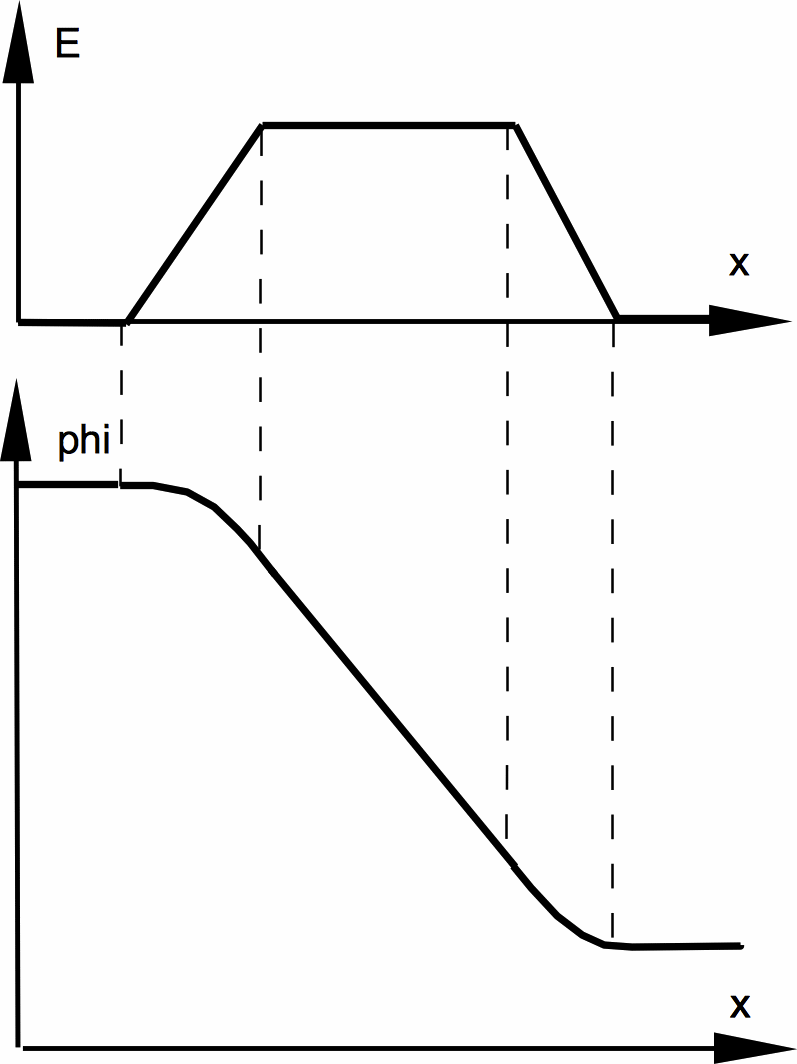
Dem Potenzialverlauf entspricht auch die potenzielle Energie eines Leitungs-Elektrons (L-Elektrons), jedenfalls außerhalb der Stromquelle.
|
|
Vergleich verschiedener
Erklär-Methoden des Energietransports in einem einfachen
elektrischen Stromkreis
|
Damit sich der Lehrer klar wird, was hinter gängigen schulischen Argumentationen im Zusammenhang mit dem Stromkreis steckt, habe ich einen Versuch unternommen, verschiedene Zugänge zum Verständnis des Stromkreises zu analysieren. Anlass sind problematische Äußerungen in der derzeitigen didaktischen Literatur. Ich halte es für sehr nützlich, wenn der Lehrer hier Bescheid weiß. Aber in der Regel sollten die folgenden, detaillierten Überlegungen weder in der Schule noch im Zusammenhang mit Anwendungssituationen explizit angestellt werden.
1. Zugrundeliegende Stromkreise
Für den elektrischen Gleichstrom-Kreis stelle ich mir für das Folgende einen Stromkreis mit Batterie, Widerstand und zwei widerstandslosen Stromzuführungen vor. In solchen Stromzuführungen gibt es kein elektrisches Feld; das sieht man auch am ohm'schen Gesetz in der Form j = σ·E mit der Stromdichte j und der Leitfähigkeit σ (σ => ∞). Das elektrische Feld E außerhalb steht also auf der Wandung senkrecht. Wenn im Inneren E = 0, und wenn dort ein Potenzial φ existiert, ist dieses konstant (E = - grad φ). Ladungsträger in diesem Bereich haben dann das Potenzial des jeweiligen Anschlusses der Batterie. Das ohm'sche Gesetz j = σ·E für die Stromdichte betrifft das innere elektrische Feld E im Leiter. Das gibt es in diesem Fall im Widerstand, parallel zur Stromdichte j = σ·E, und bei einem dünnen Leiter der Geometrie des Leiters folgend, also parallel zur Wandung des Widerstands. Dieses elektrische Feld entsteht beim Einschaltvorgang, wenn der Stromkreis geschlossen wird, aus dem elektrischen Feld der Stromquelle unter dem Einfluss von mitentstehenden Oberflächenladungen (Mantelladungen und Raumladungen an den Übergangsstellen unterschiedlicher Leitfähigkeit), die sich der einsetzende Strom selbst schafft. Schematisch zeigt das Abb. 1.
 |
Die beiden widerstandslosen und damit
feldfreien Stromzuführungen liegen auf den konstanten Potenzialen
der Batterieklemmen. Beim Eintritt in den Widerstand wird in einem
sehr kleinen Übergangsbereich ein linearer Feldanstieg bzw. -abfall
angenommen. Im Inneren des Widerstands mit dem konstanten
elektrischen Feld verändert sich das Potenzial linear, dagegen in
den beiden Übergangsbereichen parabelförmig. Dem Potenzialverlauf entspricht auch die potenzielle Energie eines Leitungs-Elektrons (L-Elektrons), jedenfalls außerhalb der Stromquelle. |
| Abb. 1: Schematische Darstellung von Feld- und Potenzialverlauf (außerhalb der Stromquelle) in einem Stromkreis mit 2 widerstandslosen Stromzuführungen und einem Widerstand | |
Beim Gleichstromkreis muss die Vorgeschichte erwähnt werden: In sehr kurzzeitigen ("mit quasi Lichtgeschwindigkeit") und schwer zu überschauenden Vorgängen bilden sich nach dem Schließen des Stromkreises als Folge des einsetzenden Stroms zunächst Oberflächenladungen (Mantelladungen und Raumladungen) mit zugehörigen elektrischen Feldern innerhalb und außerhalb der Leiter, bis allmählich Kontinuitätsgleichung und Ohm'sches Gesetz (j = σ·E mit der Leitfähigkeit σ) erfüllt sind. Es bildet sich ein stationärer Strom aus mit den zugehörigen stationären Feldern und dem Potenzialverlauf (des Feldanteils außerhalb der Stromquelle), schematisch nach Abb. 1. Die schulische Behandlung setzt - vernünftigerweise - erst danach ein. Auch danach geht alle Wirkung primär von der Stromquelle aus. Oberflächenladungen passen das elektrische Feld an. Die Felder E und B übernehmen eine Vermittlerrolle.
Dieser Gleichstrom-Kreis wird verglichen mit einer Induktionsschleife aus einem homogenen Draht endlicher Leitfähigkeit (Abb. 2; gelb). Er schließt eine Fläche ein, die von einem sich zeitlich ändernden Magnetfeld B' durchsetzt ist. Nach dem Induktionsgesetz entsteht ein elektrisches Wirbelfeld E, das den Leiter der Induktionsschleife begleitet. Es verrichtet im Widerstand Arbeit, die in innere Energie umgewandelt wird. Nicht sehr verschieden davon wäre eine Induktionsschleife mit einem diskreten Widerstand und einer widerstandslosen Verbindung der beiden Enden des Widerstands.
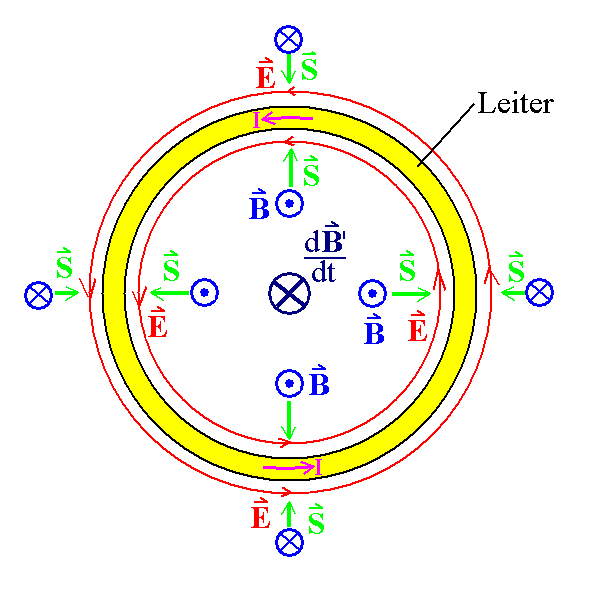 |
Ein sich änderndes magnetisches Feld B' durchsetze einen homogenen Leiterring mit Widerstand (gelb). Es umgibt sich mit einem induzierten elektrischen Wirbelfeld E, das den Leiterring außerhalb und in seinem Inneren begleitet. Es ist je nach dem Vorzeichen von dB'/dt im oder gegen den Uhrzeigersinn gerichtet. Der resultierende Induktionsstrom mit der Stromdichte j erzeugt ein sekundäres Magnetfeld B. Es gibt hier keine Pole, kein Potenzial und keine potenzielle Energie der Elektronen. Es gibt eine (Ring-)Spannung. Sie kann nicht als Potenzialdifferenz gedeutet werden. Dennoch ist die Situation hier fast genauso wie beim Gleichstromkreis, mit dem einzigen Unterschied: Das elektrische Wirbelfeld ist nicht auf die Batterie beschränkt, sondern begleitet die ganze Leiterschleife. Das sekundäre Magnetfeld B (nicht das induzierende Magnetfeld B'), das der Induktionsstrom mit der Stromdichte j erzeugt, ändert sich mit der Richtung sowohl von E als auch von j. Deshalb zeigt der Energiestromdichte-Vektor S immer in den Leiter hinein. Der Energiestromdichte-Vektor S ist ein Vektor senkrecht zu E und senkrecht zu B an einer bestimmten Stelle (Poynting-Vektor). Er zeigt die Richtung an, längs der an dieser Stelle Energie transportiert wird. S kann nur dort von 0 verschieden sein, wo beide Feldstärken von 0 verschieden und nicht parallel sind (Kreuzprodukt). Das induzierte elektrische Feld E verrichtet Arbeit, durch die die innere Energie der Leiterschleife erhöht wird. Dazu ist das Feld in der Lage, weil ständig Energie längs des Energiestromdichte-Vektors S zugeführt wird. Diese Arbeit hängt mit der Definition der Ringspannung über die Arbeit für einen vollen Umlauf zusammen: Spannung ist Arbeit für den Transport einer Ladungsmenge Q bezogen auf die Ladungsmenge, im Falle der Ringspannung auf einem geschlossenen Weg im Inneren des Leiters. |
| Abb. 2: Energiestromdichte-Vektor S bei einer homogenen Induktionsschleife mit Widerstand |
Für diesen Text benenne ich drei verschiedene Methoden, in die z.T. auch einfache didaktische Modelle eingeordnet werden können:
1. Methode: "naiv lokal": Die potenzielle Energie ist lokal an Elektron gebunden (ohne Bezug auf elektrisches Feld); s. unten
didaktische Modelle: z.B. das "Bienen-Nektar-Modell" oder das "Rucksack-Modell" (B-N-M bzw. R-M);
2. Methode: "lokales Feld"-Konzept: a) Das E-Feld
verrichtet Arbeit bzw. b) die Ladungsträger haben nach dem
Einschaltvorgang an einer bestimmten Stelle im elektrischen Feld eine
potenzielle Energie (lokale potenzielle Energie)
didaktische Modelle: u.a. Modelle der Oberflächenladungstheorie; auch das "Aufzug-Rutsche-Modell" (A-R-M z.B. nach Galileo) lässt sich notfalls hier einordnen
3. Methode: "Poynting-Konzept" (nach der Elektrodynamik): Der Energiestromdichte-Vektor S sorgt jeweils für die benötigte Energie, damit das stationäre elektrische Feld E Arbeit verrichten kann.
Im Folgenden werden die Erklär-Methoden hinsichtlich ihrer Tragweite für den einfachen elektrischen Stromkreis untersucht:
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| Leitungselektronen (L-Elektronen) erhalten durch die Stromquelle /
Energiequelle potenzielle Energie, die sie im Widerstand abgeben und
damit dessen innere Energie erhöhen. |
Von der Stromquelle / Energiequelle gehen elektrische Felder aus,
die durch Oberflächenladungen (Raumladungen und Mantelladungen) so
modifiziert werden, dass in dünnen Leitern das E-Feld
konstant ist und der Leitergeometrie folgt. a) Im Widerstand kann E Arbeit verrichten, die die innere Energie erhöht. b) Im elektrischen Feld haben die L-Elektronen an einem bestimmten Ort eine potenzielle Energie, die sie im Widerstand abgeben. |
Während des kurzzeitigen Einschaltvorgangs bilden sich mit Hilfe
von Oberflächenladungen stationäre Werte der Stromdichte j
und vom elektrischen und magnetischen Feld aus (E, B).
Energie strömt außerhalb der Leiter, aber in ihrer Nähe, in Leiter
und Widerstand längs des Energiestromdichte-Vektors S ein. E, B und S breiten sich dabei "quasi mit Lichtgeschwindigkeit" aus. |
2. "Plötzliche" Wirkung beim Einschalten?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Erklärung: da sich Ladungsträger mit nur geringer Driftgeschwindigkeit bewegen. Sie haben keine Zeit, um Energie von der Batterie abzuholen und auch nicht, um "leer" zur Batterie zurück zu laufen. |
"Plötzlich": Während des kurzzeitigen Einschaltvorgangs a) entstehen solche E-Felder, die Arbeit verrichten können bzw. b) sammeln "alle" L-Elektronen in der negativen Stromzuführung im Vergleich zur positiven Stromzuführung potenzielle Energie auf. Den Potenzialverlauf und die zugehörige potenzielle Energie der Ladungsträger zeigt Abb. 1. Der Einschaltvorgang "geschieht (fast) mit Lichtgeschwindigkeit". |
"Plötzlich": Während des kurzzeitigen Einschaltvorgangs bilden
sich die stationären Werte von E, B und S
aus. E, B und S breiten sich dabei "quasi mit Lichtgeschwindigkeit" aus. |
3. Woher kommt die Pumpenwirkung für die Ladungen?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| unklar: vielleicht irgendwie durch Coulombabstoßung der Elektronen vom negativen Pol und Anziehung durch den positiven Pol? |
Primär von der Stromquelle unter Mitwirkung elektrischer Felder,
die von der Stromquelle ausgehen, aber durch Oberflächenladungen
modifiziert werden; im A-R-M durch den Höhen-Unterschied simuliert |
Primär von der Stromquelle unter Mitwirkung/Vermittlung elektrischer Felder, die aber durch Oberflächenladungen modifiziert werden. Auch magnetische Felder, die der Strom sich erzeugt, wirken / vermitteln mit. |
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Pumpenwirkung mehr vorhanden,
"Lücke müsste überwunden werden" |
keine Pumpenwirkung für Ladungen mehr vorhanden; jedoch noch kurzzeitige, wohl belanglose "Trägheitsbewegung"; währenddessen und danach neuer Einstellvorgang eines stationären Zustands der Ladungen, Felder und Potenziale; danach keine Arbeit mehr; auf allen zusammenhängenden Teilen des Stromkreises herrscht gemeinsames Potenzial; Offen: Woher hat E die Energie, damit Arbeit
verrichtet werden kann? Wohin verschwindet diese bei einer
Unterbrechung? |
Nach der belangslosen, kurzzeitigen "Trägheitsbewegung": Es werden keine Ladungen zur Bildung eines Stroms (j) nachgeliefert, so verschwinden auch B und damit S . |
5. Woher kommt die Energie, die das elektrische Feld veranlasst, Arbeit im Widerstand zu verrichten?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| für das Modell belanglos | Unklar: Jedenfalls nicht von den stationären
Oberflächenladungen, die beim Einschaltvorgang entstanden sind. Ein Potenzialfeld statischer Ladungen kann nämlich nicht dauernd Arbeit verrichten! |
Die Energie kommt von der Stromquelle / Energiequelle und strömt längs S außerhalb, aber nahe beider Stromzuführungen in den Widerstand. |
6. Wohin geht die Energie der Ladungen bei Unterbrechung des Stromkreises?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| Eine noch stattfindende "Trägheitsbewegung" der Ladungen,
während der noch kurzzeitig potenzielle Energie an den Widerstand
abgegeben wird, ist wohl unerheblich. Nicht erklärt: Wohin geht die potenzielle Energie der Mehrheit der Ladungen? |
Während der kurzzeitigen "Trägheitsbewegung" nach der
Unterbrechung wird noch potenzielle Energie abgegeben bzw. Arbeit
verrichtet bis in den Leitern E = 0. Nicht erklärt: Wohin geht die potenzielle Energie der Mehrheit der Ladungen? |
Da S = 0, wird keine Energie mehr nachgeliefert. Ob
vorher die Ladungen Energie hatten, ist unerheblich. |
7. Warum sind beide Leitungen energetisch gleichwertig?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| scheinbar nicht gleichwertig: Es sieht so aus, als würde auf einer Leitung Energie geliefert, während die andere Leitung energetisch keine Funktion hat. |
Siehe Wechselstrom! Immer unterscheiden
sich beide Leitungen hinsichtlich der Energie, aber jeweils
anders. In beiden Phasen des Wechselstrom gibt es Arbeit und
Energiezufuhr durch jeweils eine Leitung an den Widerstand. |
E und B bestimmen auf beiden Leitungen
gleichzeitig ein gleichgerichtetes S, auch bei
Wechselstrom. Längs beider Leitungen strömt Energie in den Widerstand - gemäß S. |
8. Woher "weiß" ein Elektron, dass es im einzigen Widerstand seine ganze Energie abgeben soll (und nicht etwa einen Teil zurückhalten soll für einen evtl. in Reihe geschalteten Widerstand)?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Erklärung | Je nach Größe der elektrischen Felder
in den Widerständen wird Arbeit verrichtet. (Mit potenzieller Energie schwerer zu erklären.) |
Es gibt keine weitere Möglichkeit,
Arbeit zu verrichten. Im Einschaltvorgang haben sich die Felder
und Ladungen auf die vorliegende stationäre Situation mit einem
Widerstand eingestellt. |
9. Woher "kennen" Elektronen die Spannungs-, Feld- und Energieverteilung bei einer Reihenschaltung?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Erklärung |
E-Felder stellen sich in der Einschaltphase so ein (so etwas wie ein "Fließgleichgewicht" )! Der Strom hat sich die stationären Werte selbst geschaffen. | E-Felder stellen sich in der Einschaltphase so ein
("Fließgleichgewicht")! Der Strom hat sich die stationären Werte
selbst geschaffen. Darauf baut S auf. |
10. nichtlokale Vorgänge (Potenzialdifferenz, E)
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Erklärung | Vorgeschichte der Einschaltphase spielt eine Rolle | Das Konzept setzt E und B voraus, evtl. entstanden in der kurzen Einschaltphase. Darauf baut S auf. Betrachtung von Potenzialen und Potenzialdifferenzen ist hier überflüssig und problematisch. |
11. Warum strömt Energie in zwei parallel geschaltete Widerstände?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| An einem Ende beider Widerstände haben Elektronen gleiche
potenzielle Energie, die jeweils an den Widerstand abgegeben wird. |
E-Felder verrichten in beiden Widerständen Arbeit / bzw. an einem Ende beider Widerstände haben Elektronen gleiche potenzielle Energie entsprechend der Spannung der Energiequelle | E und B bestimmen bei beiden Widerständen S |
12. Wenn Elektronen potenzielle Energie haben, warum geben sie diese bei Unterbrechung des Stromkreises nicht weiter ab?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| Eine noch stattfindende "Trägheitsbewegung" der Ladungen,
während der noch kurzzeitig potenzielle Energie an den Widerstand
abgegeben wird, ist wohl unerheblich. Das machen sie noch kurzzeitig während der "Trägheitsbewegung, aber nicht alle Elektronen in der Stromzuführung. Was geschieht mit dem Rest? keine Erklärung |
Einige geben sie noch kurzzeitig während der "Trägheitsbewegung"
ab, aber nicht alle Elektronen in der Stromzuführung. Felder
ändern sich mit der Unterbrechung, sodass geändertes Potenzial und
andere potenzielle Energie entsteht (Umordnungsvorgang). Was geschieht mit dem evtl. Rest der Energie? |
keine Aussage; betrifft dieses Modell nicht |
13. Was geschieht bei einem zeitlich veränderlichen Gleichstrom?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| Unklar: Bemerken die Elektronen etwa instantan, dass sich die Spannung etc. geändert hat? Wie erhalten die unterwegs befindlichen Elektronen geänderte potenzielle Energie? |
Wenn Spannung und Strom langsam veränderlich sind im Vergleich
zum Zeitverlauf des jeweiligen Anpassungsvorgangs, sind die Felder
quasistationär. Der Leitungsstrom schafft sich seine notwendigen
Felder in kurzer Zeit jeweils selbst (Oberflächenladungs-Theorie).
Schwierige Beurteilung, wie sich die potenzielle Energie der L-Elektronen im jeweils geänderten E-Feld mitverändert. Beim A-R-M veränderliche Hubhöhe des Aufzugs simuliert unterschiedliche Spannung. |
S ändert sich mit E, j und B. Geänderte Energie (Fähigkeit, Arbeit zu verrichten) steht im Widerstand "schnell" zur Verfügung ("mit quasi Lichtgeschwindigkeit"; quasistationärer Zustand). |
14. Energietransport bei Wechselstrom?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| keine Erklärung, Die Laufstrecke der Elektronen ist durch die halbe Periodendauer begrenzt. Nach dem Modell haben die Elektronen in einer halben Periode in der Regel keine Zeit, um Energie von der Stromquelle "abzuholen". |
Man kann nur spekulieren! Der Leitungsstrom verändert zu jedem Zeitpunkt Oberflächenladungen und Felder in einem schwer überschaubaren intermediärer und extrem kurzzeitigen Einstellvorgang so, dass das quasistationäre E-Feld die jeweils "richtige" (?) Arbeit verrichten kann. Der Leitungsstrom schafft sich seine notwendigen Felder selbst. Das jeweils geänderte E-Feld verrichtet sodann - evtl. nach Umpolung auf einem jeweils anderen Weg - Arbeit. Fragen, die ich mit dieser Methode nicht beantworten kann: Wie kommt die Energie, mit der das E-Feld Arbeit verrichtet, von der Energiequelle an den Widerstand? Noch schwierigere Erklärung mit potenzieller Energie, weil nämlich jeweils andere Elektronen (in Stromzuführung A oder B) im geänderten E-Feld nach dem Modell positive potenzielle Energie haben, die sie an den Widerstand abgeben. Wohin geht die Energie der Ladungen bei Richtungswechsel? Woher kommt sie? Umsteuerung der Energie unklar! |
Unabhängig von der Stromrichtung zeigt S immer von der
Energiequelle zum "Verbraucher". Wie E und B bei einer jeden Stromrichtung entstehen (intermediärer Einstellvorgang bzw. Umordnungsvorgang), wird nicht betrachtet. Das scheint irrelevant zu sein, wenn es genügend schnell erfolgt. |
15. Strom in einer Induktionsschleife?
| Erklär-Methode: | "naiv lokal" | "lokales Feld"-Konzept | Poynting-Konzept |
| Eine andere Theorie ist nötig, weil das Konzept des
Gleichstromkreises nicht anwendbar ist, da hier keine potenzielle
Energie existiert. Spannung als Potenzialdifferenz funktioniert hier nicht, da i.A. kein Potenzial existiert. |
Epot nicht anwendbar, da keine potenzielle Energie
existiert. Durch Arbeit Erhöhung der inneren Energie des Widerstands bei beiden Orientierungen des elektrischen Felds. Aber Arbeit jeweils unterschiedlich je nach Richtung von E. Bei beiden Richtungen des Induktionsstroms nimmt die innere Energie des Widerstands zu. |
Epot nicht anwendbar, da keine potenzielle Energie
existiert. E-Feld und B-Feld vom Induktionsstrom j sind beide in jeder Phase unterschiedlich orientiert, aber so, dass S jeweils gleich orientiert ist (Abb. 2); wie beim Gleichstromkreis; jedoch E durch Induktion erzeugt und nicht durch Oberflächenladungen beim Einschaltvorgang. Diese schafft sich der Induktionsstrom zusätzlich selbst. |
Das Fahrradketten-Modell (F-K-M) ist ein eigenes Modell mit gewissen Ähnlichkeiten zu einem "lokalen Feld"-Modell. Es macht im unverzweigten Stromkreis plausibel, dass der Strom immer im Kreis fließt. Man kann sich aber auch vorstellen, dass damit überhaupt einsichtig gemacht wird, dass Energie transportiert wird. Wie der Energietransport von der Quelle zum "Verbraucher" funktioniert, bleibt offen. Schwierig ist eine Erklärung der Vorgänge bei in Reihe geschalteten Widerständen, unmöglich bei parallel geschalteten Widerständen.
Ähnliches gilt für das Starrer-Elektronenring-Modell (S-R-M).
Beim A-R-M kann durch variierende Aufzugshöhe unterschiedliche potenzielle Energie simuliert werden.
Problematisch ist bei auf der potenziellen Energie beruhenden Modellen, dass ein reines Potenzialfeld nicht die nötige Energie für einen dauernden Strom heranschaffen kann.
Mit dem Pumpenmodell (bzw. dem Modell des geschlossenen Heizstromkreises; vgl. Arbeitsblatt Vergleich) lassen sich die dominierende Rolle der Stromquelle / Energiequelle, die Tatsache des ungeschwächten Kreisstroms, die Bedeutung des Energietransports, gekoppelt an den Strom, und die Irrelevanz von potenziellen Energien dabei gut veranschaulichen, wenn der Lehrer darauf verzichtet, mit dem Druck zu argumentieren. Die Rohrleitungen mit ihrer starren Form sorgen dafür, dass der Wasserstrom der Rohrgeometrie folgt. Die mechanischen Kräfte in den Wänden der Rohrleitungen entsprechen so den elektrischen Kräften infolge der Oberflächenladungen und dem von ihnen verformten elektrischen Feld. Sie sollten m.E. wie diese bestenfalls am Rande im Schulunterricht erwähnt werden. Das Pumpenmodell hat eine gewisse Ähnlichkeit zu einem "lokales Feld"-Konzept. Anders als im elektrischen Stromkreis wird hier die Energie "in den Leitungen" (eng gebunden an das strömende Wasser) transportiert.
4. Im Folgenden wird ins Gedächtnis gerufen, wie nach dem Standard-Modell
der Elektrodynamik Energie aus der Energiequelle/Stromquelle
in den Widerstand transportiert wird.
 |
 |
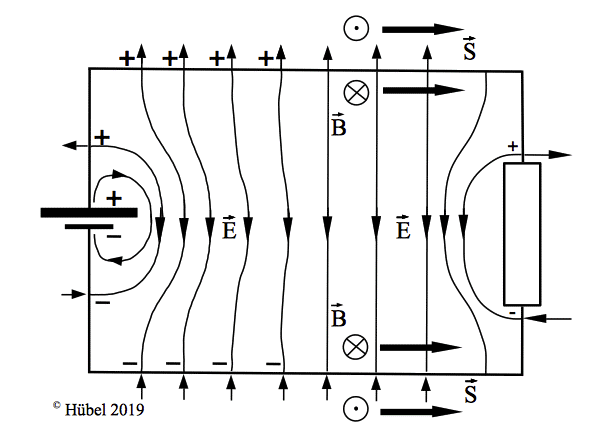
| Abb. 3: Energietransport aus der
Batterie in den Widerstand, vermittelt durch elektrische und
magnetische Felder (E und B) gemäß des
Energiestromdichte-Vektors S überwiegend in der Nähe
beider Leiter. Wegen E = 0 in den widerstandslosen
Stromzuführungen, ist dort S = 0: Durch sie fließt keine
Energie, wohl aber in der Nachbarschaft, wo E =/= 0 und
B groß ist. |
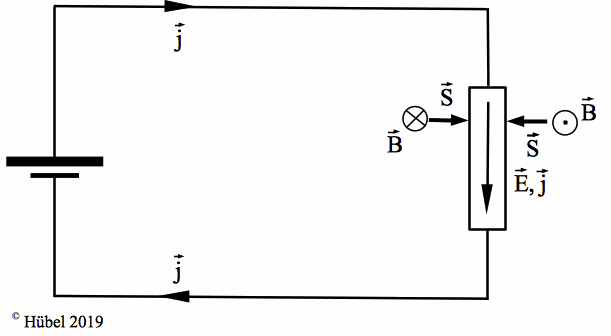
Abb. 4: Energiestrom durch die Wandung in den Widerstand, aus dem Vakuum (bzw. der Luft) vor allem in der Nähe beider Stromzuführungen kommend. Der Strom erzeugt sich das Magnetfeld B selbst. |
Frage: Könnte man in der Schule nicht den Energiestromdichte-Vektor S - nichtformalisiert und nur qualitativ - einführen, um die Energietransportvorgänge beschreiben zu können? Lediglich Mitteilung: S ist ein Vektor, der immer senkrecht zu E und B steht?
Grob gesagt sollen Elektronen im Widerstand nahe des negativen Pols ihre potenzielle Energie abgeben und ohne diese zum positiven Pol zurück fließen. Das scheint intuitiv sehr einsichtig.
In einer Zeit t wird durch einen Strom I eine Ladungsmenge Q = I·t transportiert. Bei einem zylinder- bzw. drahtförmigen Widerstand mit der Elektronendichte n, und der Querschnittsfläche A sind das alle Ladungen, die in einem Zylinder der Querschnittsfläche A und der Länge 𝓁 = vD·t enthalten sind, wenn vD die Driftgeschwindigkeit in der Größenordnung von 1 mm/s ist. Es sind also N = n·A·𝓁 = n·A·vD·t Elektronen beteiligt, die die Ladung Q = -e·n·A·vD·t transportieren (also I = -e·n·A·vD). Dabei wird die potenzielle Energie Q·U = -e·N·U abgegeben, pro Elektron also -e·U.
(Die Drude-Theorie macht dann noch die zusätzliche Aussage vD = e·λ/(2·m·vth)·E mit der mittleren freien Weglänge λ und dem Betrag der mittleren thermischen Geschwindigkeit vth. Diese bestimmt die mittlere Stoßzahl.)
Daran ist nichts auszusetzen, wenn man sich nicht vorstellt, dass jedes dieser Elektronen seine potentielle Energie direkt vom negativen Pol der Stromquelle / Energiequelle "abholen" muss.
Aber bei dieser Betrachtungsweise bleibt offen: Woher haben die Elektronen ihre potenzielle Energie? Die Elektronen, die ihre Energie im Widerstand abgeben, waren in der Regel nie nahe der Energiequelle/Batterie und konnten "sich nie dort ihre Energie abholen". Bereits die Methode "lokales Feld" erklärt, dass sie diese tatsächlich lange vorher, durch den Einschaltvorgang mit der Bildung von Oberflächenladungen und dem sich einstellenden elektrischen Feld erhalten haben.
Bei der Induktionsschleife muss es sowieso anders sein, da dort keine potenzielle Energie existiert. Aber durch Induktion entsteht ein elektrisches Feld im Leiter und seiner Umgebung. Es kann Arbeit verrichten.
Problem der lokalen Deutung: Woher hat ein L-Elektron seine
potenzielle Energie, obwohl es in der Beobachtungszeit nie nahe eines
Pols war?
In einem ausgedehnten Leiter, z.B. einem elektrolytischen Trog, folgen Stromdichte und elektrische Feldstärke nicht der Geometrie des Leiters. Aber egal, ob das E-Feld der Leitergeometrie folgt oder nicht: Zur Verschiebung zwischen zwei Punkten ist bei Existenz eines Potenzials immer die gleiche Arbeit nötig, unabhängig vom Weg.
In der Schule kann man m.E. - wenn man unbedingt mit einem Potenzial arbeiten möchte - die Argumentation mit einer Potenzialdifferenz (verbal) vereinfachen, wenn man vom "Potenzial im Vergleich zu ... " (einem bestimmten Punkt) spricht, wie es ja auch in der Elektronik üblich ist, wo immer nur "das Potenzial" (gemeint: im Vergleich zur "Masse", dem Potenzialnullpunkt) diskutiert wird. Ich denke, hierin liegt nicht die größte Schwierigkeit des elektrischen Stromkreises. Bereits beim freien Fall argumentiert man ja mit der "potenziellen Energie" und meint z.B. "potenzielle Energie im Vergleich zum Erdboden". Der Gebrauch eines Potenzials beim Stromkreis hat jedoch die u.a. in diesem Artikel besprochenen Nachteile. Ansonsten gewinnt man m.E. nichts für das Verständnis der Spannung, wenn man sie Potenzialdifferenz nennt (vielleicht, außer dass man sich als "Fachmann" outet).
Die Stromdichte j ist ein Vektor, der in Flussrichtung der stromtransportierenden Ladungen zeigt (bei positiven Landungen, andernfalls entgegengesetzt; j = ρ·v; hier ρ Ladungsdichte, v Geschwindigkeit der Ladungsträger). Sein Betrag ergibt sich aus der durchströmten Fläche A und der Stromstärke I durch A, also |j| = I/A.
Die Leitfähigkeit σ ist der Kehrwert des
spezifischen Widerstands ρ.
( Oktober 2019 )