Der Freie Fall ist eine idealisierte Bewegung, die Galilei, der
Legende nach, beim Fall eines Steins vom schiefen Turm von Pisa als erster
untersucht haben soll.
Der Stein fällt beschleunigt, weil auf ihn die Gewichtskraft FG
nach unten wirkt. Der Vorgang heißt Freier Fall, wenn
die Gewichtskraft die einzig wirkende Kraft ist, bzw., wenn andere Kräfte
vernachlässigbar sind. In Realität wirkt in der Regel die
Luftreibungskraft FR, die beim Fall
entgegengesetzt zur Bewegungsrichtung, und hier auch der Gewichtskraft,
orientiert ist. Streng genommen gibt es also in der Luft keinen Freien
Fall. Aber bei nicht zu großer Fallhöhe bzw. nicht zu großer
Fallgeschwindigkeit kann man einen realen Fall in guter Näherung als
einen Freien Fall behandeln. Experimente zeigen dann auch in guter
Näherung die Eigenheiten eines Freien Falls. Ein idealer Freier Fall
würde Vakuum erfordern, wie es z.B. auf dem Mond herrscht, oder im Bremer
Fall-Turm.

|
Abb. 1: Schulexperiment zum Freien Fall mit Zackenkamm
("g-Leiter") und Lichtschranke: Versuchsdurchführung.
Wenn der Zackenkamm (rot) durch den Lichtstrahl
der blauen Lichtschranke fällt, wird der Lichtstrahl unterbrochen
und anschließend wieder frei gegeben.
Ein PC mit angeschlossener Elektronik registriert jeweils die Zeit t
seit der ersten Unterbrechung. Bei bekanntem Sprossenabstand ist
dann auch die Position x des Zackenkamms dem PC bekannt.
Der PC stellt dann ein t-x-Diagramm dar, oder, da er auch die Momentangeschwindigkeit
mit registriert, ein t-v-Diagramm*).
Das Programm stellt verschiedene Auswertungsmöglichkeiten zur
Verfügung, mit denen z.B. die Steigung des Diagramms zur Messung der
Fallbeschleunigung ermittelt werden kann.
|
|
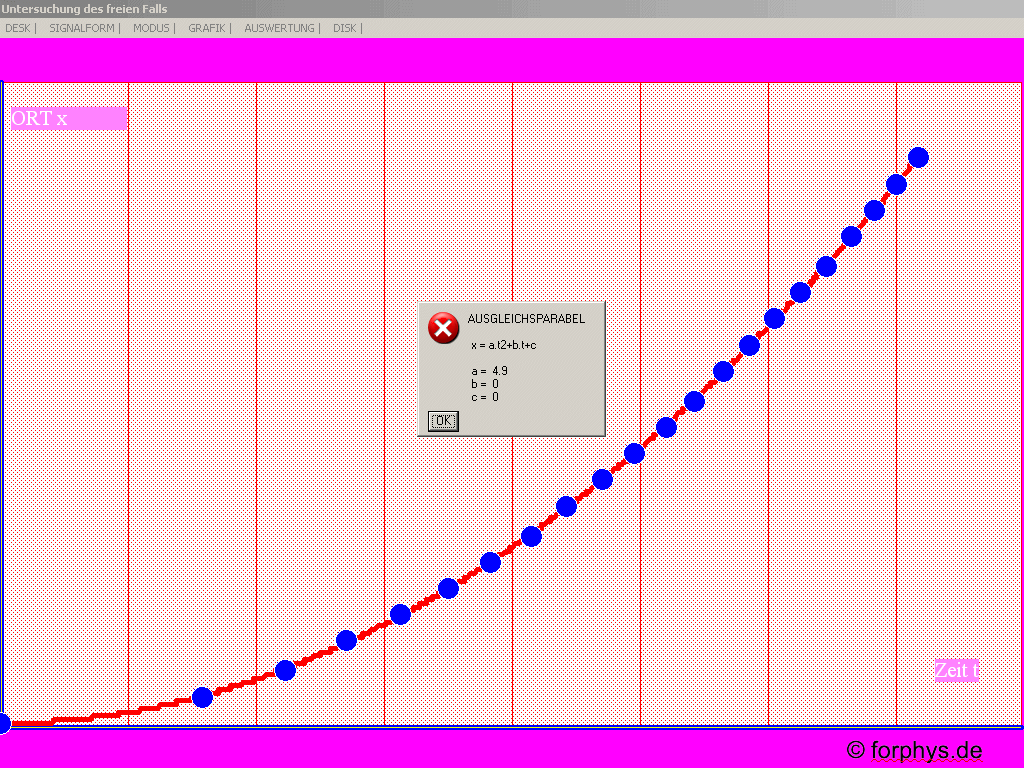
Abb. 2: Schulexperiment zum Freien Fall mit Zackenkamm und
Lichtschranke - t-x-Diagramm.
Wenn man den Zackenkamm kurz vor der ersten Unterbrechung loslässt,
erhält man ein t-x-Diagramm, das sehr überzeugend nach einer Parabel
aussieht.
Dass es wirklich eine Parabel ist, kann bestätigt werden (Abb. 5). |
|
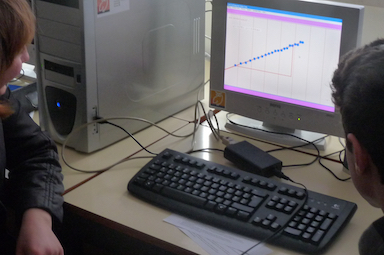
Abb. 3: Schulexperiment zum Freien Fall mit Zackenkamm und
Lichtschranke: t-v-Diagramm.
Das Programm, das die Daten der Lichtschranke verarbeitet, kann
daraus auch die momentane Fallgeschwindigkeit ermitteln. Daraus
ergibt sich als t-v-Diagramm eine Gerade, die bei exaktem Start aus
der Ruhe eine Ursprungsgerade ist.
Dass das t-v-Diagramm eine Gerade ist, bestätigt, dass die
Beschleunigung (Steigung des t-v-Diagramms) konstant ist.
Auf dem Foto links startete der Zackenkamm offenbar mit einer
Anfangsgeschwindigkeit v0 infolge einer größeren
Starthöhe. Mittels des eingezeichneten Steigungsdreiecks kann die
Fallbeschleunigung g jedoch auch in diesem Fall ermittelt werden.
(Das kleine schwarze Kästchen ist das Steuergerät für die
Lichtschranke, das die Daten zur Verarbeitung und Darstellung an
den PC liefert.) |
|
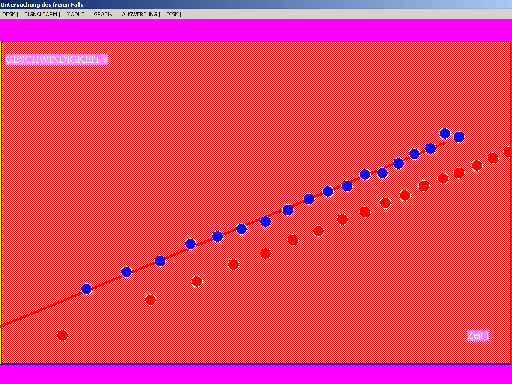
Abb. 4: Schulexperiment zum Freien Fall mit Zackenkamm und
Lichtschranke: t-v-Diagramm.
Bei unterschiedlichen Starthöhen hat der Zackenkamm beim ersten
Unterbrechen der Lichtschranke unterschiedliche
Anfangsgeschwindigkeit.
Dass alle t-v-Diagramme dennoch parallel verlaufen (gleiche
Steigung) bestätigt, dass die Fallbeschleunigung g
unabhängig von der Starthöhe ist.
Im Fall der blauen Punkte startete der Zackenkamm offenbar mit einer
Anfangsgeschwindigkeit infolge einer größeren Starthöhe. Mittels des
einzuzeichnenden Steigungsdreiecks kann die Fallbeschleunigung g
ermittelt werden. |
|
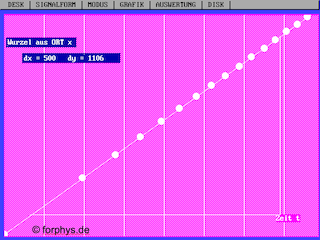
Abb. 5: Schulexperiment zum Freien Fall mit Zackenkamm und
Lichtschranke - verarbeitetes t-x-Diagramm.
Bei exaktem Start aus der Ruhe ergibt sich für die Wurzel aus dem
Ort x eine Ursprungsgerade. Sie bestätigt die quadratische
Abhängigkeit des Orts x von der Zeit t.
Auch aus der Steigung dieses Diagramms könnte die Fallbeschleunigung
g ermittelt werden. |
Zur Theorie des Freien Falls: siehe hier.
Die Registrierung eines t-v-Diagramms für eine
gleichmäßig beschleunigte Bewegung zeigt eine lineare Funktion für das
t-v-Diagramm. Das führt zur Definition der Beschleunigung
a
Bremer-Fallturm: Es handelt sich um einen
146 m hohen Turm in Bremen zum Studium der Schwerelosigkeit. In einer
120 m langen Röhre herrscht Vakuum, das den Freien Fall einer Kapsel mit
0,8 m Durchmesser und ca. 2 m Höhe ermöglicht. Von der Erde aus gesehen,
wirkt immer die Gewichtskraft. Aber vom Inneren der Fallkapsel aus
gesehen herrscht während der ca. 5 s des Freien Falls Schwerelosigkeit.
Man kann die Kapsel auch zunächst von unten nach oben katapultieren.
Dann verdoppelt sich die Zeit der Schwerelosigkeit.
*) Messung der Momentangeschwindigkeit
nach der Zeitmittenmethode
Der Zackenkamm kann nach Abb. 1 aus einem
Stück Fotokarton hergestellt werden, beidseitig mit selbstklebender
Folie verstärkt und so und mit Tesafilmstreifen an den losen Enden der
"Zacken" gegen "Flattern" etwas stabilisiert. Es gibt auch
Lehrmittelfirmen, die einen Zackenkamm unter dem Namen "g-Leiter"
anbieten.
.
( November 2020)




