Der Freie Fall ist eine idealisierte Bewegung,  die Galilei, der Legende nach, beim Fall eines Steins vom schiefen Turm von Pisa als erster untersucht haben soll.

Der Stein fällt beschleunigt, weil auf ihn die Gewichtskraft F_G nach unten wirkt. Der Vorgang heißt Freier Fall, wenn die Gewichtskraft die einzig wirkende Kraft ist, bzw., wenn andere Kräfte vernachlässigbar sind. In Realität wirkt in der Regel die Luftreibungskraft F_R, die beim Fall entgegengesetzt zur Bewegungsrichtung, und hier auch der Gewichtskraft, orientiert ist. Streng genommen gibt es also in der Luft keinen Freien Fall. Bei nicht zu großer Fallhöhe bzw. nicht zu großer Fallgeschwindigkeit kann man einen realen Fall in guter Näherung als einen Freien Fall behandeln. Experimente zeigen dann auch in guter Näherung die Eigenheiten eines Freien Falls. Ein idealer Freier Fall würde Vakuum erfordern, wie es z.B. auf dem Mond herrscht, oder im Bremer Fall-Turm.

Weil F konstant ist, ist es auch die Beschleunigung a, d.h. es handelt sich um eine gleichmäßig beschleunigte Bewegung.

Eine gleichmäßig beschleunigte Bewegung ist eine Bewegung mit konstanter Beschleunigung a bzw. unter der Wirkung einer konstanten Kraft F = m·a . Dabei sind sowohl die Richtung als auch der Betrag des Beschleunigungsvektors  und des Kraftvektors konstant.

Die Beschleunigung a wird hier die Fallbeschleunigung g genannt. Ihr Betrag heißt auch Ortsfaktor g = 9,81 N/kg = 9,81 m/s².  Die Fallbeschleunigung ist unabhängig von der Masse des fallenden Körpers; denn bei doppelter Masse (Trägheit) ist auch die Gewichtskraft  F_G = m·a doppelt so groß. Du kannst das auch mathematisch beweisen:

2. NG:     F = m·a  ; 

andererseits F = Gewichtskraft F_G = m·g, also   m·a = m·g =>   m kürzt sich heraus, und es gilt a = g.

Beides ist hier der Fall.

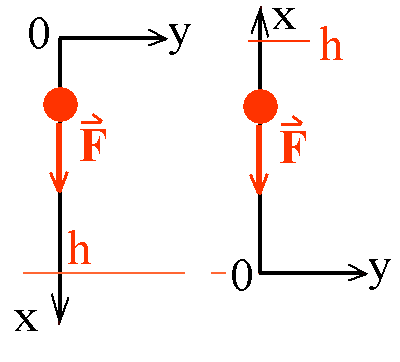
Wahl des Koordinatensystems Diese ist weitgehend willkürlich. Man wählt das Koordinatensystem in der Regel so, dass die Rechnung möglichst einfach wird. Mit (I) und (II) sollen zwei verschiedene Möglichkeiten durchgespielt werden.
	Verschiedene Wahlmöglichkeiten für ein Koordinatensystem:       Links (I), rechts (II)

Nach den Gesetzen der gleichmäßig beschleunigten Bewegung, vereinfacht auf die x-Koordinate, gilt

Wahl (I):

Beim einfachen Freien Fall lässt man einen Gegenstand zur Zeit t = 0 s aus der Ruhe fallen. Er hat dann die Anfangsgeschwindigkeit v₀ = 0. In der Regel legt man den Koordinatenursprung in den Startpunkt (Anfangsort x₀ = 0). Die positive Koordinatenrichtung (x) soll die nach unten orientiert sein. Während des Falls ändert sich x von 0 auf immer größere positive Werte.

Aus (1) und (2) wird hier also (x₀ = 0;  v₀ = 0):

Aufgabe: Nimm an, dir fällt vom Balkon aus der Höhe von 6 m ein Blumentopf auf die Straße. Wenn er vom Koordinatenursprung startete, trifft er auf die Straße bei x = 6 m. Wie lange fällt der Blumentopf? Kann er einen Passanten ernsthaft verletzen? Berechne, um das zu beurteilen, auch die  Geschwindigkeit.

Gegeben:  x = 6 m  (rechne näherungsweise mit g = 10 m/s²)

Gesucht: t und v

(a) Also   t = √(2x/g) = √(12/10)  s = 1,1 s :   ganz schön schnell!

und v = g·t = 10 m/s²·1,1 s = 11 m/s ≈ 39,6 km/h.

Den Blumentopf möchte ich nicht auf den Kopf bekommen!

(b) Wenn du den Blumentopf  nach unten wirfst mit der Anfangsgeschwindigkeit v₀ = 4 m/s, heißen (1) und (2)  jetzt

( v₀  ist positiv, da  die Anfangsgeschwindigkeit in positive Richtung zeigt).

Um die Fallzeit t zu berechnen, musst du jetzt die quadratische Gleichung lösen:

1/2·g· t² + v₀·t - x = 0  . Du kannst das sicher, aber ich möchte dir für den Moment den Rechenweg ersparen. Du erhältst  t =  0,766 s (die negative 2. Lösung spielt keine Rolle). Die Fallzeit ist - wie zu erwarten - kürzer als bei Aufgabe (α).

Damit ergibt sich gemäß (2") eine noch größere Fallgeschwindigkeit beim Aufprall als bei (α): v = 11,7 m/s = 41m/s.

(c)  Du könntest den Blumentopf aber auch noch oben werfen mit der Anfangsgeschwindigkeit v₀ = - 4 m/s. Sie ist negativ, weil sie nach oben in negative Koordinatenrichtung zeigt.

Wie hoch steigt dann der Blumentopf?

Er steigt hoch, bis er zum Stillstand kommt. Also aus (2"):   v = 0 => t =  - v₀/g = 4/10 s = 0,4 s.  Dann hat er den Ort 

x = v₀·t +  1/2·g· t² = - 4 · 0,4 m + 5 · 0,16 m = - 0,8 m erreicht.

Weil die positive Koordinatenrichtung nach oben gerichtet ist, erreicht der Blumentopf einen negativen Ort, nämlich in der Höhe + 0,8 m über dem Startpunkt (= Koordinatenursprung).

Wahl (II):

Du hättest den Koordinatenursprung auch auf dem Boden wählen können. Die positive Koordinatenrichtung wäre dann nach oben orientiert. Dann wäre der Startpunkt am Anfangsort x₀ = 6 m. Alle x-Werte beim Fall wären positiv, aber die Fallbeschleunigung a = -g = - 9,81 m/s² wäre negativ (entgegengesetzt zur positiven Richtung), ebenso die Geschwindigkeiten (nach unten gerichtet). Bei Start aus der Ruhe wäre v₀ = 0 (wie bei der früheren Wahl des Koordinatensystems).

Wir hätten also

also (1'")   x = x₀  - 1/2·g· t²    und   (2'")  v =  - g·t

a) Fallzeit t?  mit g ≈ 10 m/s²;

Am Ende der Fallzeit ist x = 0:

Aus    t²  = 2(x₀ -x) /g = 12/10 s²    => t =  1,1 s;  v = - g·t = - 11 m/s in negative Koordinatenrichtung orientiert, also nach unten;   weiter wie oben

Wegen der hier notwendigen Minuszeichen erscheint die Wahl (II) geringfügig komplizierter als (I).