Elektronische Materie besteht aus verschiedenen Komponenten. Am häufigsten werden (einzelne) Elektronen betrachtet. Bei ihnen misst man immer die Teilchenzahl 1. Nach der Quantenelektrodynamik ist ein Elektron der niedrigste Anregungszustands eines Elektronenfeldes. Es gibt aber auch Elektronenzwillinge und weitere höher angeregte Zustände des Elektronenfelds: Elektronenzwillinge sind verschränkte Elektronenzustände mit einigen wenigen Eigenschaften des Gesamtzustands. Bei ihnen misst man immer die Teilchenzahl 2. Sie bestehen aber nicht aus zwei einzelnen Elektronen, zerfallen jedoch bei Messung von Einelektronen-Eigenschaften in solche unter Einhaltung der Eigenschaften des Gesamtzustands (vgl. Dreiklang verschränkter Zustände).

Für ein einzelnes Elektron ist die Teilchenzahl 1 charakteristisch. Elektronen haben darüber hinaus einige feste/be-stimmte Eigenschaften, wie die Ladung q = -e (e Elementarladung 1,6·10^-19 A·s) und die (Ruhe-)Masse m₀ = 9,1·10^-31kg. Sie haben weiter eine Eigenschaft, die es in der klassischen Physik nicht gibt. In Anlehnung an ähnliche^*)  klassische Eigenschaften wurde für sie der Name "Spin" erfunden. Auch Atome oder andere Quantenteilchen können einen Spin haben.

Entdeckt wurde der Elektronenspin 1922 mit einer "Stern-Gerlach-Apparatur", die nach ihren Erfindern benannt ist. Sie soll hier nur symbolisch dargestellt werden in Form eines hypothetischen  Spin-Messers. Die richtige Deutung durch einen "halbzahligen Spin" erfolgte 1925 durch Goudsmit und Uhlenbeck.

Nach Durchtritt eines Elektronenstrahls bzw. eines Ag-Atomstrahls¹⁾ durch den Spin-Messer erhält man in der Regel genau zwei Strahlen mit jeweils einheitlichem Spinwert, mit denen man weiter experimentieren kann. Man spricht von Strahlen polarisierter Elektronen.

Nach Durchtritt eines einzelnen Elektrons erhält man stets ein eindeutiges von den beiden möglichen Ergebnissen. Man kennt dann den Spin dieses Elektrons nach dem Durchtritt. Bei einem weiteren, in gleicher Weise hergestellten Elektron könnte aber ein anderes Ergebnis entstehen. Nur, wenn man immer wieder misst und das gleiche Ergebnis erhält, kann man davon ausgehen, dass die Elektronen den gemessenen Spin schon vor dem Spin-Messer haben.

Betrachten wir wieder einen Elektronenstrahl mit vielen Elektronen: Wenn aus dem Spin-Messer nur ein Strahl mit einem festen Spin-Wert austritt, kann man davon ausgehen, dass alle Elektronen im Strahl auch schon vorher diesen Spin-Wert hatten. In diesem Fall dient ein Spin-Messer auch zum Messen des Spins vor dem Spin-Messer.

Bei Spin-Messungen an sehr vielen Elektronen erhält man statistisch streuende Werte, jeweils zu typisch 50% der Fälle. Wegen der zwei "Einstell"möglichkeiten³⁾ des Spins wird dieser in den folgenden Zeichnungen immer als Pfeil mit einer der zwei möglichen Richtungen gezeichnet.

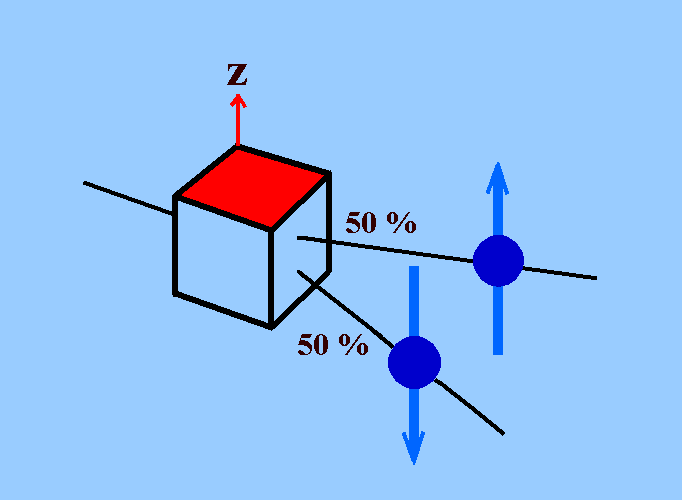
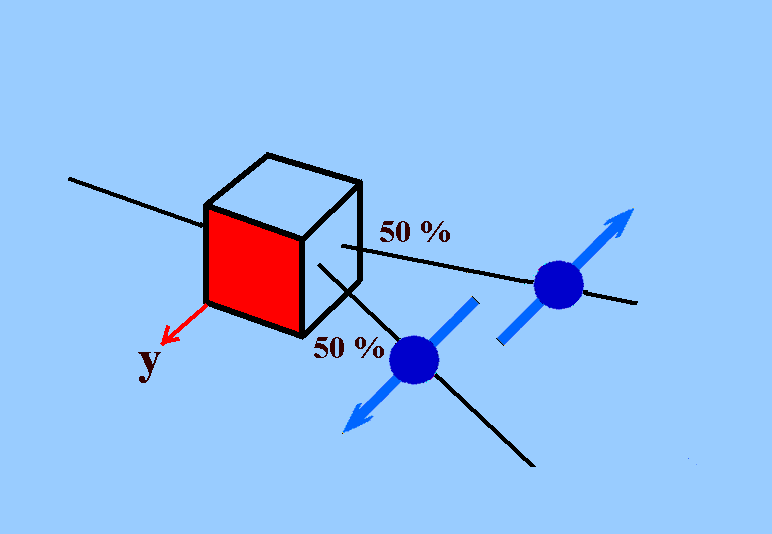
Abb. 1: Spin-Messer mit Bezugsrichtung z (z.B. Magnetfeld). Bei sehr vielen unpolarisiert eintretenden Elektronen sind die austretenden Spins zu jeweils 50% in oder gegen die Bezugsrichtung orientiert. Welches Elektron welchen Spin zeigt, ist zufällig.	Abb. 2: dito mit dem Unterschied: Bezugsrichtung y

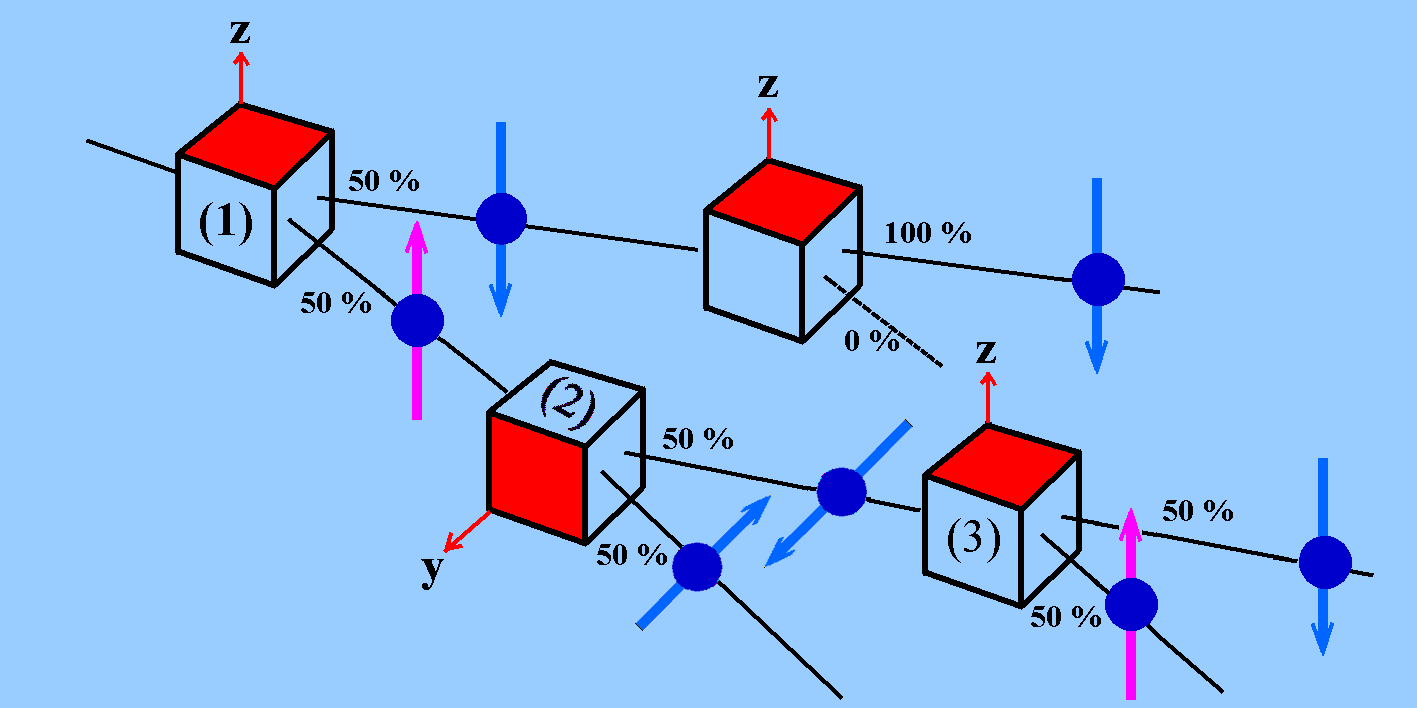Abb. 3: Untere Zeile: Wirkung unterschiedlich orientierter Spin-Messer. Sie demonstriert auch, dass Spin-Messungen bzgl. unterschiedlicher Orientierungen des Spin-Messers komplementär sind: Nach der 2. Messung ist das 1. Messergebnis "vergessen", wie es das Ergebnis nach der 3. Messung bestätigt .

Der Spin-Messer (1) erzeugt aus einem Elektronenstrahl zwei räumlich getrennte Strahlen mit be-stimmten (entgegengesetzten) Spinorientierungen.  Obere Zeile: Misst man ein zweites Mal bei gleicher Bezugsrichtung treten im Idealfall alle eintretenden Elektronen aus. Die blaue Spinorientierung wird so bestätigt. Die Messung durch den 1. Spin-Messer ist reproduzierbar.

Ein Spin-Messer entspricht einem Polarisator für Photonen bzw. Licht mit dem Unterschied, dass ein Spin-Messer zwei räumlich getrennte Ausgänge mit Elektronen mit entgegengesetztem Spin hat, die beide im Prinzip nutzbar sind. Deswegen verwendet wir in den folgenden Zeichnungen, wo nur ein Ausgang genutzt wird, statt eines Spin-Messers das Symbol eines Polarisators.

In den folgenden Zeichnungen sind "aktive" Spin-Messer farbig gekennzeichnet.

© Horst Hübel, Würzburg 2015. Die Darstellung orientiert sich grob am Buch J.J. Sakurai, Modern Quantum Mechanics.

Abb. 4: Der registrierte Durchtritt durch einen Spin-Messer PO stellt eine Messung dar. Da­nach hat das passierende Elektron die be-stimmte Eigen­schaft „polarisiert bzgl. der Richtung PO“. Woher weiß man das? Ein Analysator AN zeigt es. Siehe Abb. 5!	Abb. 5: Alle Elektronen mit be-stimmter Polarisation bzgl. PO treten durch einen parallel ausgerichteten Analysator AN hindurch, keine durch einen dazu senkrechten. Die Elektronen haben also nach Verlassen von PO be-stimmte Polari­sation bzgl. PO als Eigenschaft. Die Messung durch PO ist reproduzierbar.	Abb. 6: Bei schräggestelltem AN haben aus PO austreten­de Elektronen vor AN zwar be-stimmte Polarisation bzgl. PO, aber un-be-stimmte Polarisation bzgl. AN, erkennbar daran, dass bei beliebiger Schrägstellung nicht alle Elektronen AN passieren können. Einige Elektronen treten objektiv zufällig durch AN mit objektiven Wahrscheinlichkeiten. "Objektiv" heißt dabei, dass auf keine Weise festgestellt werden kann, weshalb ein Elektron durchtritt und ein anderes nicht. Von "subjektivem" Zufall würde man sprechen, wenn man den Grund prinzipiell feststellen könnte, aber es nicht getan hat.	Abb. 7: Der Durchtritt eines Elektron durch den Analysator mit der Richtung AN stellt wieder eine Messung der Pola­risation dar. Nach dem Durchtritt durch AN besitzt das Elektron mit Sicher­heit die be-stimmte Eigenschaft „polarisiert bzgl. AN“. Ein zu AN gleich gerichteter Polarisator T („Tester“) be­stätigt das, auch ein zu AN senkrecht orientierter.
Abb. 8: Aus einem Versuchsergebnis (Durchtritt eines Elektrons durch AN) lässt sich nicht auf eine Eigenschaft vor der Messung (durch AN) schließen: Bei fast allen Orientierungen von PO treten durch AN (und T) Elektronen durch.	Abb. 9: Die Eigenschaften „polarisiert bzgl. PO“ und „po­larisiert bzgl. AN“ können nicht gleichzeitig be-stimmt sein. Sie sind komplementär zueinander.	Abb. 10: PO ⊥ T: Nach Durchtritt durch AN haben die Elektronen die frühere Polarisation bzgl. PO „vergessen“. Sonst würden keine Elektronen durch T hin­durch treten.	Abb. 11: erläutert dabei die Wirkung von AN in Abb. 10 als „Quantenradierer“, der frühere Informationen (PO) aus­löscht (PO ⊥ T).

Download PDF-Datei

Elektronenzwillinge verhalten sich anders als zwei klassische Teilchen. Betrachten Sie einen Elektronenzwilling mit Gesamtimpuls und Gesamtspin 0. Mit Hilfe von Lichtschranken und Spin-Messers kann die Frage nach Eigenschaften der einzelnen beitragenden Elektronen gestellt werden: Dann zerfällt der Zwilling in zwei Einzelelektronen mit zum Teil zufälligen Eigenschaften (also unter zufälligen Richtungen und mit zufälligen Spins), die aber die Eigenschaften des Gesamtzustands einhalten (jeweils entgegengesetzt). Misst der Spin-Messer A z.B. zufällig einen Spin ½·h, dann muss der Spin-Messer B den Spin -½·h liefern, damit der Gesamtspin 0 erhalten bleibt, und umgekehrt. Das gilt unabhängig davon, wie weit die beiden Spin-Messer voneinander entfernt sind, im Prinzip sogar bis an den Rand unseres Weltalls, soweit, dass kein Informationsaustausch zwischen den beiden Spin-Messern möglich ist. Es kann sich nicht um eine "Fernwirkung" handeln, auch keine "spukhafte", wie Einstein noch vorgeschlagen hatte. Diese Eigenschaft verschränkter Systeme wird oft auch "Fernwirkungslosigkeit" genannt. All das, weil im verschränkten Zustand des Elektronenzwillings keine zwei einzelnen Elektronen vorhanden sind, sondern erst bei einer Messung mit teils zufälligen Eigenschaften entstehen. Ähnliches gilt für die Impulse, die bei der Messung mit zufälligen Richtungen entstehen, aber so, dass der Gesamtimpuls, z.B. 0 kg·m/s, erhalten bleibt.

E	Bereits bei diesem einfachen Experiment sind einige Grundfakten der Quantenphysik erkennbar.

¹⁾ ideale Spin-Messer vorausgesetzt;

²⁾ Mit freien Elektronen konnte der Stern-Gerlach-Versuch wegen der Lorentz-Kraft auf geladene bewegte Teilchen nicht gelingen. Stern und Gerlach verwendeten stattdessen Ag-Atome, die nach außen elektrisch neutral sind, aber insgesamt den Spin des einzigen Außenelektrons tragen. Vereinfachend wird in diesem Text so getan, als gelänge der Versuch auch mit freien Elektronen und idealisierten Spin-Messern.

³⁾ Genauer müsste man sagen, dass die Spinkomponenten in Bezugsrichtung nur die zwei Werte + ½·h/2π = + ½·ℏ oder -½·h/2π = - ½·ℏ  haben kann.

⁴⁾ Um das einzusehen, braucht man nicht auf halbklassische Modelle wie das "Heisenberg-Mikroskop" zurückgreifen. Mit diesem Modell wird manchmal die Komplementarität von Ort und Impuls/Geschwindigkeit eines Elektrons (bzw. die Heisenberg'sche Un-bestimmtheits-Relation) durch mechanische Stöße bei der Beleuchtung mit Photonen plausibel gemacht.

⁵⁾ Man hat versucht, den Elektronenspin durch eine "Eigendrehung" des Elektrons zu erklären, ähnlich der Eigendrehung eines Tennisballs. Aber was soll eine Drehung eines punktförmigen Gegenstands wie eines Elektrons sein?

⁶⁾ Kann man die Polarisation oder den Spin eines einzelnen Quantenteilchens überhaupt messen?

⁷⁾  Ein alternativer Zugang zu Un-bestimmtheit und Be-stimmtheit liegt dem Konzept des Welle-Teilchen-Dualismus zugrunde. Leider hat dieser historisch zu vielen Interpretations-Missverständnissen, vor allem in schulischen und populärwissenschaftlichen Texten geführt.

Vgl.: Veranschaulichung von Grundfakten der QM mit polarisiertem Licht

          G47c Einige Grundfakten von Quantenobjekten