Grundlage ist das Kausalkettenschema zur Berechnung von Bewegungen.

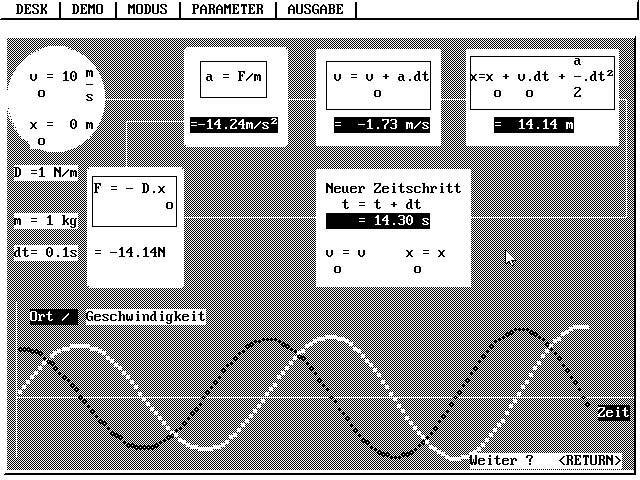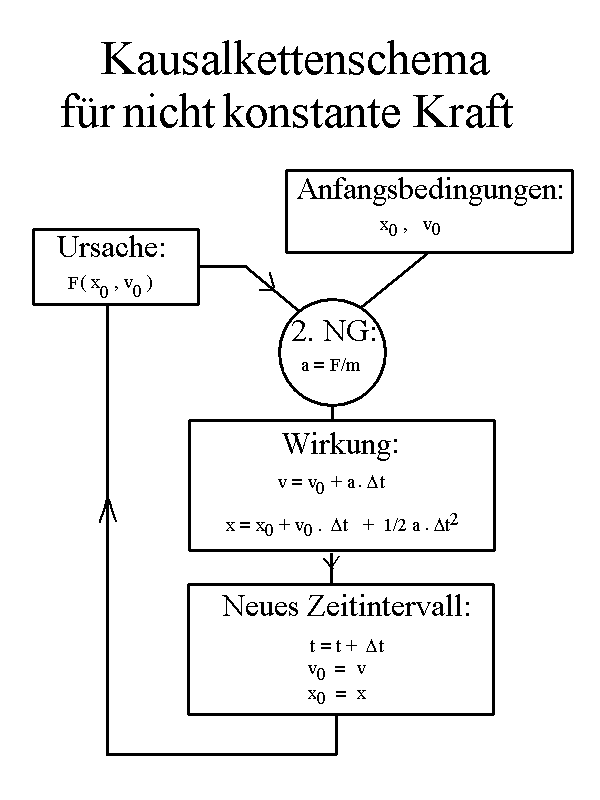
Wenn die Kraft F im Laufe der Bewegung nicht konstant ist, hilft folgende Überlegung: Wähle einen Zeitabschnitt Δt (ein Zeitintervall Δt), so dass in ihm F und a weitgehend konstant sind. Dann kannst du das Kausalkettenschema für konstante Kraft anwenden. Für das nächste Zeitintervall berücksichtigst du nun die veränderte Kraft. Also du startest einen neuen Zeitabschnitt, indem du die zuvor erreichte Geschwindigkeit als neue Anfangsgeschwindigkeit wählst, den zuvor erreichten Ort als neuen Anfangsort, möglicherweise ergibt sich aus beiden die für das neue Zeitintervall zuständige Kraft du durchläufst jetzt die "Kausalschleife" für das neue Zeitintervall, usw. Wenn du das für eine bestimmte Breite Δt des Zeitintervalls durchgeführt hast, und es stellt sich heraus, dass die so berechnete Bewegung mit der Beobachtung übereinstimmt, solltest du Δt verkleinern. In vielen Fällen kannst du dann die Übereinstimmung verbessern. Die Anfangsbedingungen können niemals exakt angegeben werden. In vielen Fällen wirken sich aber kleine Messfehler in den Anfangsbedingungen auch nur wenig auf das Rechenergebnis aus. Es gibt aber auch Kräfte, für die geringste Abweichungen in den Anfangsbedingungen verheerende Abweichungen für die berechneten x und v-Werte haben (Chaostheorie; deterministisches Chaos).

Durch das PC-Programm KAUSALIT mit der Methode kleiner Schritte berechnete harmonische Schwingung. Das Programm zeigt auf dem Bildschirm alle Rechenschritte für beliebige Parameter und die t-x- und t-v-Graphen. Für die ersten 2 oder 3 Schritte könntest du das Kausalkettenschema auch per Hand vollziehen. Für den gewählten Zeitschritt Δt = 0,1 s (im Vergleich zur Schwingungsdauer T = 6,3 s ) ergibt sich ein relativ geringes - durch die Näherungen des Verfahrens bedingtes - Anwachsen der Amplitude. Für kleineres Δt könnte der Fehler verringert werden.

Hinweis: Das hier geschilderte Verfahren entspricht in etwa dem so genannten Halbschrittverfahren. Das so genannte Euler'sche Verfahren ist für Handrechnungen etwas einfacher, leider auch ungenauer. Hier wird für die Schule die oben erläuterte Methode vorgeschlagen. Dem Computer ist nämlich gleichgültig, ob er eine etwas einfachere oder kompliziertere Rechenformel bearbeiten soll. Zudem sind die hier verwendeten Rechenformeln die in der Mechanik zu verwendenden Standardformeln, mit denen du dich schon länger beschäftigt hast.

Befürworter des Euler'schen Verfahren im Unterricht komplizieren m.E. den Sachverhalt manchmal, indem sie erst eine (unzureichende) Bewegungslehre mit nur einer Anfangsbedingung entwickeln, dann für die Methode kleiner Schritte auch die zweite Anfangsbedingung ins Spiel bringen, dann aber die Formeln der Bewegungslehre ohne den quadratischen Term in einer Weise vereinfachen, die sie vorher den Schülern gerne ausgeredet hätten. Das Problem der reduzierten Genauigkeit bewältigen sie mit stark verringertem Δt. Mit der Euler'schen Methode kann man nicht einmal einen freien Fall exakt bewältigen! Dafür ist die hier vorgeschlagene Methode exakt (aber evtl. unnötig aufwändig).

.

( September 2013 )