|
SG144 Beispiel zur Delta-Methode: t-x- und t-v-Funktion ©
H. Hübel Würzburg 2013
|
Impres-sum |
.
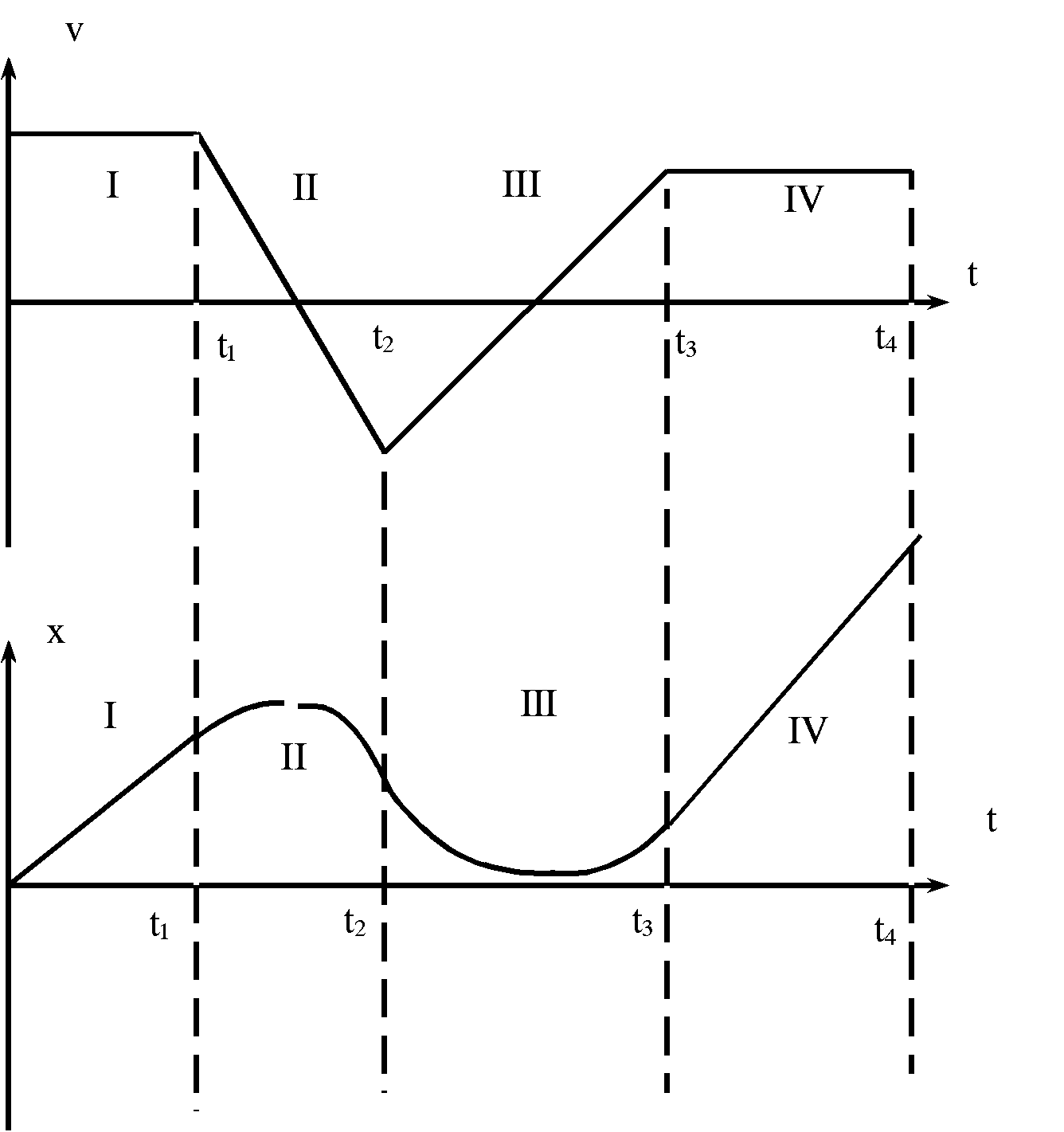
| Stellen Sie, ausgehend von den Grundgleichungen für die gleichmäßig beschleunigte Bewegung, das t-x-Gesetz und das t-v-Gesetz für die durch die Graphik gegebene Situation dar! |
.
|
Grundgleichungen |
|
| a = konst. | . |
| v = v0 + Δv | Δv = a · Δt |
| x = x0 + Δx | Δx = v0 · Δt + ½ · a · Δt2 |
Dabei sind x0 und v0 Anfangsort und Anfangsgeschwindigkeit zu Beginn des jeweiligen Intervalls Δt.
Ziel ist es, Lösungsverfahren einzusetzen, die weder viel "Wissen" voraussetzen, noch eine Formelsammlung. Statt in irgendwelche "Formeln" einzusetzen, bietet es sich in diesem Sinn an, immer von (den wenigen) Grundgleichungen oder allgemeinen Lösungsverfahren auszugehen.(Vgl. "Strategien statt Formeln!")

| Lösen Sie niemals eine Aufgabe ohne Graphen! |
In den einzelnen Bereichen gilt:
(I) v = v0
x = v0 · t
(II) v = v0 + a1 · (t - t1 ) wobei a1 < 0
x = x1 + v0·(t - t1 ) + ½·a1·(t - t1 )2
also Δt = t - t1 (das Zeitintervall II beginnt zum Zeitpunkt t1)
(III) v = v2 + a2 · ( t - t2 ) wobei a2 >0
x = x2 + v2·(t - t2 ) + ½·a2·(t - t2 ) 2 also Δt = t - t2 (das Zeitintervall III beginnt zum Zeitpunkt t2)
(IV) v = v3 = konst.
x = x3 + v3·(t - t3 ) also Δt = t - t3 (das Zeitintervall IV beginnt zum Zeitpunkt t3)
Die konstanten Anfangsbedingungen für jedes Intervall ergeben sich aus dem am Ende des Vorgängerintervalls erreichten Werten, also z.B. x1 = v0· t1 , x2 = x1 + v0·(t2 - t1 ) + ½·a1·(t2- t1 )2 = v0·t2 + ½·a1·(t2- t1 )2 .
Im Unterricht wird man eine ähnliche Aufgabe durchrechnen, vielleicht mit konkreten Werten für die einzelnen Zeiten und Anfangswerte.
Sie sollen einsehen, dass man nichts als die Grundgleichungen im Kasten oben braucht: kein unnötiges Formellernen!
.
.
.