Hier wird nur die stationäre erzwungene Schwingung nach Beendigung des Einschwingvorgangs betrachtet.

Bei einer erzwungenen Schwingung schwingt das Pendel immer mit der Erregerfrequenz f (manchmal auch f_err genannt). Aber die Amplitude A hängt davon ab, wie gut die Erregerfrequenz f mit der Eigenfrequenz f₀ übereinstimmt.

Ein Versuch soll die Abhängigkeit der Amplitude von der Erregerfrequenz f klären:

Ein hängendes Federpendel (schwingende Masse m, Federhärte D) wird mittels eines Exzenters zu erzwungenen Schwingungen angeregt. Gemäß des Verfahrens der "Aufhängungskopplung" wird durch den Exzenter der Aufhängepunkt der Feder mit der Erregerfrequenz auf und ab bewegt. Die Schwingung des Aufhängepunkts soll die Amplitude H haben, die in Schulbüchern oft "Hub" H heißt.

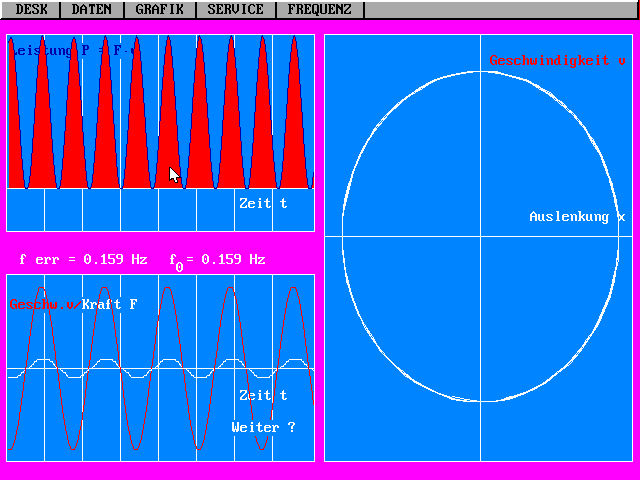Stationäre erzwungene Schwingung, wenn die Erregerfrequenz mit der Eigenfrequenz übereinstimmt. Dargestellt sind hier Geschwindigkeit v und Kraft F, mit der der Erreger an der Aufhängung zieht (unten links). Das Produkt beider ist die Leistung (Energie pro s; oben links dargestellt), die vom Erreger an das Pendel übertragen wird (rot), oder die vom Pendel an den Erreger zurückgegeben wird (grün; hier aber nicht vorhanden). Rechts ist gezeigt, wie sich Geschwindigkeit v und Auslenkung x im Laufe einer Periode verändern. Dem Pendel wird offenbar ständig Energie zugeführt (oben links: nur rot). Kraft und Geschwindigkeit sind in Phase. Die Amplitude hat ihren konstanten, sogar maximalen Wert erreicht (stationäre Schwingung).

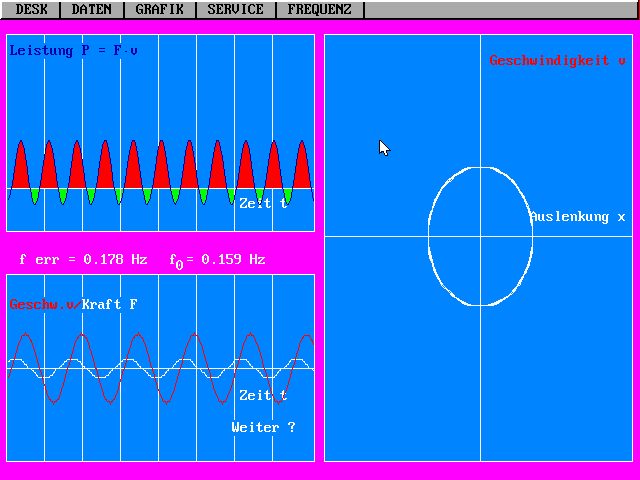Stationäre erzwungene Schwingung, wenn die Erregerfrequenz die Eigenfrequenz überschreitet. Kraft und Geschwindigkeit sind so phasenverschoben, dass ein Teil der pro Periode zugeführte Energie wieder an den Erreger zurückgegeben wird (grün): relativ kleine Amplitude.

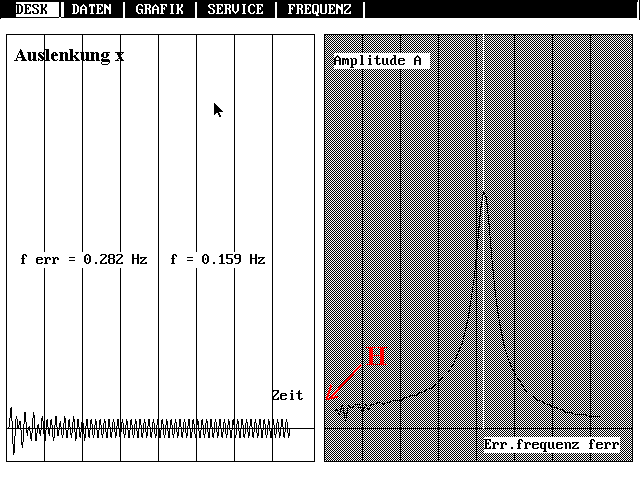Resonanzkurve für den Fall der so genannten "Aufhängungskopplung". Geteilter Bildschirm einer Simulation der Resonanz mit dem Programm LEISTRES.exe. Die Schwingung wird simuliert (links). Wenn der Einschwingvorgang abgeschlossen ist, wenn also eine stationäre Amplitude A erreicht ist, wird in das Diagramm rechts ein Punkt (ferr,A) eingetragen. Dann wird die Frequenz geändert. Für ferr => 0 strebt die Amplitude A gerade gegen den Hub H.

Der genaue Verlauf der Resonanzkurve, besonders auffällig bei sehr kleinen und sehr großen Frequenzen, hängt von der Art der Kopplung zwischen Erreger- und erzwungener Schwingung ab. Bei Frequenzen nahe der Eigenfrequenz ("Resonanzfrequenz") verhalten sich alle Resonanzkurven unabhängig von der Kopplung weitgehend gleich.

Bei einer bestimmten Art der Kopplung ("Aufhängungskopplung") zwischen Erreger und Pendel folgt das Pendel bei kleinen Frequenzen der Erregerschwingung trägheitslos (A ≈ H). Bei sehr hohen Frequenzen f kommt das Pendel immer weniger mit: mit wachsender Frequenz strebt die Amplitude A gegen 0. Dazwischen gibt es eine Frequenz, bei der die Amplitude maximal und u.U. extrem groß wird. Das ist der Fall, wenn die Erregerfrequenz f ungefähr mit der Eigenfrequenz f₀ übereinstimmt. (Man kann die Frequenz f genau angeben. Wir interessieren uns hier aber nicht für die exakte Gesetzmäßigkeit.). Das Amplitudenmaximum ist umso höher, je geringer die Dämpfung ist.

Energetisch lässt sich das leicht verstehen: Bei kleinen Frequenzen wird die Kopplungsfeder kaum  beansprucht; sie überträgt kaum Energie; das Pendel schwingt mit kleiner Amplitude. Wenn die beiden Frequenzen ungefähr übereinstimmen, ist die Phasenverschiebung zwischen Erreger- und Pendelschwingung gerade so, dass fast zu jedem Zeitpunkt einer Periode Energie vom Erreger auf das Pendel übertragen wird: die Amplitude A wächst und wächst, wobei auch die Energieverluste durch Reibung ansteigen. Das Amplitudenmaximum ist erreicht, wenn in einer Periode gerade soviel Energie durch Reibung verloren geht, wie durch den Erreger zugeführt wird. Bei sehr hohen Frequenzen ist die Phasenverschiebung zwischen Erreger und Pendel gerade so, dass die in einer Halbperiode zugeführte Energie in der nächsten Halbperiode an den Erreger zurückgegeben wird. Das Pendel nimmt insgesamt keine Energie auf und behält seine kleine Amplitude bei.

Diese Erscheinung einer u.U. riesigen Amplitude A bei (ungefährer) Übereinstimmung der beiden Frequenzen heißt Resonanz. Resonanz ist manchmal erwünscht (z.B. wird die Tonhöhe vieler Musikinstrumente so bestimmt), manchmal extrem schädlich (Resonanzkatastrophe, z.B. bei einer Brücke).

Die Erscheinung der Resonanz selbst, wenn die Erregerfrequenz ungefähr mit der Eigenfrequenz übereinstimmt, ist unabhängig von der Art der Kopplung.

Mehr zur Resonanz bei mechanischen Pendeln ist hier zu finden.

( September 2013 )