. Startseite FORPHYS .

Physik für Schülerinnen und Schüler Druck © H. Hübel Würzburg 2013

Empfohlene Glossarthemen: Druck Dichte Temperatur

Glossar Physik für Schülerinnen und Schüler

Impres-sum

1. Druck als Spannungszustand - "Kraft macht Druck"

Wenn du einen Luftballon aufbläst, merkst du schnell, dass in der eingeschlossenen Luft ein "Spannungszustand" entsteht. Je mehr Luft du hinein geblasen hast, desto schwieriger wird es, noch mehr Luft hinein zu pumpen. Du könntest richtig vermuten, dass auch die sich immer stärker dehnende Gummihaut eine Rolle spielt. Aber auch, wenn du einen Fahrradschlauch aufpumpst, bemerkst du, dass es immer schwerer geht, ohne dass sich der Schlauch im Reifen wesentlich mehr ausdehnt.

Nimmst du einen aufgeblasenen Luftballon und presst ihn mit äußeren Kräften zusammen, so erhöht sich in der eingeschlossenen Luft eine Art "Spannung", erkennbar daran, dass es immer schwerer wird, ihn weiter zusammen zu pressen, oder dass Teile des Luftballons "ausweichen". Bei extrem starken äußeren Kräften kann der Spannungszustand in der eingeschlossenen Luft sogar dazu führen, dass der Luftballon platzt.

Genauso entsteht ein Spannungszustand im eingeschlossenen Gas oder einer eingeschlossenen Flüssigkeit in einer Spritze, wenn du bei geschlossener Austrittsöffnung auf den Stempel drückst. Häufig nennt man das zylindrische Gefäß der Spritze Zylinder; der Stempel heißt oft auch Kolben, besonders beim PKW sind Zylinder und Kolben die Grundlage für die Funktion des Motors und von Bremsen.

Der Spannungszustand in einer Flüssigkeit oder einem Gas wird Druck p genannt.

Wir haben also kennengelernt:

und meinen damit die Kraft auf den Kolben/Stempel bei einem Zylinder und den Spannungszustand in dem eingeschlossenen Gas oder der Flüssigkeit.

Wir suchen jetzt ein Maß für den Spannungszustand/Druck. Es ist plausibel, dass der Spannungszustand/Druck umso größer sein wird, je größer die Kraft auf den Kolben/Stempel ist. Du weißt auch: Stöckelschuhe mit Pfennigabsätzen hinterlassen in Asphalt tiefe Spuren, während selbst bei größerer Masse Personen mit größeren, flachen Absätzen keine Spuren hinterlassen. Traktoren und Geländewagen haben Räder mit einem größeren Radius als PKWs, damit die Auflagefläche größer ist. Sie sinken dann nicht so leicht in lockeres Erdreich oder Sand ein. Es ist also plausibel, dass der Druck umso größer ist, je kleiner die Fläche ist, auf die die Kraft wirkt, also hier, je kleiner die Querschnittsfläche des Stempels ist.

Versuchsweise wird also definiert: Ein Maß für den Spannungszustand/Druck soll

sein, wobei F der Betrag einer Kraft F ist, die senkrecht auf einen Stempel mit der Querschnittsfläche A wirkt, also p = /F/ / A . Beachte: Der Druck p ist nicht "Kraft pro Fläche", wie manchmal behauptet wird, denn die Kraft ist ja ein Vektor, und in die Druckformel geht nur der Betrag der Kraft ein. Deshalb hat der Druck auch keine Richtung wie eine Kraft. Der Druck p kennzeichnet nur den Spannungszustand, der in dem Gas oder der Flüssigkeit herrscht.

[p] = 1 N/m² = 1 Pa

Es sind verschiedene Einheiten für den Druck üblich: Zunächst ergibt sich aus der Definitionsgleichung [p] = 1 N/m² . Dafür wird zur Abkürzung auch Pa (Pascal) verwendet nach einem berühmten französischen Physiker, Mathematiker, Theologen und Philosophen des 17. Jahrhunderts, der bahnbrechende Entdeckungen im Zusammenhang mit dem Druck gemacht hat. Es gilt also:

Ein Druck p = 1000 HPa = 100 000 N/m² = 10 N/cm² bedeutet, dass senkrecht auf 1 m² Fläche eine Kraft von 100 000 N wirkt bzw. auf 1 cm² die Kraft von 10 N.

Hinweis: 1 m² = 100 dm² = 10 000 cm² ("Die Umrechnungszahl bei Flächenmaßen ist 100!").

1 Pa ist eine sehr kleine Druckeinheit. Ein solcher Druck entsteht ja schon, wenn eine Kraft von 1 N auf einen Stempel mit der Querschnittsfläche 1 m² wirkt. Der Luftdruck auf der Erdoberfläche schwankt, aber ist immer ca. 1000 HPa = 1000·100 Pa = 100 000 N/m² (HPa = Hektopascal). Deshalb war früher eine andere Druckeinheit in Gebrauch, die man auch heute noch manchmal liest, z.B. auf dem Reifendruckmesser:

1 bar = 1000 HPa.

Dieser Druck entspricht etwa dem Luftdruck auf Meereshöhe.

Ärzte messen den Blutdruck in den Arterien immer noch mit der Einheit 1 Torr = "1 mm Quecksilbersäule". Für die Umrechnung gilt: 760 Torr = 1000 HPa.

Warum aus historischen Gründen solche seltsamen Maße verwendet werden, wirst Du in Kürze kennen lernen.

Musteraufgabe 1: Auf den Kolben eines Bremszylinders einer Bremse wird mit dem Fuß eine Kraft von 20 N ausgeübt. Die Querschnittsfläche des Kolbens beträgt 2 cm2. Welcher Druck entsteht in der eingeschlossenen Bremsflüssigkeit? Gegeben: F = 20 N, A = 1 cm2 = 1/100 dm2= 1/10000 m2 ("Die Umrechnungszahl bei Flächenmaßen ist 100"). Gesucht: p p = F/A = 20 N / (1/10000 ) m2 = 200 000 N/m2 = 2000 HPa ( = 2 bar )

In den Zylindern einer hydraulischen Anlage (zum Bewegen einer Baggerschaufel etwa oder bei einer Hebebühne für Kraftfahrzeuge) sind Drucke bis 400 bar = 40 000 000 Pa = 40 MPa durchaus technisch möglich.

2. "Druck macht Kraft"

Wozu braucht man überhaupt in einem PKW soviele Zylinder mit Kolben? In der Regel hat ein Motor 4 Zylinder. Zu jedem Rad gehört ein Bremszylinder. Citroen regelte früher in bestimmten Autotypen auch die Federung oder das Höherstellen bei unwegsamem Gelände hydraulisch mit Zylindern und Kolben. Auch bei Servolenkungen werden die Lenkbewegungen der Fahrer durch Zylinder mit Kolben erleichtert. Grund ist, dass man mit Druck Kraft erzeugen kann.

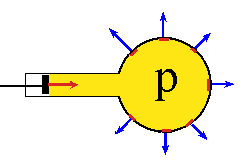
Beim Luftballon ist dir das klar. Wenn sich die Luft in seinem Inneren erwärmt, z.B. durch Sonnenstrahlung, steigt auch der Druck an. Dann entsteht auf jedes Flächenstück der Innenwand eine vergrößerte senkrechte Kraft. Sie ist es, die den Luftballon weiter aufbläht. Wetterballons, die in Höhen von einigen km steigen können um dort Temperatur und Windgeschwindigkeit zu messen, kann sie manchmal sogar zum Platzen bringen.

Abb. 1:  Auf jedes Flächenstück (rot) entsteht eine Kraft (blau) senkrecht dazu.

Verbindet man zwei Zylinder mit Kolben unterschiedlicher Querschnittsfläche miteinander, so entsteht eine hydraulische Presse (Abb. 2). Zwei luft- oder wassergefüllte Spritzen, deren Öffnungen mit einem Schlauch verbunden sind, sind ein Modell dafür. Übt man auf einen Kolben 1 eine Kraft F₁ parallel zur Achse des Zylinders aus, entsteht zuerst ein Druck p = F₁/A₁ im Inneren beider Kolben (also ein Spannungszustand). Durch p entsteht am zweiten Zylinder eine Kraft F₂ senkrecht zu dessen Querschnittsfläche A₂. Sie kann den zweiten Kolben verschieben.

Messungen zeigen: Man erhält genau die Kraft F₂ = p·A₂ = F₁/A₁·A₂, wenn man annimmt, dass der Druck p überall in den beiden verbundenen Zylindern gleich ist. Als Ergebnis merken wir uns:

1. Durch einen Druck p entsteht an jeder Fläche A, die dem Druck ausgesetzt ist, eine Kraft senkrecht zu dieser Fläche mit dem Betrag F = /F/ = p·A ("Druck macht Kraft"). 2. In miteinander verbundenen Gefäßen (Zylindern), die mit Gas oder Flüssigkeit gefüllt sind, herrscht überall der gleiche Druck.

3. Die Hydraulische Presse

Bei einer Hebebühne in einer Kfz-Werkstatt nutzt man genau dieses um mit einer kleinen Kraft eine große Kraft auszuüben, mit der sogar ein PKW angehoben werden kann.

1. Mit einer kleinen Kraft F₁ soll ein großer Druck erzeugt werden. Man braucht dazu einen Kolben mit kleiner Querschnittsfläche A₁. Es entsteht der Druck p = F₁/A₁ ("Kraft macht Druck").
2. Der Druck ist überall gleich, also auch im Zylinder mit einer großen Querschnittsfläche A₂.
3. Senkrecht zu dessen Kolbenquerschnitt A₂ entsteht eine Kraft F₂ = p·A₂ ("Druck macht Kraft"). Wenn A₂ >> A₁ ist dann auch F₂ >> F₁. Aus einer kleinen Kraft F₁ entsteht eine große Kraft F₂!
   

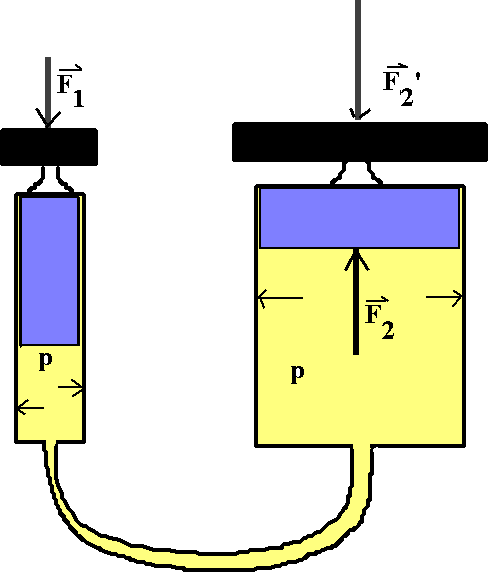Abb. 2: Modell einer hydraulischen Presse Überall im Inneren herrscht der gleiche Druck (= Spannungszustand) p. Wir sagen: In dem einen Kolben gilt "Kraft macht Druck" (die von außen ausgeübte Kraft F1 nämlich). In dem anderen Kolben gilt "Druck macht Kraft", nämlich die entstehende Kraft F2. Mit einer Gegenkraft  F2' zu F2 entsteht häufig Kräftegleichgewicht. Dann werden die Kolben nicht weiter verschoben.

Es gibt hydraulische Pressen, mit denen man in der Werft den ganzen Rumpf eines Ozeanriesen anheben, oder Teile davon zusammenpressen kann, damit sie zusammengeschweißt werden können.

Natürlich erinnerst du dich an die Goldene Regel: Mit einer einfachen Maschine (wie der hydraulischen Presse) kann zwar Kraft "gespart" werden (F₁ < F₂), aber keine Arbeit W. Deswegen muss zur größeren Kraft F₂ ein kürzerer Kraftweg s₂ gehören, damit das Produkt W = F₁·s₁ = F₂·s₂ konstant bleibt. Du siehst das auch mit dem Spritzenmodell: Obwohl sich der Kolben/Stempel mit der kleineren Querschnittsfläche A₁ beträchtlich verschiebt (s₁ groß), verschiebt sich der Kolben/Stempel mit der größeren Querschnittsfläche A₂ kaum (s₂ klein). Entsprechendes gilt umgekehrt.

So kann man die Verhältnisse bei der Hydraulischen Presse auf 3 verschiedene Weisen erklären:

1. mit Hilfe des Drucks (wie oben: Spannungszustand überall gleich),
2. mit Hilfe der Goldenen Regel (große Kraft <=> kleine Verschiebung),
3. mit der Volumenerhaltung der eingeschlossenen Flüssigkeit: Das Volumen, das in einem Kolben verdrängt wird, verdrängt im anderen Kolben den Stempel.

Es ist nämlich so, dass das ganze Flüssigkeitsvolumen V = A₁·s₁, das aus dem Zylinder 1 mit dem Stempel herausgedrückt wird, im Zylinder 2 wieder auftreten muss, wenn die Flüssigkeit nicht zusammengedrückt werden kann ("inkompressible Flüssigkeit"). Es gilt dann also auch V = A₂·s₂. Damit die beiden Produkte gleichen Wert haben, muss zur größeren Querschnittsfläche A₂ die kleinere Verschiebung s₂ gehören, und wegen der Goldenen Regel zu dieser die größere Kraft.

Beim Automotor wird in jedem der Zylinder ein Benzin-Luft-Gemisch durch einen Zündfunken zur Verbrennung gebracht. Dabei steigt der Druck im Zylinder stark an und übt Kräfte auf die Wandung und den Kolben aus. Nur dieser kann nachgeben. Er verschiebt sich mit großer Kraft. Mit Hilfe der Kurbelwelle wird die lineare Bewegung des Kolbens in eine Rotationsbewegung umgesetzt, die den PKW antreibt. Mehrere Zylinder (meistens 4) werden eingesetzt um die Laufruhe des Motors zu erhöhen. Denn nach der Verbrennung muss der Kolben "zurückgeholt" werden. In dieser Zeit kann bestenfalls keine Kraft auf die Kurbelwelle übertragen werden; der PKW würde sogar kurzzeitig langsamer werden. Indem das Benzin-Luft-Gemisch in einem der Zylinder nach dem anderen im richtigen Zeitabstand gezündet wird, werden die "Toten Punkte" durch die Nachbarzylinder überwunden; es wirkt quasi ständig eine Antriebskraft auf die Kurbelwelle:

Musteraufgabe: In einer Hebebühne für Kraftfahrzeuge wird auf einen Kolben 1 mit der Querschnittsflä­che A1 = 2 cm2; eine Kraft F1 = 20 N ausgeübt. Dadurch entsteht am Kolben 2 eine Kraft F2 von 3000 N. Welche Querschnittsfläche A2 muss der Kolben 2 haben? Um welche Strecke s1 verschiebt sich der Kolben 1, wenn das Fahrzeug mittels Kolben 2 um s2 = 5 cm = 0,05 m gehoben wird? Wie könnte das technisch realisiert werden? Geg.: F1 = 20 N, F2 = 3000 N ; A1 = 2 cm2 = 0,02 dm2 = 0,0002 m2; s2 = 0,05 m Ges.: p, A2, s1 Lösung: p = F1/A1 = 20 N/0,0002 m2 = 1·105 N/m2 Wegen p = F2/A2 folgt A2 = F2/p = 500 N/(1·105 N/m2) = 500·10-5 N·m2/N = 5·10-3 m2 = 50·10-4 m2 = 50 cm2 . Dazu gehört ein Radius von ca. 4 cm. Wegen V = A1·s1 = A2·s2 folgt s1 = A2·s2/A1 = 50 cm2/2cm2· 5cm = 125 cm = 1,25 m. So lange Zylinder wären sehr unhandlich. Deshalb verwendet man einen kurzen Zylinder 1, presst aber den Kolben 1 mehrmals in ihn hinein (so dass nach und nach die 1,25 m zustande kommen). Durch Ventile muss man dann aber dafür sorgen, dass beim "Zurückholen" des Kolbens 1 (vor dem nächsten Pressen) nicht Hydraulik-Flüssigkeit zurückfließt, sondern anschließend sogar von außen zugeführt werden kann.

Eine hydraulische Presse ist neben Seil, Flaschenzug, Schiefe Ebene eine weitere einfache Maschine, mit der keine Arbeit gespart oder gewonnen werden kann. Auch für sie gilt die Goldene Regel.

Hydraulische Pressen dienen auch zum Stanzen von Karosserie- oder auch kleineren Blechteilen, zum Formen von Karosserieteilen bei PKWs, zum Formen von Kunststoffteilen, zum Münzprägen.

4. "Druck macht Kraft" im Teilchenmodell

Abb. 3: Bei Wandstößen werden (zur Wand) senkrechte und parallele Kräfte übertragen. Im zeitlichen Mittel heben sich die parallelen aber gegenseitig auf.

Betrachten wir eine luftgefüllte Spritze. Die Teilchen (Moleküle, Atome) des Gases sind in heftiger Bewegung und stoßen nach einer gewissen Strecke freien Flugs untereinander und mit der Wand zusammen. Du weißt schon, dass sich die Teilchen im Mittel umso schneller bewegen, je höher die Temperatur des Gases ist. Hier brauchen wir aber eine andere Eigenschaft, die mit dem Spannungszustand/Druck verbunden ist: Auch je höher der Druck ist, desto öfter stoßen die Teilchen in der gleichen Zeiteinheit zusammen oder gegen die Wand. Bei jedem Wandstoß üben sie eine Kraft auf die Wand aus, je höher der Druck, umso öfter. Umso größer ist dann auch die mittlere Kraft, die in der Zeiteinheit auf ein Stück der Wand ausgeübt wird. Zum Teil heben sich die bei den Stößen übertragenen Kräfte gegenseitig auf (die Komponenten der Kraft parallel zur Wand). Von zwei Teilchen, die Stöße nach Art der Abb. 3 übertragen, "überleben" nur die Kraft-Komponenten senkrecht zur Wand: Durch den Druck entstehen Kräfte senkrecht zu jedem Flächenstück, das sich dem Druck darbietet.

Würde man zusätzlich noch die Temperatur erhöhen, würden sich die Teilchen im Mittel schneller bewegen, öfter miteinander und gegen die Wand stoßen und noch mehr Kräfte übertragen. Wir würden das als angestiegenen Druck registrieren.

Erhöhte Temperatur: Die Teilchen bewegen sich im Mittel schneller (haben im Mittel höhere kinetische Energie) Erhöhter Druck: Die Teilchen stoßen im Mittel öfter untereinander und gegen die Wand. Sie übertragen deshalb im Mittel eine größere Kraft auf die Wand.

5. Druckmessung

Zum Druckmessen dient ein Manometer oder Barometer. Letzten Endes misst man dabei in der Regel eine Kraft. Das Grundprinzip ist Folgendes: ein spiralförmig ausgebildetes Gefäß wird mit dem druckhaltigen Gefäß verbunden. Schließlich herrscht in beiden Gefäßen der gleiche Druck. Durch den Druck entsteht im  spiralförmigen Gefäß eine Kraft auf die Wandung, durch die die Wand verformt wird. Das ganze Gefäß wird so verformt. Mittels Zahnrädern wird die Verformung auf einen Zeiger übertragen. Der Zeiger schlägt umso mehr aus, je mehr das Gefäß verformt wurde, je größer der Druck ist.

Bei modernen Druckmessern wird ein Halbleiterbauteil durch die entstehenden Druckkräfte verformt. Dabei ändert sich sein elektrischer Widerstand, der gemessen und als Maß für den Druck genommen wird.

Als Drucksensor dient dann direkt dieses Halbleiterbauteil. Man kann aber auch ein abgeschlossenes Gasvolumen ("Sensorgas") nehmen, dessen Druck mit dem Drucksensor gemessen wird. Es ist über eine Membran in Kontakt mit dem Gas oder der Flüssigkeit, in dem der Druck gemessen werden soll. Entstehen durch den zu messenden Druck Kräfte auf die Membran, so ändert sich der Druck im "Sensorgas".

Bisher haben wir immer angenommen, dass der Druck in einem Gefäß allein durch eine äußere Kraft auf den Stempel des Zylinders zustande kommt. Manchmal nennt man dann den Druck auch Stempeldruck. Jetzt wollen wir eine andere Ursache des Drucks untersuchen.

6. Der Schweredruck

Ein hohes Gefäß wird mit Wasser gefüllt. Obwohl kein Stempel vorhanden ist, kann man in unterschiedlicher Tiefe mit einem Drucksensor unterschiedlichen Druck messen. Der Druck ist umso höher, je höher die Wassersäule über dem Drucksensor. Das kennst Du auch aus eigener Erfahrung beim Tauchen. Hier arbeitet dein Ohr als Drucksensor. Je tiefer du tauchst, desto höher ist der Druck auf dein Trommelfell. Du kennst auch den Effekt, dass man beim Fahren auf einen Berg oder von einem Berg von einer gewissen Höhe ab schlechter hört. Beim Abwärtsfahren herrscht im Mittelohr noch der Luftdruck von oben. Der äußere Luftdruck (unten erhöht) drückt dann dein Trommelfell soweit nach innen, dass es Schallschwingungen kaum mehr folgen kann. Beim Steigen ist der innere Druck im Vergleich zum äußeren erhöht (noch von tieferen Positionen her) mit den gleichen Folgen. Durch Schlucken kannst Du leicht zum Druckausgleich zwischen Mittelohr und Gehörgang sorgen und wieder normal hören. Der Effekt ist umso stärker, je größer der Höhenunterschied.

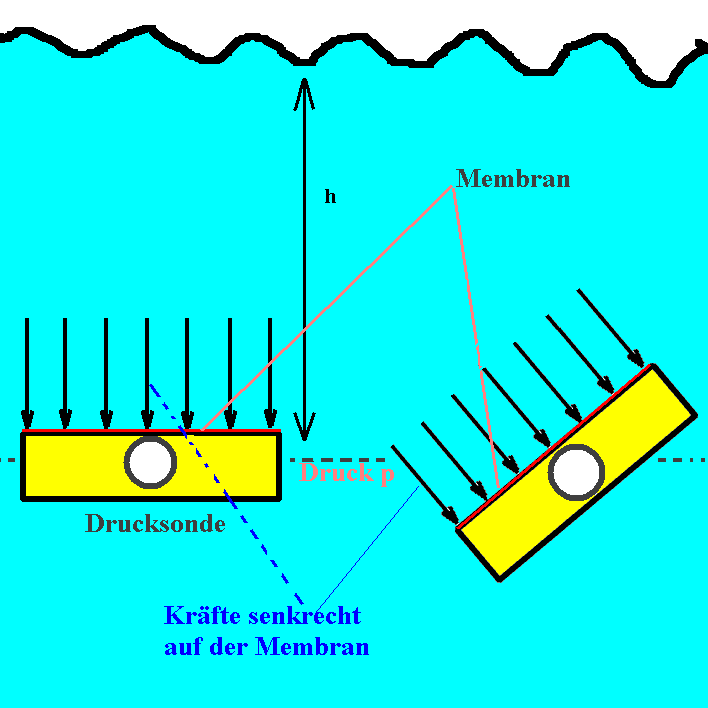Abb. 4: Die Höhe h der Wassersäule über der Sensorfläche (Membran) der Drucksonde bestimmt den Druck. Bei gleichem Druck entstehen senkrecht zur Membran gleich große Kräfte, unabhängig von der Orientierung der Drucksonde.

Messungen zeigen: Der Druck in einer Tiefe h, wenn also die über der Messstelle liegende Flüssigkeits- oder Gassäule h ist, ist proportionale zu dieser Höhe h. Er hängt auch von der Dichte ρ der Flüssigkeit ab (Gleiches gilt für Gase). Es ist deshalb naheliegend, ihn auf die Gewichtskraft auf die über der Sensorfläche A liegenden Flüssigkeitssäule zurückzuführen. Abb. 4 zeigt es: Wenn A die Sensorfläche der waagrechten Drucksonde ist, dann hat bei einer Höhe h der darüber liegenden Flüssigkeitssäule diese das Volumen V = A·h und damit die Masse m = V·ρ = A·h·ρ, wenn die Dichte ρ konstant ist. Die Gewichtskraft auf diese Flüssigkeitssäule hat also den Betrag F_G = m·g = A·h·ρ·g. Dann ergibt sich ein Schweredruck p = F_G/A = ρ·g·h, also

p = ρ·g·h

Genau das zeigt das Experiment; wir haben ein richtiges Modell der Wirklichkeit konstruiert, nämlich Druck als Folge der Gewichtskraft, die auf die über der Sensorfläche liegenden Flüssigkeitssäule wirkt. Die Übereinstimmung mit Messungen und Beobachtungen bestätigt die Richtigkeit des Modells. Dieser so erzeugte Druck heißt auch Schweredruck.

Daraus ergibt sich sofort eine Möglichkeit zur Druckmessung, das U-Rohr-Manometer.

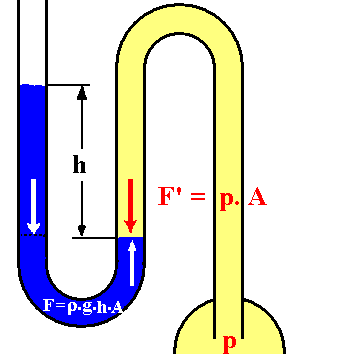Abb. 5: U-Rohr-Manometer. Die Manometerflüssigkeit (dunkel) steigt so hoch, bis KGG zwischen Schweredruck ρ·g·h und zu messendem Druck p (hell) entsteht.

Entscheidend ist hier das KGG an der Trennfläche zwischen Manometerflüssigkeit und Innenraum: Die eingeschlossene Flüssigkeit (gelb) übt in Abb. 5 eine Kraft vom Betrag F' = p·A nach unten aus, die Manometerflüssigkeit (blau) mit der Steighöhe h drückt dagegen mit einer Kraft F = ρ·g·h·A. Bei KGG (F = F') gilt also p = ρ·g·h, wobei ρ die Dichte der Manometerflüssigkeit ist. Die Steighöhe h im U-Rohr ist also ein Maß für den Druck p.

Früher hat man als Manometer-Flüssigkeit häufig Quecksilber verwendet, weil es eine hohe Dichte (ρ = 13,6 kg/dm³) hat (13,6 mal größer als die von Wasser) und deshalb bei relativ geringer Höhe h schon brauchbare Schweredrucke anzeigt. Heute wird Quecksilber lieber vermieden, weil seine Dämpfe (auch die in Leuchtstoffröhren) giftig sind. Früher hat man einfach die Höhe der Quecksilbersäule als Maß für den Druck genommen und ihm die Einheit 1 mm Quecksilber(säule) = 1 Torr gegeben. Für den mittleren Luftdruck auf Meereshöhe ergibt sich dann 760 mm Quecksilber = 760 Torr. Torr ist nach dem Italiener Torricelli genannt, der im 17. Jahrhundert parallel zu Pascal und Otto von Guericke den Luftdruck entdeckt und erforscht hatte. Ärzte denken deshalb beim Blutdruck in Torr, auch wenn auch sie längst modernste elektronische Druckmesser verwenden.

Pascal zeigte den Schweredruck sehr eindrucksvoll mit einem Weinfass. Mit einer Pascal'schen Druckdose (Abb. 9) lässt sich der Versuch nachbilden.

Musteraufgabe: Der normale (durchschnittliche) Luftdruck auf Meereshöhe beträgt 1013 HPa. Wie hoch müsste die Wassersäule in einem dafür geeigneten U-Rohr-Manometer sein? Wie bei Quecksilber als Manometerflüssigkeit? Geg.: p = 1013 HPa = 1013·100 N/m2 = 1,013·105 N/m2 ρw = 1000 kg/m3, ρHg = 13600 kg/m3 = 13,6 · ρw . Ges. h Lösung: p = ρw·g·h => h = p/ρw · g = 1,013·105 N/m2 / (1000 kg/m3·9,81 N/kg) = 1,013/9,81 ·102 N/m2·m3/kg · kg/N = 1,013/9,81·102 m = 10,3 m also reichlich unhandlich! Bei Hg ergibt sich 1/13,6 davon, also h = 0,76 m = 760 mm.

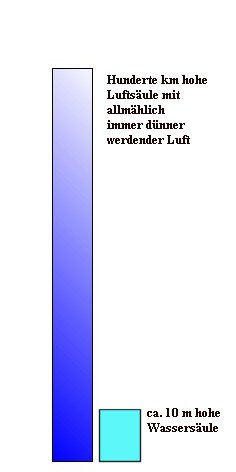Abb. 6: Schweredruck einer Luftsäule auf Meereshöhe verglichen mit dem einer Wassersäule (türkis) Der Luftdruck auf Meereshöhe beträgt ca. 1000 hPa.

Aufgabe zu Abb. 6:

a) Der Luftdruck auf Meereshöhe unter Normalbedingungen ist 1013 HPa. Passen dazu näherungsweise die Angaben von Abb. 6 ?

b) Die Wassersäule soll eine Grundfläche von 1 cm² haben. Welche Gewichtskraft wirkt am Boden und welche Masse hat die Wassersäule?

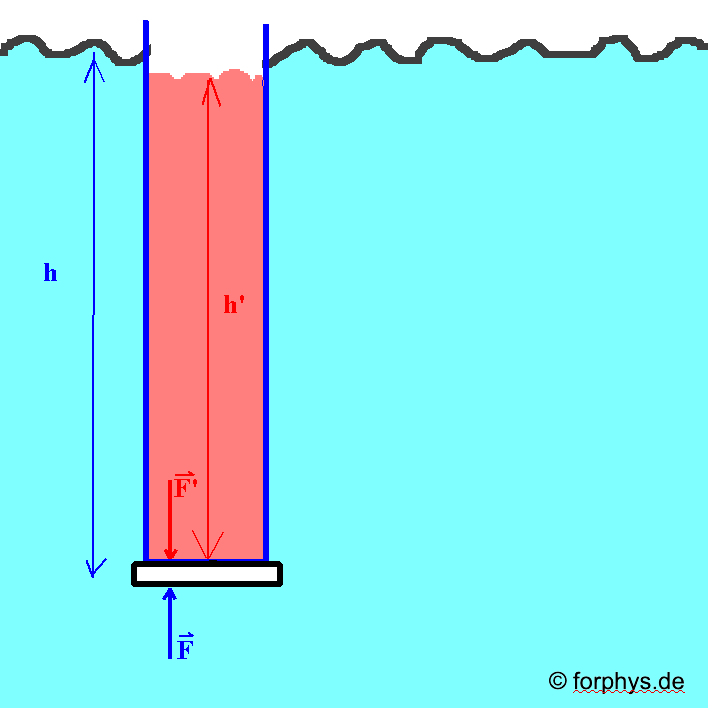Abb. 7: Demonstration des Schweredrucks: Der Schweredruck in einer Wassertiefe h erzeugt eine Kraft F, die ein Diaglas gegen den unten offenen Standzylinder drückt. Du kannst vorsichtig gefärbtes Wasser in den Zylinder einfüllen (hier rot) ohne dass das Diaglas abfällt. Das geschieht erst kurz bevor die Höhe h erreicht ist. Welche Rolle spielt das Gewicht vom Diaglas?

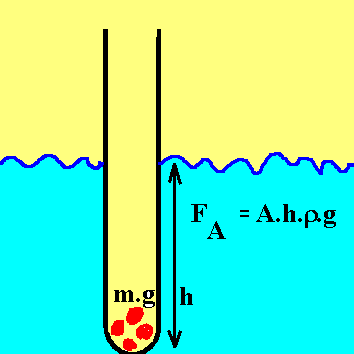Abb. 8: Prinzip eines Aräometers zur Dichtebestimmung der Flüssigkeit. Das mit Bleikörnern (Bleischrot) beschwerte Reagenzglas taucht so tief ein, bis KGG zwischen Gewichtskraft und Auftriebskraft erreicht ist.

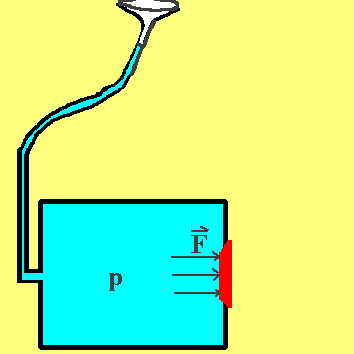Abb. 9: Pascal'sche Druckdose. Eine Teedose mit Deckel ist mit Steigrohr und Trichter versehen. Sie ist mit Wasser gefüllt. Überschreitet die Wassersäule im Füllschlauch eine bestimmte Höhe, erzeugt der Schweredruck eine so hohe Kraft F, dass der Deckel abgesprengt wird.

Eine Überlegung, fast ohne Rechnung:

Zwei nicht mischbare Flüssigkeiten unterschiedlicher Dichte ρ₁ und ρ₂ sind in ein U-Rohr einheitlicher Querschnittsfläche A gefüllt, z.B. Öl und Wasser.

Es gibt eine Trennfläche zwischen beiden Flüssigkeiten: Wir wollen sie die Gleichgewichtsfläche nennen, weil dort Kräftegleichgewicht herrscht zwischen den Gewichtskräften auf die Flüssigkeitssäulen, die auf beiden Seiten oberhalb dieser Gleichgewichtsfläche stehen. Die beiden Höhen der Flüssigkeitssäulen seien H und h. Die Flüssigkeit unterhalb der Gleichgewichtsfläche hat einheitliche Dichte und spielt deshalb keine Rolle.

Welche Höhe überwiegt? Die Masse m einer Säule hängt ab von der jeweiligen Dichte und dem Volumen, also von ρ₁·A·H bzw. ρ₂·A·h. (Beachte: Die Gewichtskraft hat den Betrag G = m·g mit dem Ortsfaktor g). Bei gleicher Querschnittsfläche A muss also gelten: ρ₁·H = ρ₂·h. Zur größeren Dichte gehört offenbar die geringere Höhe h. Bei einer vorgegebenen Höhe der Flüssigkeitssäule lässt sich die andere damit leicht berechnen.

Öl ( ρ₁ = 0,81 g/cm³) hat eine geringere Dichte als Wasser ( ρ₂ = 1 g/cm³). Welche Flüssigkeitssäule steht also höher über der Gleichgewichtsfläche? Die Wassersäule habe eine Höhe von 8,1 cm. Wie hoch ist dann die Ölsäule?

Aufgabe: In manchen Schulbüchern wird ein eindrucksvolles Experiment besprochen: Ein Blatt einer Zeitung wird auf der Tischplatte ausgebreitet. Zwischen Zeitung und Tischplatte wird ein Lineal gesteckt. Dann wird die Zeitung glatt gestrichen. Ein Handkanten- oder Hammerschlag auf das überstehende Ende des Lineals führt zum Bruch des Lineals, obwohl das scheinbar am anderen Ende nicht festgehalten wird. Man findet in verschiedenen Büchern 3 Erklärungen:

(1) Über der Zeitung herrscht der Luftdruck, der bei der großen Fläche des Zeitungsblatts zu einer sehr großen Kraft führt (bei p = 1000 HPa und 1 m² Fläche rechnet man mit 100 000 N).

(2) Würde das Ende des Lineals hochschnellen, wobei es die Zeitung mitnimmt, müsste ein großes Luftvolumen verdrängt werden. Wirbel in der Luft und damit großer Luftwiderstand oder - nach einer anderen Erklärung - die Trägheit der zu verdrängenden Luft verhindern dieses Hochschnellen.

(3) Die Zeitung wird durch elektrische Kräfte auf der Tischplatte festgehalten. Dafür spricht ein besonders gutes Gelingen, wenn man das Zeitungspapier vorher bügelt und wenn der Tisch eine Kunststoffoberfläche hat. Auch am leisen Knistern verraten sich elektrische Ladungen, wenn man das Blatt vorsichtig anhebt.

Überlege, welche der Möglichkeiten dir einsichtig erscheint. Warum kommt Möglichkeit (1) überhaupt nicht in Frage?

.

( Mai 2015; nach Hinweis von Herrn Sturde korrigiert )

(April 2018; Überlegung zum U-Rohr mit zwei Flüssigkeiten ergänzt; einige Formulierungen präzisiert)