. Startseite FORPHYS .

Physik für Schülerinnen und Schüler Auftrieb © H. Hübel Würzburg 2013

Empfohlene Glossarthemen: Druck Dichte Temperatur

Glossar Physik für Schülerinnen und Schüler

Impres-sum

1. Druck als Spannungszustand - "Kraft macht Druck" / "Druck macht Kraft"

(siehe Kapitel "Druck")

Nimmt man einen aufgeblasenen Luftballon und presst ihn mit äußeren Kräften zusammen, so entsteht in der eingeschlossenen Luft ein Spannungszustand, erkennbar daran, dass es immer schwerer wird, ihn weiter zusammenzupressen, oder dass Teile des Luftballons "ausweichen". Bei extrem starken äußeren Kräften kann der Spannungszustand in der eingeschlossenen Luft sogar dazu führen, dass der Luftballon platzt.

Genauso entsteht ein Spannungszustand im eingeschlossenen Gas oder einer eingeschlossenen Flüssigkeit in einer Spritze, wenn man bei geschlossener Austrittsöffnung auf den Stempel drückt. Allgemein nennt man das zylindrische Gefäß der Spritze eben Zylinder; der Stempel heißt oft auch Kolben, besonders beim PKW sind Zylinder und Kolben die Grundlage für die Funktion des Motors und von Bremsen.

Ein Druck p entsteht häufig, indem eine Kraft F senkrecht auf eine Fläche A ausgeübt wird. Dann gilt:

Umgekehrt gilt auch:

Danach entsteht in einem Gefäß, in dem ein Druck p herrscht, auf jedes ebene Flächenstück A eine Kraft, die senkrecht auf das Flächenstück wirkt und einen Betrag gemäß /F/  = p·A hat.

Beachte: Der Druck p ist nicht "Kraft pro Fläche", wie manchmal behauptet wird, denn die Kraft ist ja ein Vektor, und in die Druckformel geht nur der Betrag der Kraft ein. Deshalb hat der Druck auch keine Richtung wie eine Kraft. Der Druck p kennzeichnet nur den Spannungszustand, der in dem Gas oder der Flüssigkeit herrscht. Für die Einheit des Drucks gilt:

[p] = 1 N/m² = 1 Pa

Bringt man einen Drucksensor mit einer Membranfläche A in eine Flüssigkeit oder ein Gas, dann entsteht durch die über der Sensormembran stehende Flüssigkeits- oder Gassäule ein Schweredruck p. Der Druck in einer Tiefe h, wenn also die über der Messstelle liegende Flüssigkeits- oder Gassäule h ist, ist proportional zu dieser Höhe h. Er hängt auch von der Dichte ρ der Flüssigkeit ab. (Gleiches gilt für Gase). Wenn die Dichte ρ konstant ist, ergibt sich für den Schweredruck:

2.  Der Auftrieb

Tauchen ist gar nicht so einfach. Du musst dich schon sehr anstrengen, um im Schwimmbecken 2 m nach unten zu gelangen. Einen Fussball oder gar Wasserball unter Wasser zu drücken, ist fast unmöglich. Eine beträchtliche Kraft drückt dich bzw. den Ball nach oben: die Auftriebskraft. Welche Gesetzmäßigkeit gilt für sie? Wie kommt sie zustande?

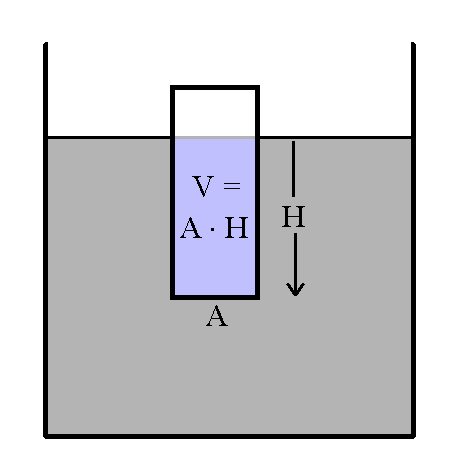
Abb. 1: Eintauchtiefe H und Querschnittsfläche A

Die Auftriebskraft lässt sich messen. Dabei wird ein regelmäßig geformter, nicht zu leichter Körper, z.B. ein Zylinder aus Aluminium, um unterschiedliche Strecken H in Wasser eingetaucht. Die Strecke H wird Eintauchtiefe genannt. Ein Kraftmesser zeigt jeweils eine Kraft an, die geringer als die Gewichtskraft auf den Körper ist. Der scheinbare Gewichtsverlust ist gerade die Auftriebskraft F_A. Versuche zeigen:

1. F_A ist proportional zur Eintauchtiefe H.
2. F_A ist proportional zur Dichte ρ_Fl der Flüssigkeit (!).
3. F_A ist proportional zur Querschnittsfläche A.
4. F_A ist proportional zum Ortsfaktor g.

Es gilt also:

A·H ist gerade der Teil des Volumens des Körpers, der in die Flüssigkeit eintaucht. Er verdrängt dabei genau dieses Flüssigkeitsvolumen, d.h. die Auftriebskraft F_A = ρ_Fl ·g·A·H = ρ_Fl ·V·g = m_Fl · g ist die Gewichtskraft, die auf das vom eintauchenden Körper verdrängte Flüssigkeitsvolumen V wirkt.

Diesen Satz musst du dir merken, nicht die Formel darüber.

Aber wie soll man das verstehen: Die Auftriebskraft ist eine Kraft nach oben, aber sie hat den gleichen Betrag wie eine nach unten gerichtete Gewichtskraft?

Mit dem Schweredruck lässt sich das leicht erklären: Nehmen wir an, ein Zylinder taucht so ins Wasser ein, dass sich seine Deckfläche gerade an der Wasseroberfläche befindet. An seiner Bodenfläche, in der Tiefe H, herrscht der Schweredruck p = ρ_Fl ·g·H. Wie auf jede Fläche wirkt auch senkrecht auf die Bodenfläche A des eintauchenden Körpers, also nach oben, eine Kraft F = p · A = ρ_Fl ·g·H·A . Das ist gerade die Auftriebskraft! Sie kommt durch den Schweredruck der umgebenden Flüssigkeit zustande. Auch Abb. 7 von Kap. Druck zeigt dies (Demonstration des Schweredrucks).

Aber, wenn der Zylinder tiefer ins Wasser eintaucht, so dass er ganz bedeckt ist? Dann wirkt doch auch eine Kraft senkrecht auf die Deckfläche, nach unten! Wie ergibt sich aus den beiden Kräften die Auftriebskraft? An der Deckfläche, in der Tiefe h₁, herrscht dann der Druck p₁. Es entsteht eine Kraft F₁ senkrecht auf die Deckfläche A nach unten. An der Bodenfläche, in der Tiefe h₂, h₂ herrscht der Druck p₂. Es entsteht hier eine Kraft F₂ senkrecht auf die Bodenfläche A nach oben. Weil in der größeren Tiefe h₂ der Druck p₂ größer ist als p₁, überwiegt auch F₂ gegenüber F₁. Es entsteht eine Kraft mit dem Betrag F₂ – F₁ nach oben, eben die Auftriebskraft F_A. Es hat sich fast nichts geändert gegenüber den vorangehenden Überlegungen. Nur ist jetzt die Auftriebskraft F_A die Differenz von zwei Kräften!

Dass das die Auftriebskraft FA ist, lässt sich auch beweisen: Es gilt: (1) p1 = ρFl ·g· h1 , und damit wegen F1 = p1 · A : (1') F1 = ρFl · g · h1 · A und auch p2 = ρFl ·g· h2 , und damit wegen F2 = p2 · A : (2') F2 = ρFl · g · h2 · A Ganz klar, weil h2 > h1 , wirkt in der größeren Tiefe h2 die größere Kraft F2 . Für den Betrag der Auftriebskraft gilt dann: FA = F2 - F1= ρFl· g · h2 · A - ρFl · g · h1 · A = ρFl ·g · A · (h2 - h1). Hier wurden die gemeinsamen Faktoren ausgeklammert. h2 - h1 ist aber gerade die Höhe H des Zylinders. Wir haben also erhalten: FA = ρFl · g · A · H = ρFl · g · V = mFl · g . Der Index Fl zeigt es: Das ist die Gewichtskraft, die auf das vom Zylinder verdrängte Flüssigkeitsvolumen V wirkt, wie es behauptet wird.

Wenn du eine Auftriebskraft berechnen möchtest, musst du also herausfinden, welches Flüssigkeitsvolumen vom Körper verdrängt wird. Dann berechnest du dessen Masse m_Fl und daraus mit dem Ortsfaktor g die Gewichtskraft, die auf die vom Körper verdrängte Flüssigkeit wirkt. Sie ist von gleichem Betrag wie die Auftriebskraft. Aber: Nur in seltenen Fällen wirst du die Auftriebskraft aus der Differenz der Druckkräfte F₂ und F₁ bestimmen.

Musteraufgabe: Ein Eisenquader (Dichte ρE = 7850 kg/m3) mit dem Volumen V = 2,0 dm3 taucht ganz in Wasser ein (Dichte ρFl = 1000 kg/m3). Berechne die Gewichtskraft, die auf ihn wirkt, und die scheinbare Gewichtskraft, wenn er ganz in das Wasser eingetaucht ist. Geg.: ρE = 7850 kg/m3, ρFl = 1000 kg/m3 V = 2,0 dm3 = 0,0020 m3; (geschickte Leute wandeln gleich bei den gegebenen Größen in "vernünftige" Einheiten - hier m3 - um. Ges.: FG und FG - FA Lösung: FG = mE · g = ρE · V · g = 7850 kg/m3 · 0,0020 m3· 10 N/kg = 7850 · 0,02 N = 157 N (Sowohl im Nenner als auch im Zähler stehen m3und kg; damit lässt sich also kürzen). Wenn der Eisenquader ganz in Wasser eingetaucht ist, gleicht das verdrängte Flüssigkeitsvolumen dem Quadervolumen V. Statt der Eisendichte ist jetzt die Dichte des Wassers zu berücksichtigen. Also: FA = mFl · g = ρFl · V · g = 1000 kg/m3 · 0,0020 m3 · 10 N/kg = 20 N. (Klar: 2 dm3 sind 2 Liter mit je 1 kg Masse, also erfahren sie bei uns ca. 20 N Gewichtskraft!) Antwortsatz: Auf den Körper wirkt die Gewichtskraft 157 N, ganz eingetaucht aber nur die scheinbare Gewichtskraft von 137 N.

Genauso gibt es eine Auftriebskraft in einem Gas. Als Dichte ist jetzt die Dichte des umgebenden Gases einzusetzen. Wegen der kleineren Dichte ρ ist der Auftrieb in Luft i.A. deutlich geringer als in Flüssigkeiten.

Der Ball ließ sich so schwer unter Wasser drücken, weil er mit seinem großen Volumen viel Wasser verdrängte. Die Gewichtskraft auf dieses verdrängte Wasser hat gleichen Betrag wie die beträchtliche Auftriebskraft.

Wie tief taucht ein Körper in eine Flüssigkeit ein? Ein in eine Flüssigkeit eintauchender Körper (Länge/Höhe h) hat das Bestreben, Kräftegleichgewicht (KGG) zwischen der Gewichtskraft auf ihn und der Auftriebskraft zu erreichen. Evtl. taucht er nur teilweise in die Flüssigkeit ein (Eintauchtiefe H), gerade so weit, bis die Auftriebskraft auf die verdrängte Flüssigkeit der Gewichtskraft auf den Körper entspricht. Also (bei überall gleicher Querschnittsfläche A des Körpers):

ρ_Fl ·g·A·H = ρ_K ·g·A·h

h ist da bei die Länge/Höhe des Körpers. Es folgt:

(*)           H = h · ρ_K / ρ_Fl.

Bei einem festen Paar von Körper und Flüssigkeit ist das Verhältnis der Dichten konstant. Dann ist die Eintauchtiefe H immer derselbe Prozentsatz der Länge/Höhe h des Körpers.

Abb. 2: Effekt-Lampe. Die Kerze schwimmt in einem hohen, engen Gefäß. Es sorgt dafür, dass die Kerze in aufrechter Position verbleibt und sich nicht etwa querlegt. Es muss darauf geachtet werden, dass die Flamme nur im weiten Teil des Gefäßes brennt. Aufgabe: a) Was kannst du aus (*) für die im Wasser schwimmende Kerze schließen, die langsam abbrennt? Wird das Wasser die Flamme nicht schnell löschen? Gehe dabei von einer zylinderförmigen Kerze aus. b) Setze die Argumentation fort: Wenn das Gewicht der Kerze sinkt, wird die Auftriebskraft ... . Das wird erreicht, indem ... . c) Schätze die Dichte  der Kerze ab, wenn die Länge der Kerze h ≈ 17,5 cm und die Eintauchtiefe H ≈ 16 cm beträgt. d) Warum war dir von vornherein klar, dass die Dichte der Kerze geringer als die des Wassers ist?

Aus der letzten Beziehung ergeben sich eine Reihe von Folgerungen (Abb. 2, 3):

Aus Abb. 1:

1. Falls ρ_K < ρ_Fl wird auch H < h, d.h. der Körper taucht nur teilweise in die Flüssigkeit ein. KGG ist vorzeitig erreicht. Man sagt, der Körper schwimmt auf der Flüssigkeit.

2. Wenn ρ_K = ρ_Fl schwebt der Körper in der Flüssigkeit. Er ist dann ganz von der Flüssigkeit bedeckt (h = H) und bleibt überall in der Flüssigkeit stehen, in jeder Tiefe.

3. Wenn ρ_K > ρ_Fl , lässt sich KGG nicht mehr erzielen. Die Gewichtskraft auf den Körper überwiegt, der Körper sinkt in der Flüssigkeit zu Boden.

4. Wenn ρ_K < ρ_Fl, und wenn der Körper vollständig eingetaucht ist, dann ist die Auftriebskraft von größerem Betrag als die Gewichtskraft (kein KGG). So entsteht eine Kraft, die den Körper noch oben zu bringen versucht: Der Körper steigt. Deswegen schwimmen tote Fische auf der Wasseroberfläche; durch die bei der Verwesung entstehenden Gase steigt ihr Volumen und das der verdrängten Flüssigkeit.

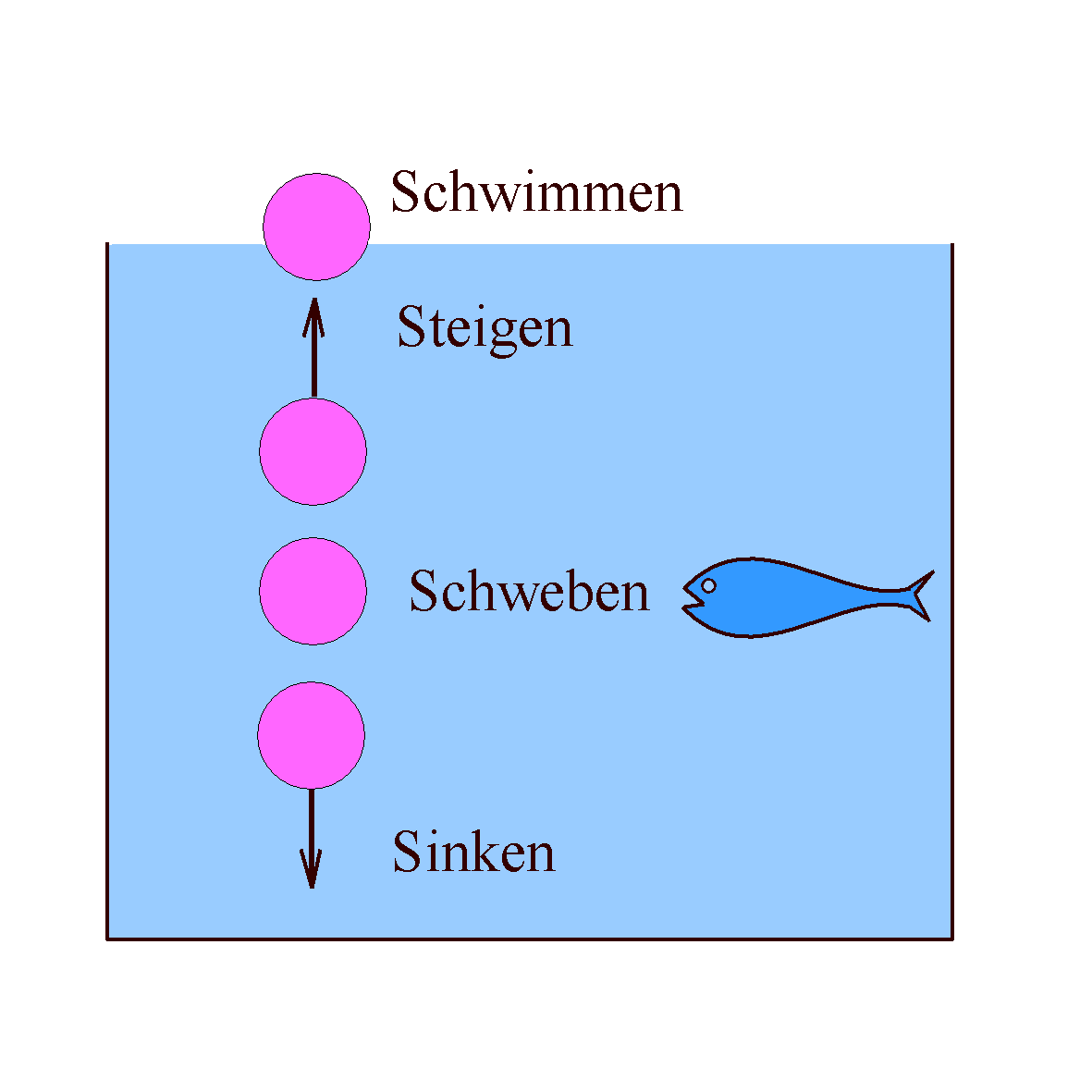Abb. 3: Die Begriffe Schwimmen, Steigen, Schweben, Sinken in der Physik. Ein Fisch schwebt i.A. im Wasser! In anderen Sprachen haben es Schüler etwas einfacher. Für das physikalische Schwimmen haben sie oft ein eigenes Wort, z.B. to float im Englischen oder flutuar im Portugiesischen im Unterschied zum sportlichen Schwimmen mit to swim bzw. nadar.

Nach dieser physikalischen Bezeichnungsweise schweben lebende Fische in der Regel im Wasser. Auf keinen Fall "schwimmen" sie in diesem Sinn, wie man umgangssprachlich sagt. Mit Hilfe der Schwimmblase (mit mehr oder weniger Luft) können sie ihre mittlere Dichte verändern und deshalb im Wasser steigen, schweben oder sinken. Bei Tauchbooten hat man das nachgeahmt. Durch Kammern, die geflutet werden können, oder aus denen mit Hilfe von Pressluft alles Wasser herausgepresst werden kann, lässt sich das scheinbare Gewicht des Tauchboots so verändern, dass seine mittlere Dichte geringfügig um die Dichte von Wasser veränderbar ist. Auf dem Auftrieb beruht auch das Prinzip eines Aräometers zur Dichtemessung (Abb. 7 vom Kapitel Druck).

Schiffe schwimmen nur teilweise eingetaucht auf dem Wasser, weil sie durch ihren bauchigen Rumpf viel Wasser verdrängen. Deshalb entsteht eine große Auftriebskraft. Je schwerer sie beladen werden, desto tiefer tauchen sie, desto größer ist die Auftriebskraft, bis diese schließlich der gestiegenen Gewichtskraft das Gleichgewicht hält.

Abb. 4: Gasgefüllte Luftballons können steigen, weil sie bei relativ geringem Gewicht viel Luft verdrängen und deshalb eine Auftriebskraft in Luft erfahren, die die Gewichtskraft überschreitet. Mit dem Brenner sorgt man für warme Luft, die sich ausdehnt und den Ballon bläht: mit dem zunehmenden Volumen steigt die Auftriebskraft. Wenn mit zunehmender Höhe die Dichte der äußeren Luft abnimmt, sinkt auch die Auftriebskraft: Es stellt sich schließlich KGG ein und die maximale Steighöhe ist erreicht. Wenn der Ballonfahrer Sandsäcke abwirft, sinkt die Gewichtskraft, und die Auftriebskraft reicht wieder aus um den Ballon weiter steigen zu lassen.

Musteraufgabe: Ein Holzquader (Dichte ρK = 0,70 kg/dm3) mit einer Querschnittsfläche A = 60 cm2 und einer Höhe h = 5,0 cm schwimmt teilweise eingetaucht auf einer Wasseroberfläche. Wie tief taucht er ein (Eintauchtiefe H), wenn angenommen wird, dass er nicht kippt? Geg.: ρK = 0,70 kg/dm3, ρFl = 1,0 kg/dm3 A = 60 cm2 h = 5,0 cm Ges.: H Lösung: Je tiefer der Holzquader in das Wasser eintaucht, desto größer ist die Auftriebskraft. Der Holzquader taucht so tief ein, bis KGG zwischen der Gewichtskraft auf ihn und der Auftriebskraft entstanden ist. Dann gilt also ρFl ·g·A·H = ρK ·g·A·h Nach Kürzen: H = ρK / ρFl . h = 0,70 kg/dm3 / 1,0 kg/dm3 . 5,0 cm = 3,5 cm Antwortsatz: Der Holzquader taucht 3,5 cm tief in das Wasser ein, noch 1,5 cm von ihm sind nicht mit Wasser bedeckt.

Auch bei Flugzeugen ermöglicht eine Art von Auftriebskraft das Schweben in der Luft.

Diese ist aber von ganz anderer Art und hängt mit der Umströmung der Tragflächen durch den "Fahrtwind" zusammen ("dynamischer Auftrieb"). Deshalb ist die Form der Tragflächen hier so wichtig.

.

(Oktober 2013)