Vorschlag von von Elitzur und Vaidman (1993), realisiert durch Kwiat, Weinfurter und Zeilinger (1995)

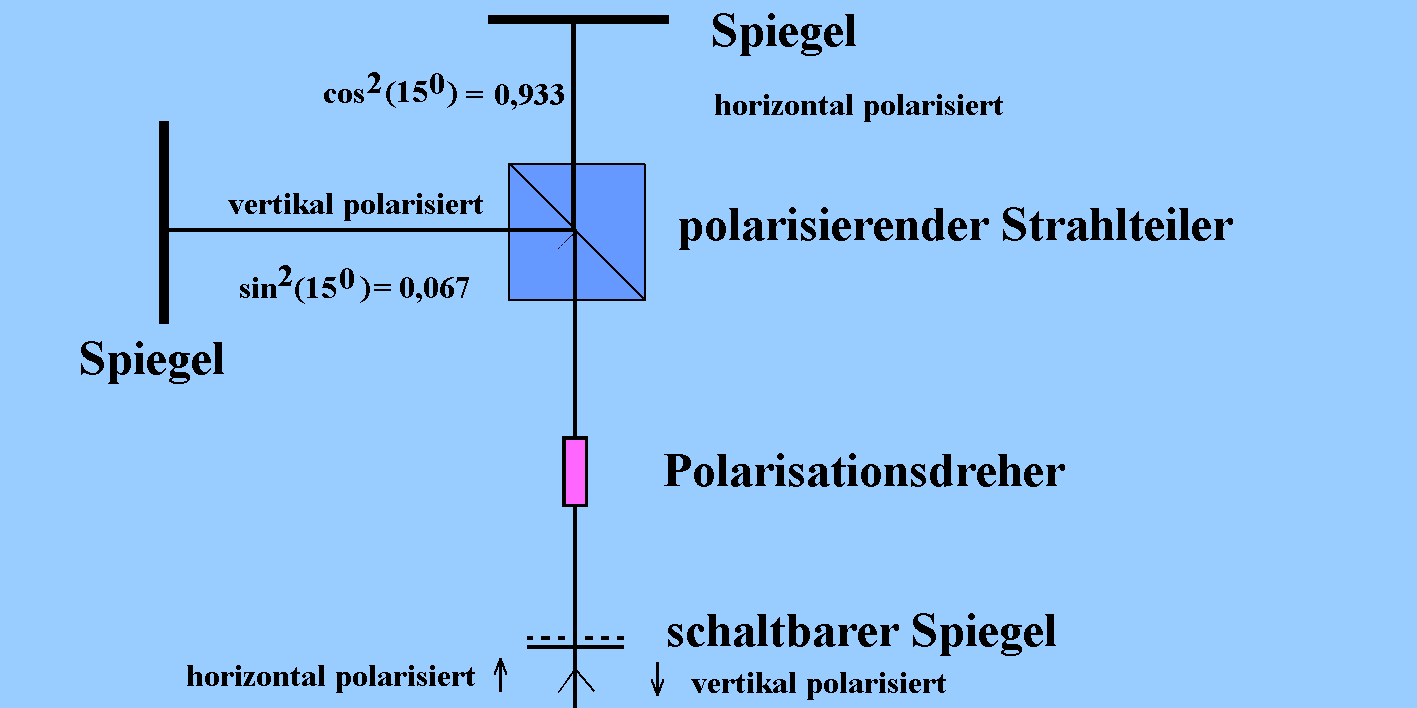
	(1) Die Realisierung des Knaller-Test-Experiments verwendet ein modifiziertes Mach-Zehnder-Interferometer: Horizontal polarisiertes Licht tritt unten ein. Der Polarisationsdreher verändert die Polarsationsrichtung um 150. Das Licht wird dann am polarisierenden Strahlteiler in senkrechte Polarisationsrichtungen aufgespalten, jedoch - bei gleichen Abständen - nach Reflexion hinter dem Strahlteiler wieder phasengerecht vereinigt. Es tritt in den Polarisationsdreher ein, wie es ihn verlassen hat, also um 150 gegenüber der Horizontalen gedreht. Nach 6-maligem Durchlaufen (also 6 x 150 = 900 Polarisationsdrehung) wird der untere Spiegel durchlässig geschaltet: das Photon verlässt die Anordnung mit vertikaler Polarisation.
(Interferenz-Maximum für vertikal polarisiertes Licht, Minimum für horizontal polarisiertes Licht; möglich, weil beide Wege ununterschieden. Die Quanten-Zeno-Anordnung ist unwirksam, da die Polarisationskorrektur "abgeschaltet" ist.)
	(2) Ist jedoch ein Hindernis in einem Arm des Interferometers, also die gefürchtete Super-Bombe oder ein einfacher Knaller, entspricht die Anordnung der Quanten-Zeno-Anordnung: Durch den polarisierenden Strahlteiler wird die Polarisationsdrehung jeweils rückgängig gemacht: Ca. 2/3 des Lichts verlässt die Anordnung nach einem 6-stufigen Zyklus horizontal polarisiert, so wie es eingetreten ist. Der Polarisationsdreher vermindert die Wahrscheinlichkeit, dass ein Photon auf dem "Bombenweg" den Strahlteiler verlässt. 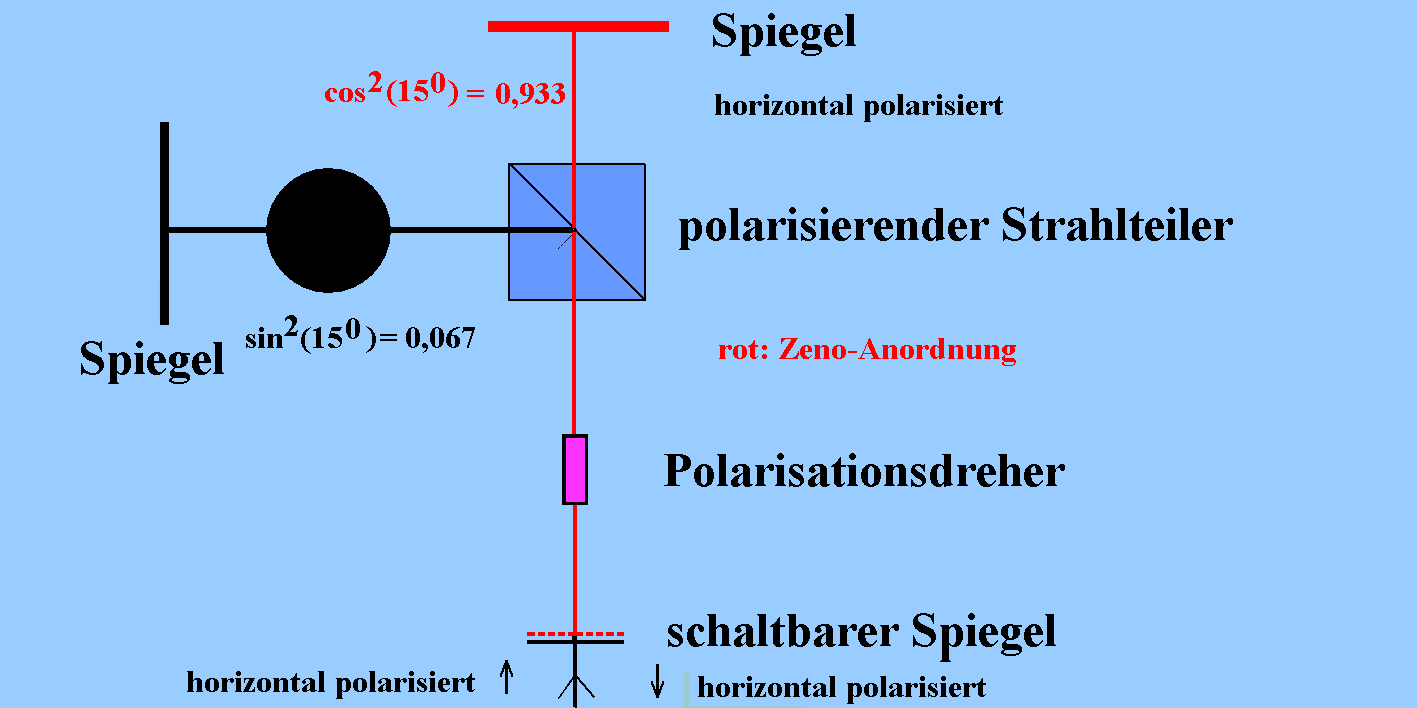An der fehlenden Polarisationsdrehung wird in ca. 2/3 der Fälle erkannt, dass ein Hindernis in einem Zweig des Interferometers steht. (Wahrscheinlichkeit für einmaligen Durchgang mit horizontaler Polarisation: cos2(150) = 0,933, für 6-maligen Durchgang mit horizontaler Polarisation: cos12(150) = 0,66)
Durch die Wahl von mehr Polarisationsdrehern mit jeweils geringerem Drehwinkel kann der Prozentsatz des wieder austretenden Lichts weiter erhöht werden, bzw. der Prozentsatz des Lichts, das auf das Hindernis trifft, vermindert werden. Durch das Hindernis wird die Quanten-Zeno-Anordnung aktiviert. Andernfalls fehlt die Polarisationskorrektur. Man kann es auch so sehen: zwischen den beiden Wegen wird jetzt entschieden: es ist nur ein Weg möglich: deshalb gibt es kein Maximum der Interferenz für vertikal polarisiertes Licht. Durch den Quanten-Zeno-Effekt wird der Lichtweg markiert: austretendes Licht wie eintretendes ist horizontal polarisiert => nur Zeno-Weg. Licht vertikal polarisiert => beide Wege, aber in 1/3 der Fälle blockiert auch das Hindernis den einen Photonen-Weg.

E

1. Durch geschickte Ausnutzung von Quanteneffekten gelingt es in ca. 2/3 aller Fälle ein Hindernis zu entdecken, ohne dass es von einem Photon getroffen wird. 2. Das ist möglich, weil ohne eine Messung (Hindernis) zwischen beiden klassisch denkbaren Wegen durch ein Interferometer nicht entschieden wird. Unterscheidet man aber die beiden klassisch möglichen Wege durch das Hindernis, so wird die Interferenz gelöscht. Durch den Quanten-Zeno-Effekt wird der noch offene Photonen-Weg durch die Polarisation der Photonen "markiert". 3. Der Versuch erläutert auch die Tatsache, dass die Interferenz bereits dann verloren geht, wenn nur die Möglichkeit zu einer Wegmessung besteht, sie nur "angedroht wird", aber tatsächlich nicht durchgeführt wird (das Photon trifft mit einer beträchtlichen Wahrscheinlichkeit nicht die Superbombe, obwohl sie vorhanden ist).